Przekształcenie, obrót i inne transformacje
Niektóre obiekty geometrii mogą być tworzone przez jawne podanie współrzędnych x, y i z w przestrzeni trójwymiarowej. Jednak częściej geometria jest przesuwana do jej położenia końcowego za pomocą transformacji geometrycznych samego obiektu lub jego źródłowego obiektu CoordinateSystem.
Najprostszą transformacją geometryczną jest przekształcenie, które przesuwa obiekt o określoną liczbę jednostek w kierunkach x, y i z.
// create a point at x = 1, y = 2, z = 3
p = Point.ByCoordinates(1, 2, 3);
// translate the point 10 units in the x direction,
// -20 in y, and 50 in z
// p2’s new position is x = 11, y = -18, z = 53
p2 = p.Translate(10, -20, 50);
Mimo że wszystkie obiekty w dodatku Dynamo mogą być przekształcane przez dołączenie metody .Translate do końca nazwy obiektu, bardziej złożone transformacje wymagają przekształcenia obiektu z jednego źródłowego obiektu CoordinateSystem do nowego. Aby na przykład obrócić obiekt o 45 stopni wokół osi x, przekształcilibyśmy obiekt z jego istniejącego obiektu CoordinateSystem bez obrotu do obiektu CoordinateSystem, który został obrócony o 45 stopni wokół osi x za pomocą metody .Transform:
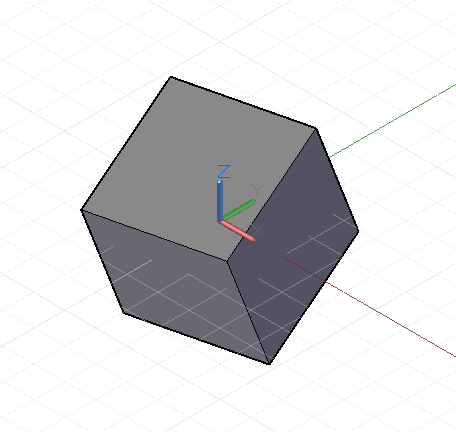
cube = Cuboid.ByLengths(CoordinateSystem.Identity(),
10, 10, 10);
new_cs = CoordinateSystem.Identity();
new_cs2 = new_cs.Rotate(Point.ByCoordinates(0, 0),
Vector.ByCoordinates(1,0,0.5), 25);
// get the existing coordinate system of the cube
old_cs = CoordinateSystem.Identity();
cube2 = cube.Transform(old_cs, new_cs2);
Poza przekształcaniem i obróceniem obiekty CoordinateSystem można również tworzyć skalowane i ścięte. Obiekt CoordinateSystem może być skalowany za pomocą metody .Scale:
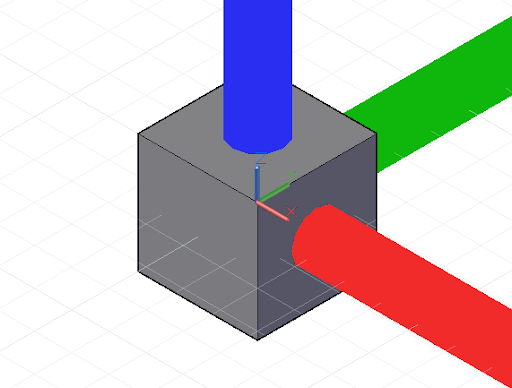
cube = Cuboid.ByLengths(CoordinateSystem.Identity(),
10, 10, 10);
new_cs = CoordinateSystem.Identity();
new_cs2 = new_cs.Scale(20);
old_cs = CoordinateSystem.Identity();
cube2 = cube.Transform(old_cs, new_cs2);
Ścięte obiekty CoordinateSystem tworzy się przez przekazanie wektorów nieortogonalnych do konstruktora CoordinateSystem.
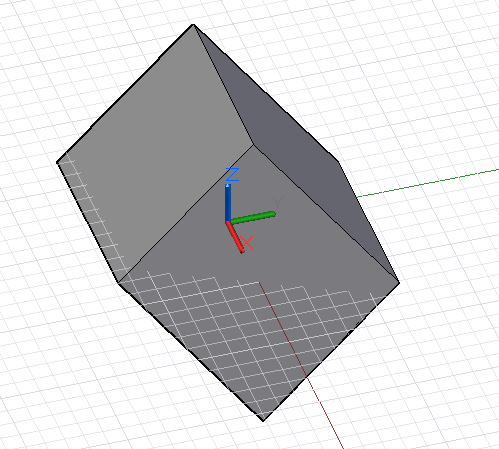
new_cs = CoordinateSystem.ByOriginVectors(
Point.ByCoordinates(0, 0, 0),
Vector.ByCoordinates(-1, -1, 1),
Vector.ByCoordinates(-0.4, 0, 0));
old_cs = CoordinateSystem.Identity();
cube = Cuboid.ByLengths(CoordinateSystem.Identity(),
5, 5, 5);
new_curves = cube.Transform(old_cs, new_cs);
Skalowanie i ścinanie to względnie bardziej skomplikowane transformacje geometryczne niż obrót i przekształcenie, więc nie każdy obiekt Dynamo może je przejść. W poniższej tabeli przedstawiono ogólnie, które obiekty Dynamo mogą mieć niejednorodnie skalowane obiekty CoordinateSystem i ścięte obiekty CoordinateSystem.
| Klasa | Niejednorodnie skalowany obiekt CoordinateSystem | Ścięty obiekt CoordinateSystem |
|---|---|---|
| Łuk | Nie | Nie |
| Krzywa NurbsCurve | Tak | Tak |
| Powierzchnia NurbsSurface | Nie | Nie |
| Okrąg | Nie | Nie |
| Linia | Tak | Tak |
| Płaszczyzna | Nie | Nie |
| Punkt | Tak | Tak |
| Wielobok | Nie | Nie |
| Wypełnienie | Nie | Nie |
| Powierzchnia | Nie | Nie |
| Tekst | Nie | Nie |