Krótka składnia
W bloku kodu dostępnych jest kilka podstawowych metod o krótkiej składni, które znacznie ułatwiają zarządzanie danymi. Podstawy zostały szczegółowo omówione poniżej. Wyjaśniamy też, jak za pomocą tej krótkiej składni można tworzyć dane i stosować do nich zapytania.
| Typ danych | Standard Dynamo | Odpowiednik w bloku kodu |
| Liczby | 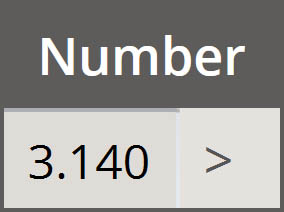 |
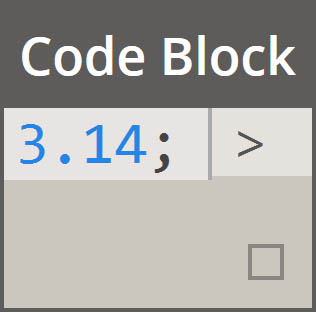 |
| Ciągi | 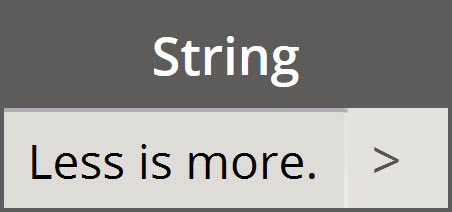 |
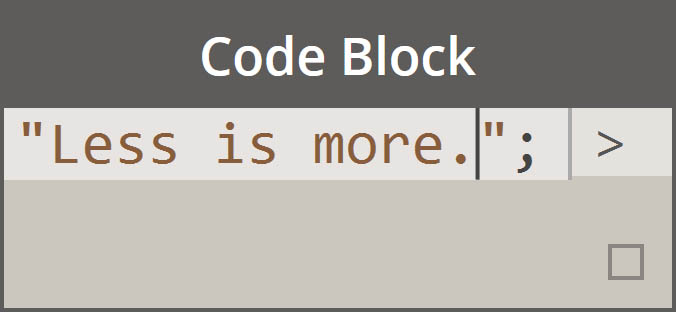 |
| Sekwencje | 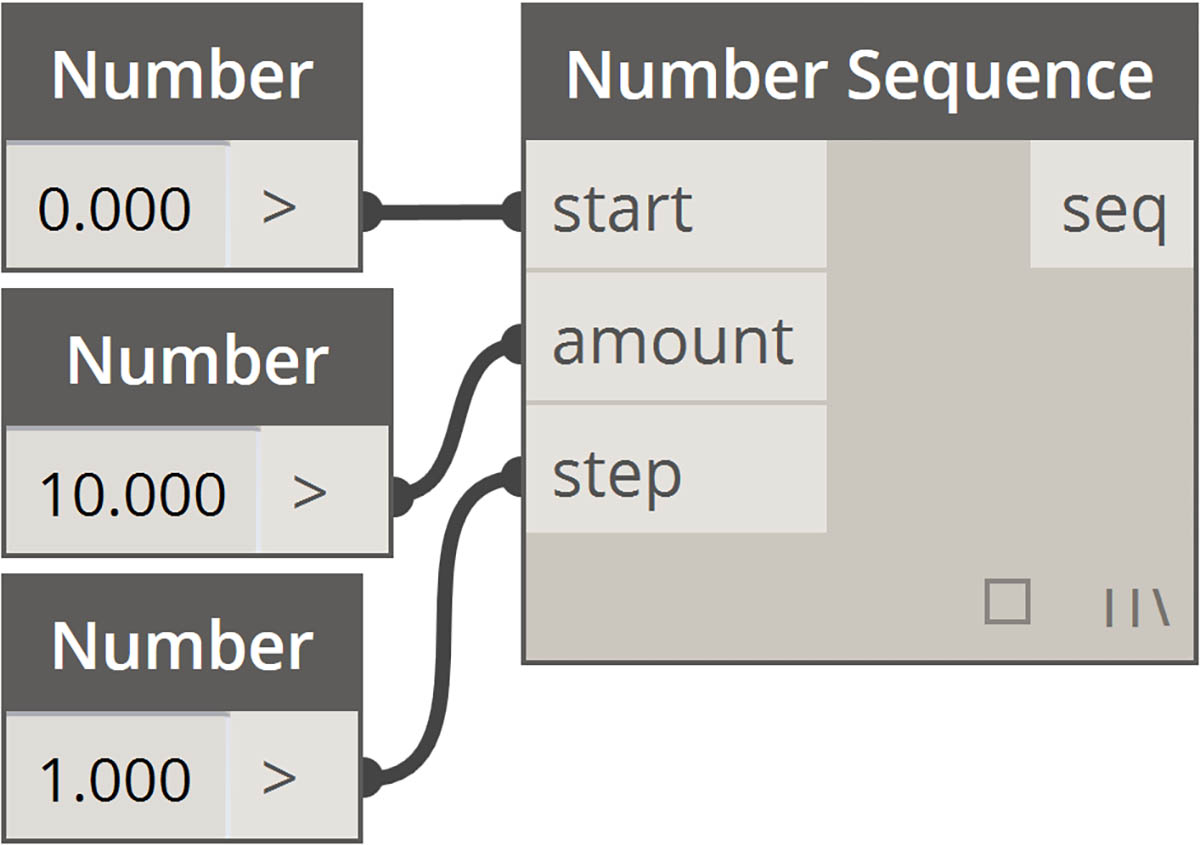 |
 |
| Przedziały | 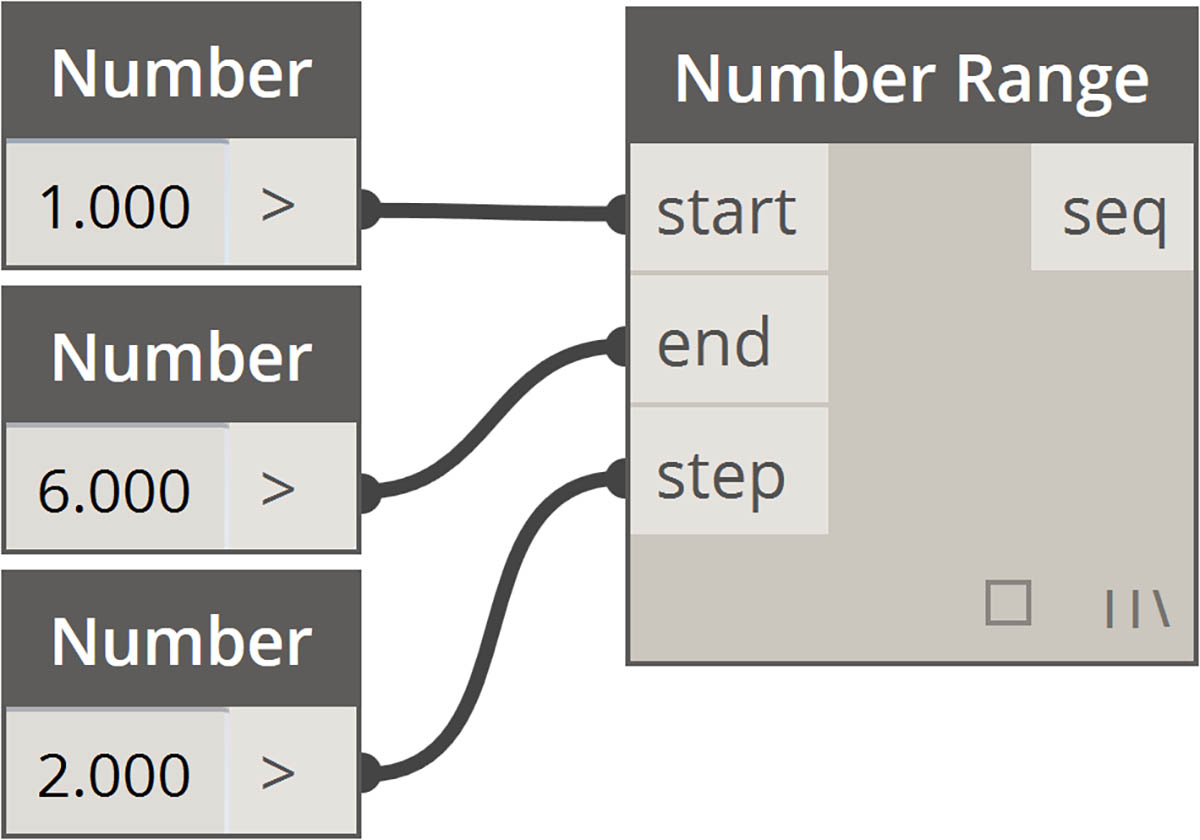 |
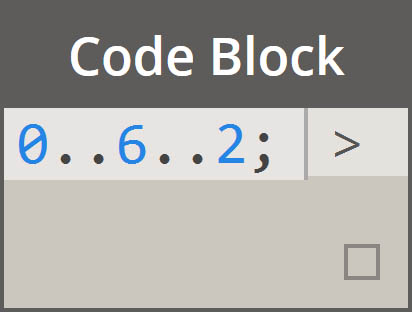 |
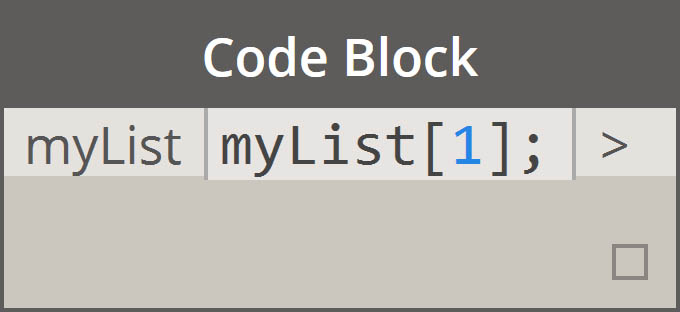
| Pobierz element o indeksie | 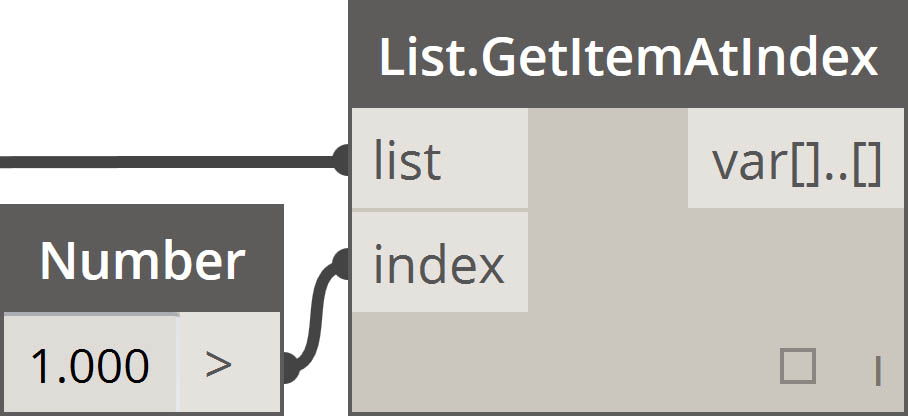 |
 |
| Utwórz listę | 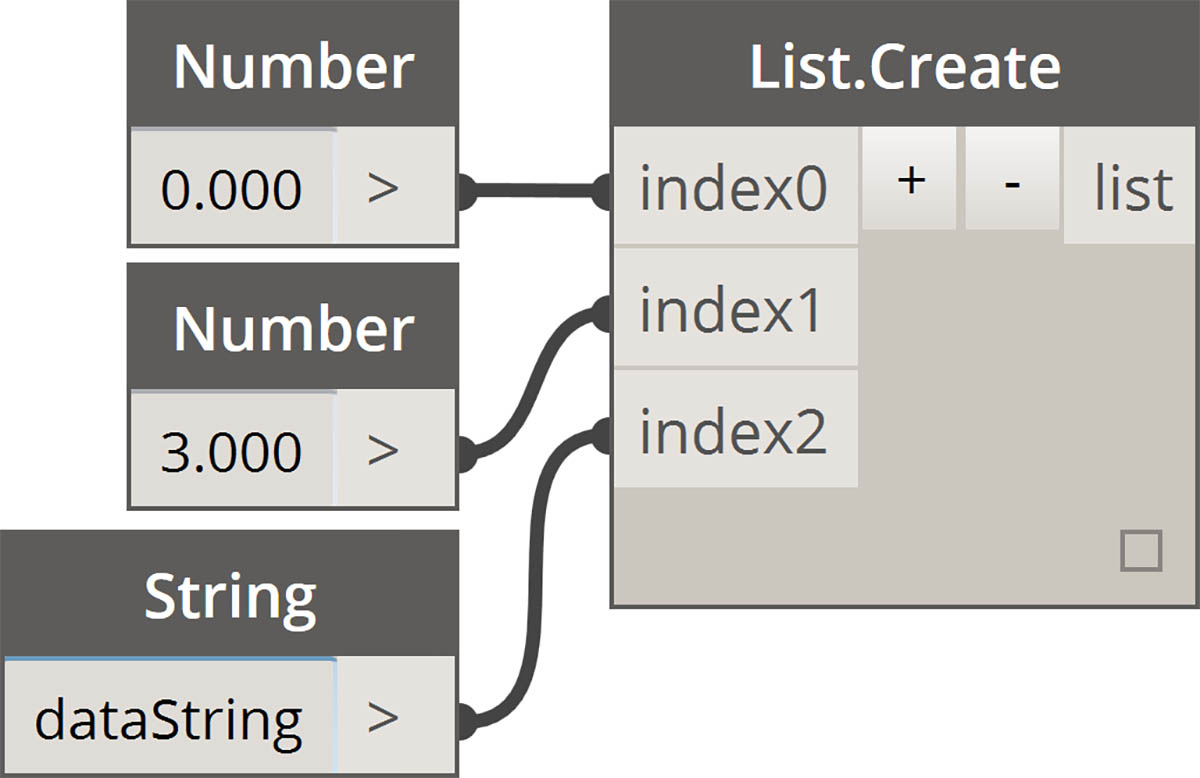 |
 |
| Scal ciągi | 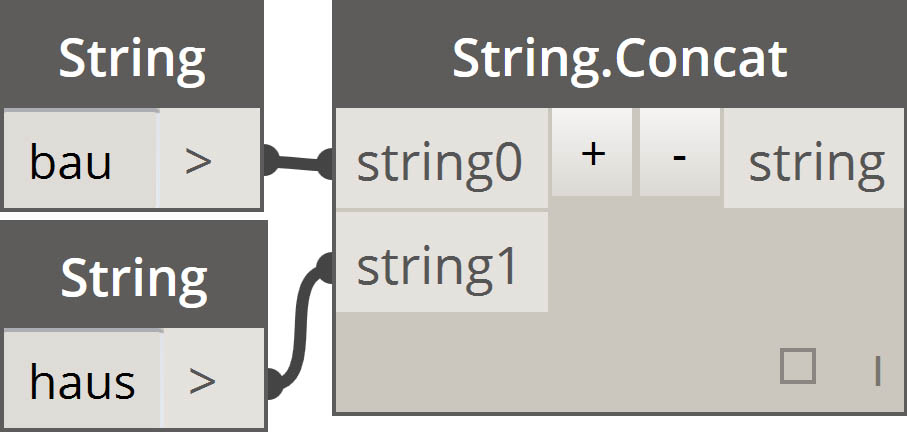 |
 |
| Instrukcje warunkowe | 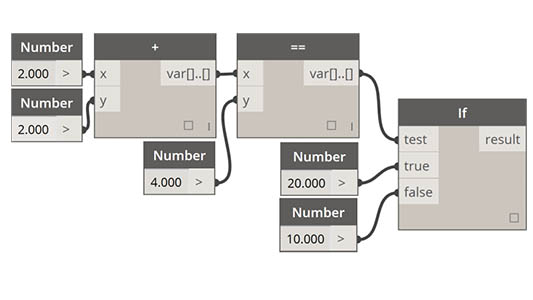 |
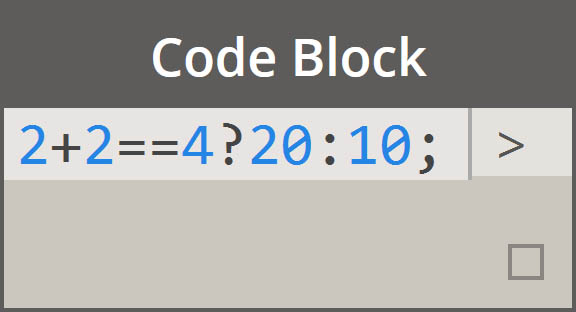 |
Dodatkowa składnia
| Węzły | Odpowiednik w bloku kodu | Uwaga |
|---|---|---|
| Dowolny operator (+, &&, >=, Not itd.) | +, &&, >=, ! itd. | Uwaga: „Not” staje się „!”, ale węzeł nazywa się „Not”, aby odróżnić go od „Factorial” |
| Wartość logiczna True | true; | Uwaga: małe litera |
| Wartość logiczna False | false; | Uwaga: małe litera |
Przedziały
Metoda definiowania zakresów i sekwencji może zostać zredukowana do krótkiej składni. Poniższa ilustracja przedstawia składnię „..”, która umożliwia definiowanie listy danych liczbowych za pomocą bloku kodu. Po zaznajomieniu się z tą notacją tworzenie danych liczbowych jest bardzo wydajnym procesem: 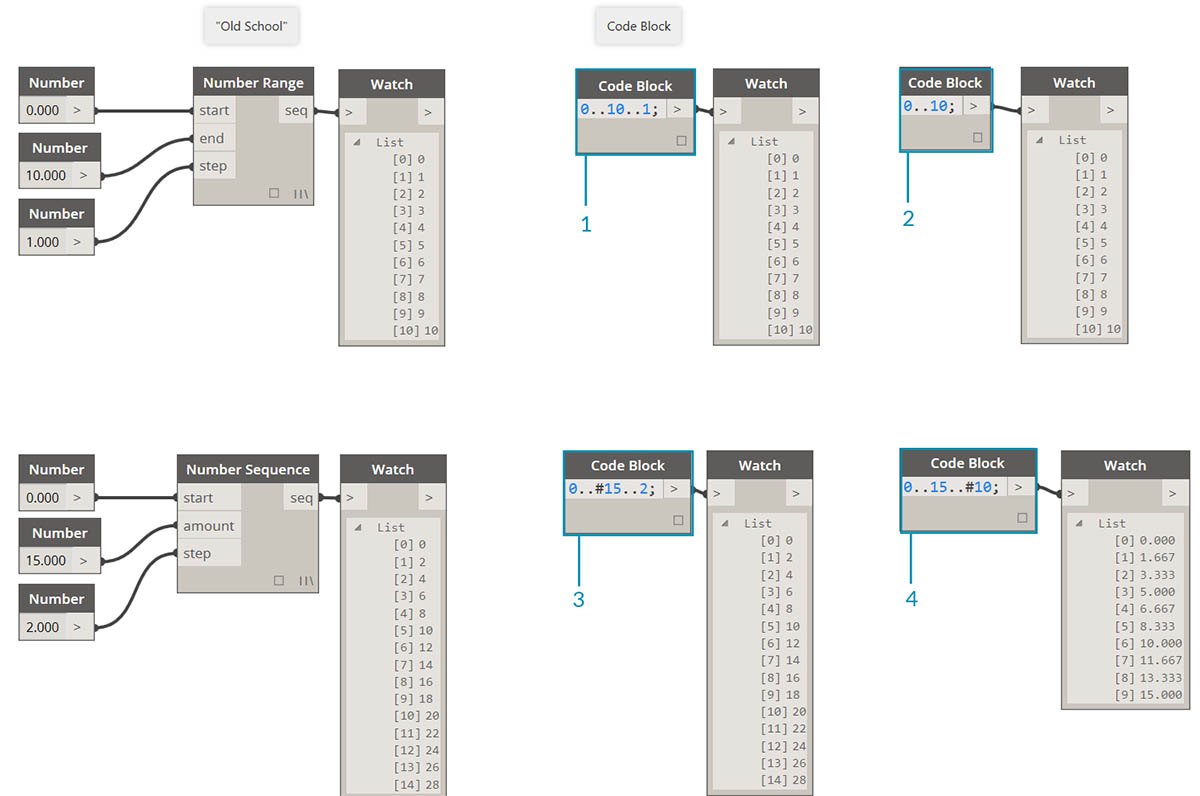
- W tym przykładzie zakres liczb zostaje zastąpiony podstawową składnią bloku kodu definiującą
początek..koniec..rozmiar-kroku;. Liczbowo będzie to:0..10..1;- Uwaga: składnia
0...10..1;jest równoważna składni0..10;. Wielkość kroku równa 1 jest domyślną wartością w krótkiej składni. Dlatego0..10;daje sekwencję od 0 do 10 o kroku 1.- Przykład sekwencji liczb (Number Sequence) jest podobny, ale do ustawienia 15 wartości na liście używamy znaku „#” zamiast listy do 15. W tym przypadku definiujemy:
początek...#liczba-kroków..rozmiar-kroku:. Rzeczywista składnia sekwencji to0...#15..2- Używając znaku „#” z poprzedniego kroku, umieścimy go teraz w części „rozmiar-kroku” składni. Teraz mamy zakres liczb (Number Range) od „początku” do „końca” z ustalonym „rozmiarem-kroku”, co powoduje równomierne rozmieszczenie wartości między dwoma punktami:
początek..koniec..#liczba-kroków
Zakresy zaawansowane
Tworzenie zakresów zaawansowanych pozwala na łatwe korzystanie z listy list. W poniższych przykładach wyodrębniamy zmienną z notacji zakresu głównego i tworzymy inny zakres tej listy. 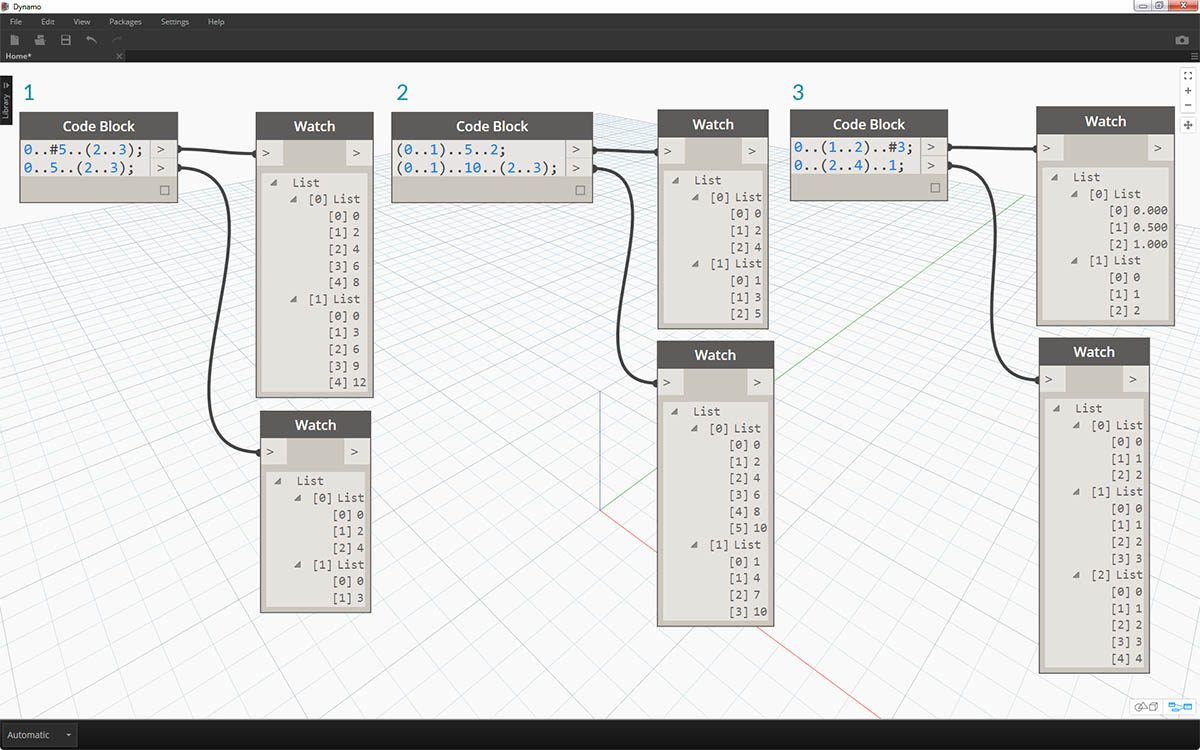
- Tworząc zakresy zagnieżdżone, porównaj notację z „#” z notacją bez tego znaku. Zastosowanie ma ta sama logika co w zakresach podstawowych, choć rozwiązanie jest nieco bardziej złożone.
- Możemy zdefiniować zakres podrzędny w dowolnym miejscu w zakresie głównym i możemy też używać dwóch zakresów podrzędnych.
- Sterując wartością „końca” w zakresie, tworzymy więcej zakresów o różnych długościach.
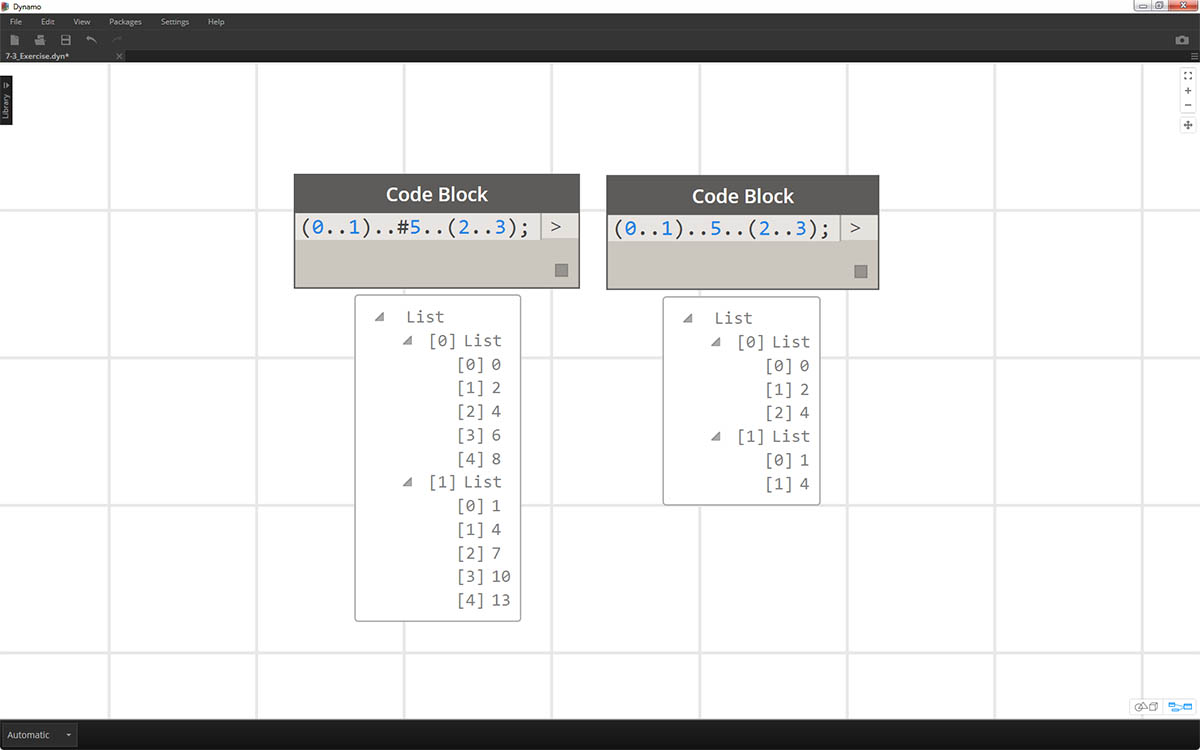
W ramach ćwiczenia logicznego porównaj dwie wersje krótkiej składni i spróbuj przeanalizować, w jaki sposób zakresy podrzędne i notacja „#” wpływają na wynik na wyjściu.
Tworzenie list i pobieranie elementów z listy
Poza tworzeniem list za pomocą krótkiej składni możemy również tworzyć listy na bieżąco. Te listy mogą zawierać szeroki zakres typów elementów i można stosować do nich zapytania (należy pamiętać, że listy to także obiekty). Podsumowując: blok kodu pozwala tworzyć listy za pomocą nawiasów klamrowych i stosować zapytania o elementy z listy za pomocą nawiasów kwadratowych:
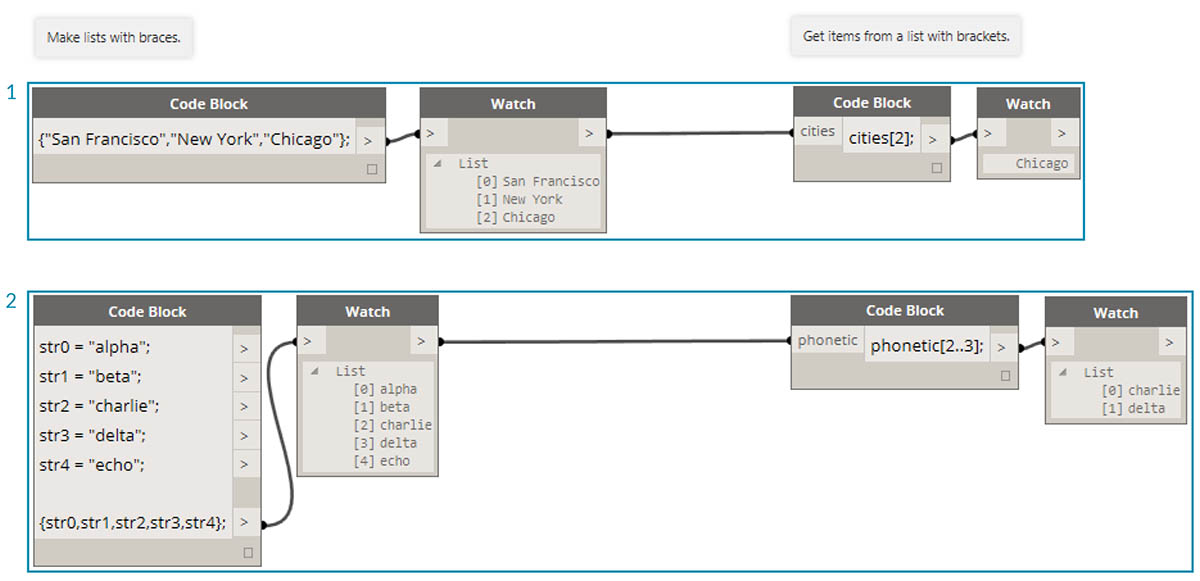
- Szybko twórz listy za pomocą ciągów i stosuj do nich zapytania, korzystając z indeksu elementu.
- Twórz listy ze zmiennymi i stosuj do nich zapytania za pomocą notacji krótkiej składni zakresu.
Zarządzanie z listami zagnieżdżonymi jest podobnym procesem. Pamiętaj o kolejności listy i o korzystaniu z wielu zestawów nawiasów kwadratowych:
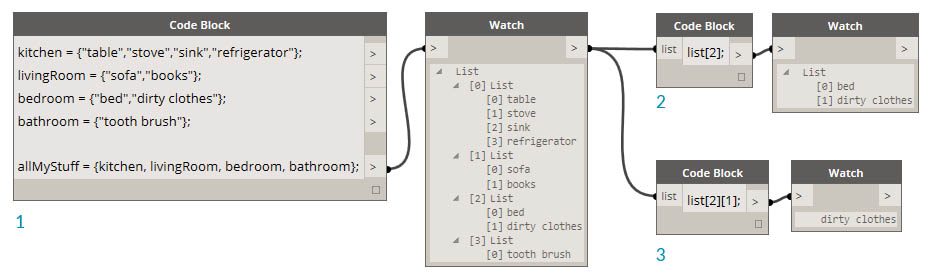
- Zdefiniuj listę list.
- Zastosuj zapytanie do listy za pomocą notacji z jedną parą nawiasów kwadratowych.
- Zastosuj zapytanie do elementu za pomocą notacji z dwiema parami nawiasów kwadratowych.
Ćwiczenie
Pobierz plik przykładowy do tego ćwiczenia (kliknij prawym przyciskiem myszy i wybierz polecenie Zapisz element docelowy jako). Pełna lista plików przykładowych znajduje się w załączniku. Obsolete-Nodes_Sine-Surface.dyn
W tym ćwiczeniu przećwiczymy nowe umiejętności dotyczące krótkiej składni, aby utworzyć „jajowatą” powierzchnię zdefiniowaną przez zakresy i formuły. W trakcie ćwiczenia zwróć uwagę na to, w jaki sposób używane są blok kodu i istniejące węzły Dynamo: blok kodu jest używany do złożonej obsługi danych, natomiast węzły Dynamo są rozmieszczone wizualnie w celu zapewnienia czytelności definicji.
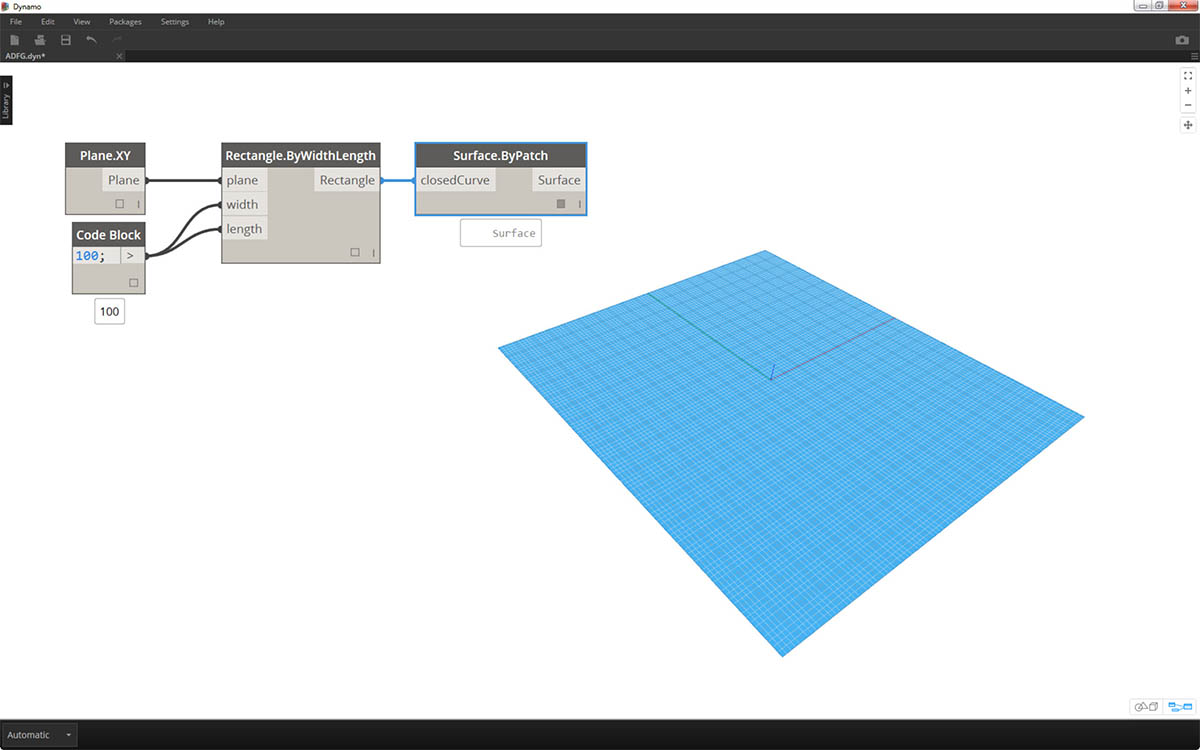
Rozpocznij od utworzenia powierzchni przez połączenie powyższych węzłów. Zamiast używać węzła number do zdefiniowania szerokości i długości, kliknij dwukrotnie obszar rysunku i wpisz
100;w bloku kodu.
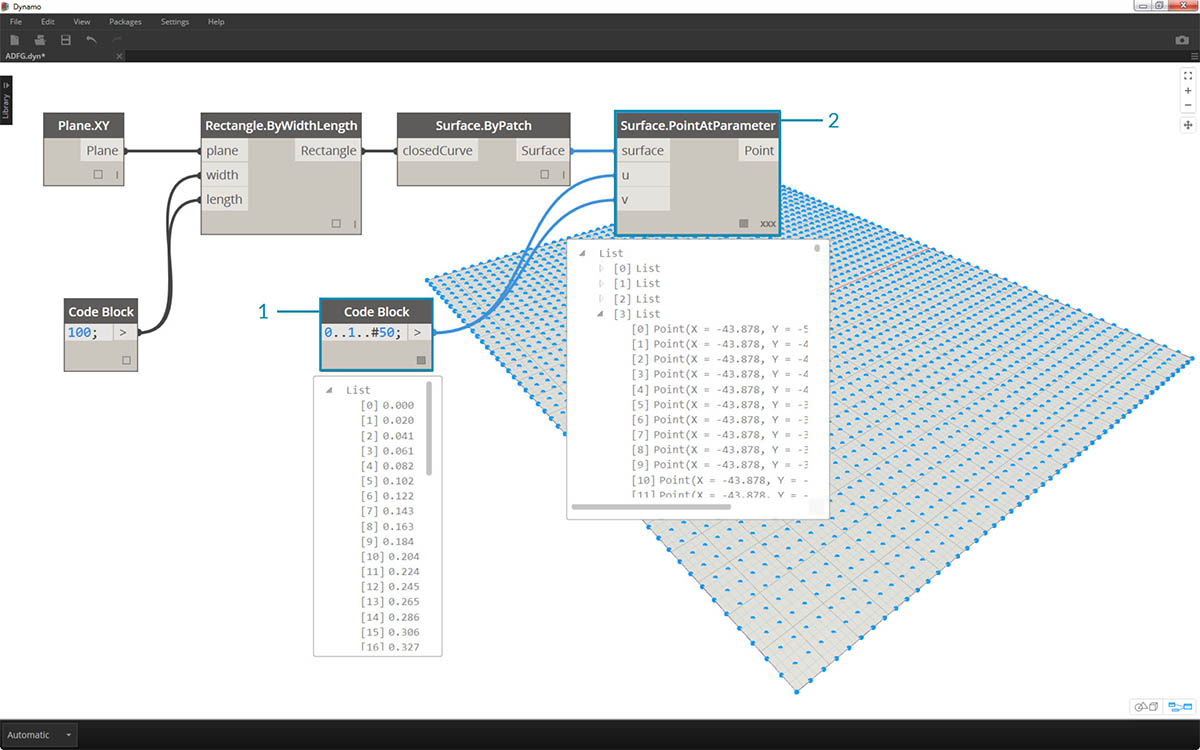
- Zdefiniuj zakres od 0 do 1 z 50 podziałami, wpisując
0..1..#50w bloku kodu.- Połącz ten zakres z węzłem Surface.PointAtParameter, który pobiera wartości u i v z zakresu od 0 do 1 na powierzchni. Pamiętaj, aby zmienić Skratowanie na Iloczyn kartezjański, klikając prawym przyciskiem myszy węzeł Surface.PointAtParameter.
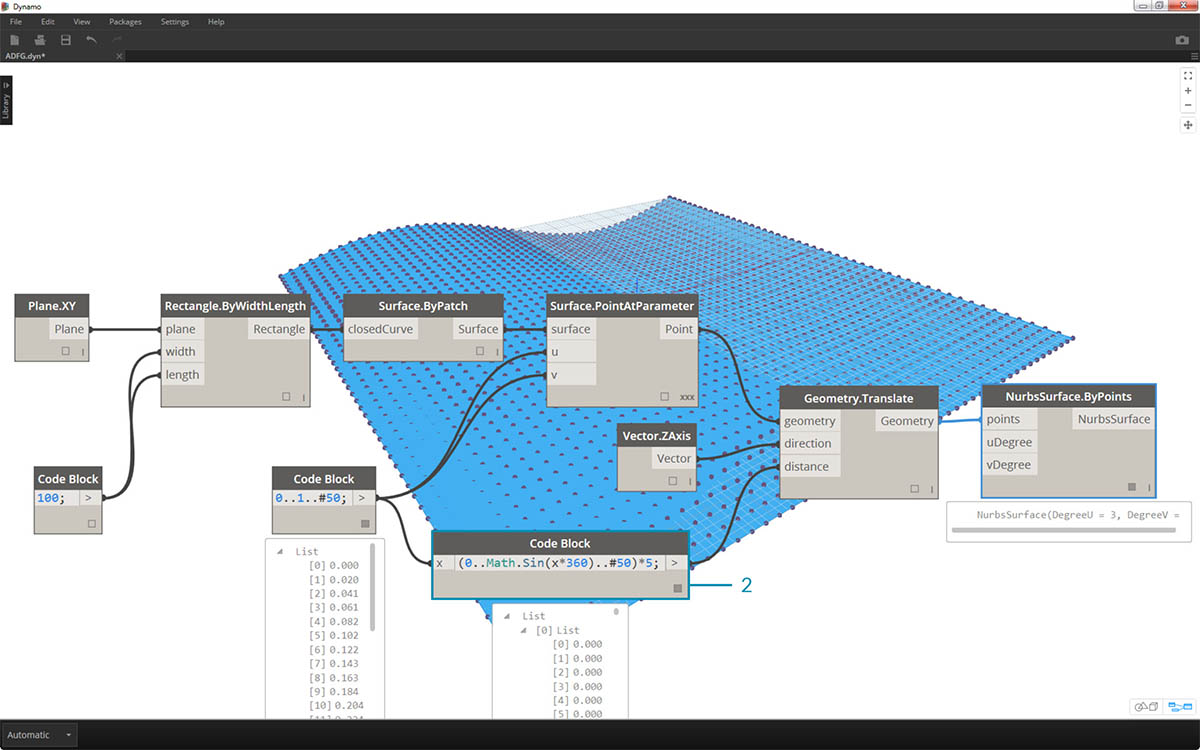
W tym kroku użyjemy pierwszej funkcji do przesunięcia siatki punktów w górę na osi Z. Ta siatka będzie sterować generowaną powierzchnią na podstawie funkcji źródłowej.
- Dodaj węzły wizualne do obszaru rysunku, jak pokazano na ilustracji powyżej.
- Zamiast używać węzła formuły, użyjemy bloku kodu z wierszem:
(0..Math.Sin(x*360)..#50)*5;. Krótkie objaśnienie: definiujemy zakres z formułą w jego wnętrzu. Ta formuła jest funkcją sinus. Funkcja sinus przyjmuje w dodatku Dynamo dane wejściowe w stopniach, więc aby uzyskać pełny kształt funkcji sinus, należy przemnożyć wartości x (jest to wejście zakresu od 0 do 1) przez 360. Następnie chcemy uzyskać taką samą liczbę podziałów, ile jest punktów siatki sterującej dla każdego wiersza, dlatego zdefiniujemy pięćdziesiąt podziałów podrzędnych za pomocą instrukcji #50. Na koniec: mnożnik 5 po prostu zwiększa amplitudę przekształcenia, dzięki czemu możemy zobaczyć efekt w podglądzie Dynamo.
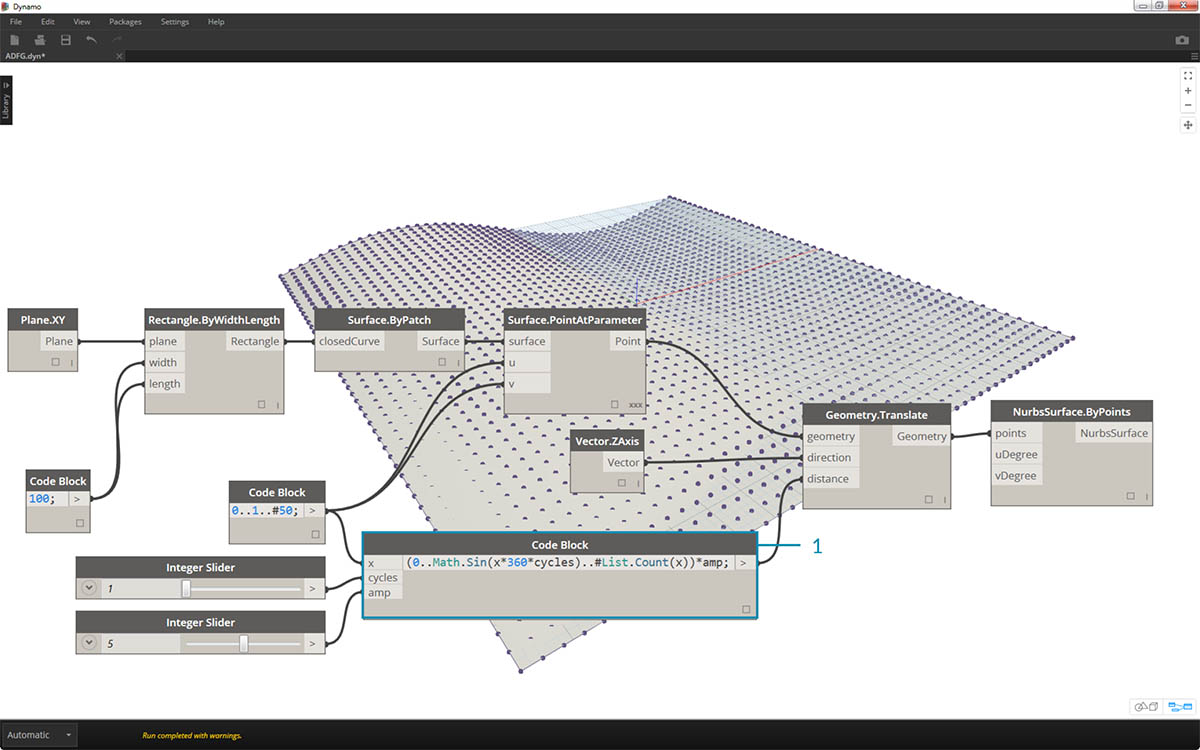
- Mimo że poprzedni blok kodu działał dobrze, nie był całkowicie parametryczny. Chcemy dynamicznie sterować jego parametrami, dlatego zastąpimy wiersz z poprzedniego kroku wierszem
(0..Math.Sin(x*360*cycles)..#List.Count(x))*amp;. Daje to możliwość zdefiniowania tych wartości na podstawie wejść.
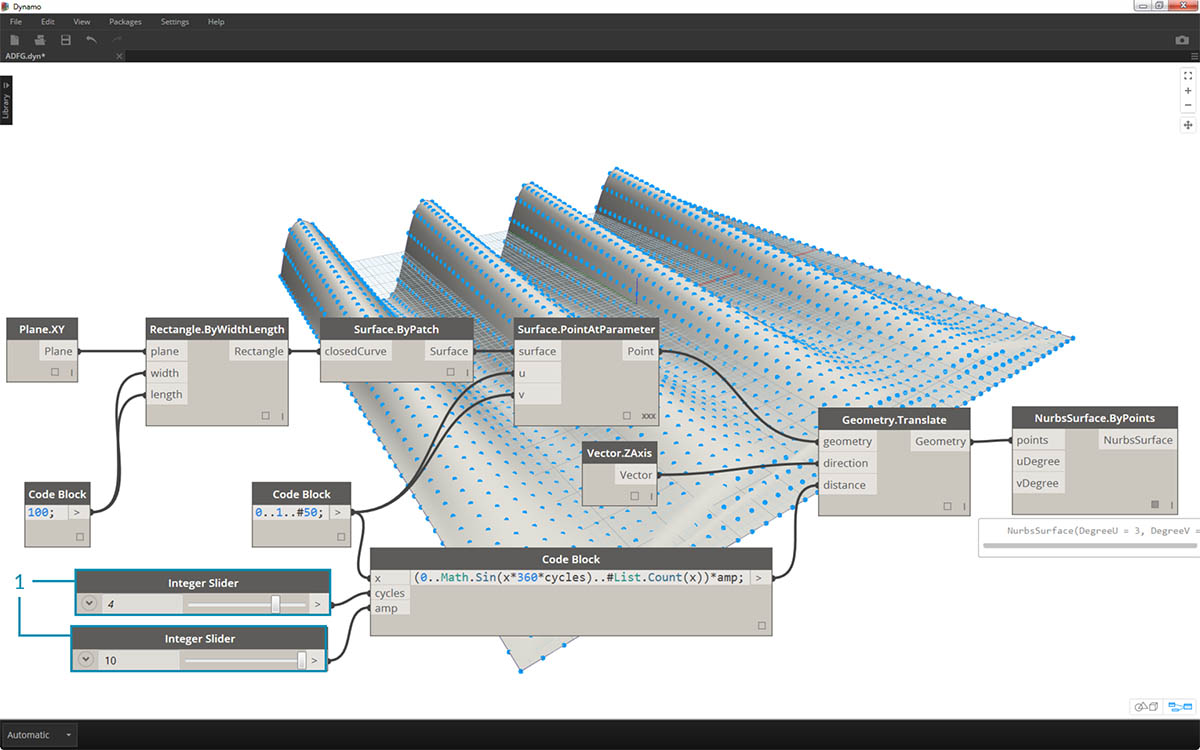
- Zmieniając suwaki (w zakresie od 0 do 10), otrzymujemy interesujące wyniki.
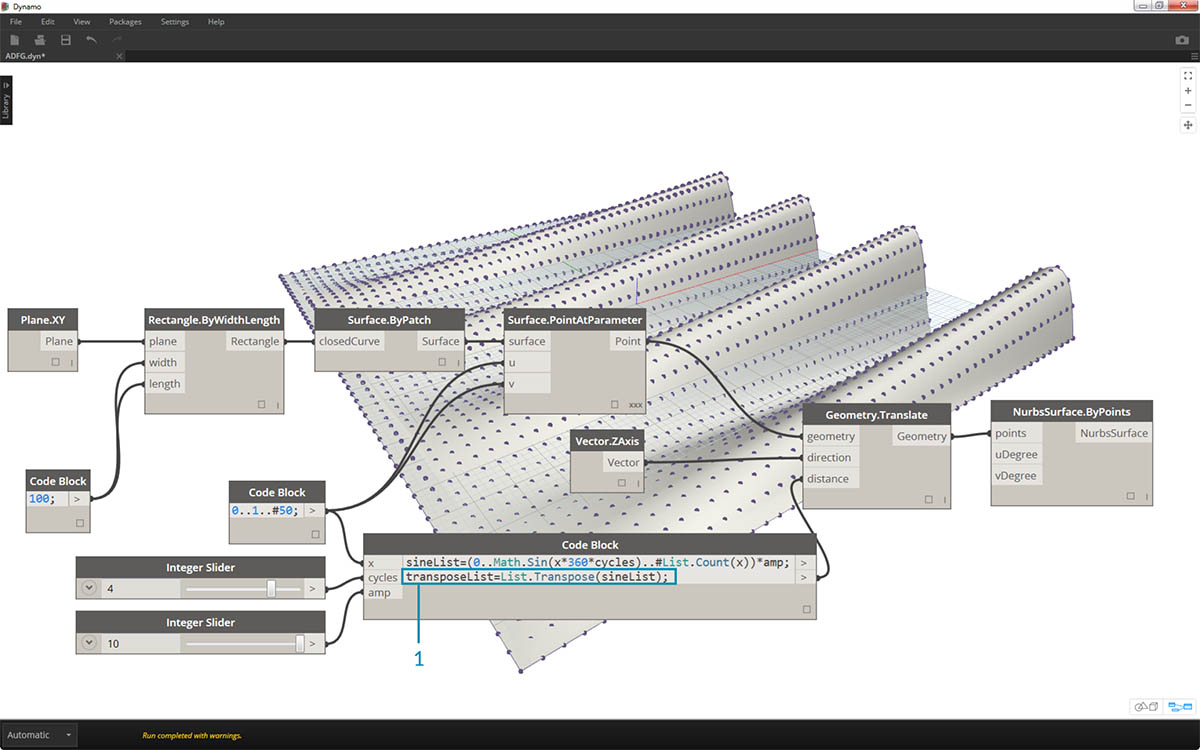
- Transponując zakres liczb, odwrócimy kierunek fali kurtynowej:
transposeList = List.Transpose(sineList);
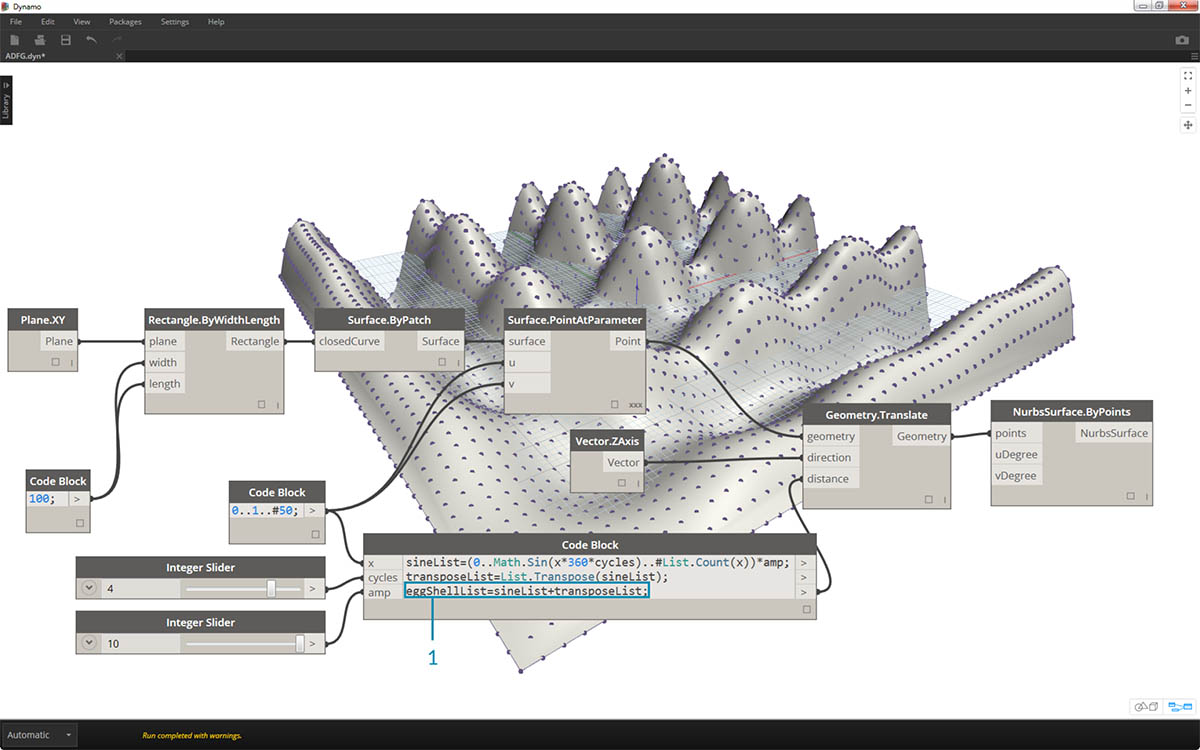
- Po dodaniu wartości sineList i transposeList uzyskujemy zniekształconą „jajowatą” powierzchnię:
eggShellList = sineList+transposeList;
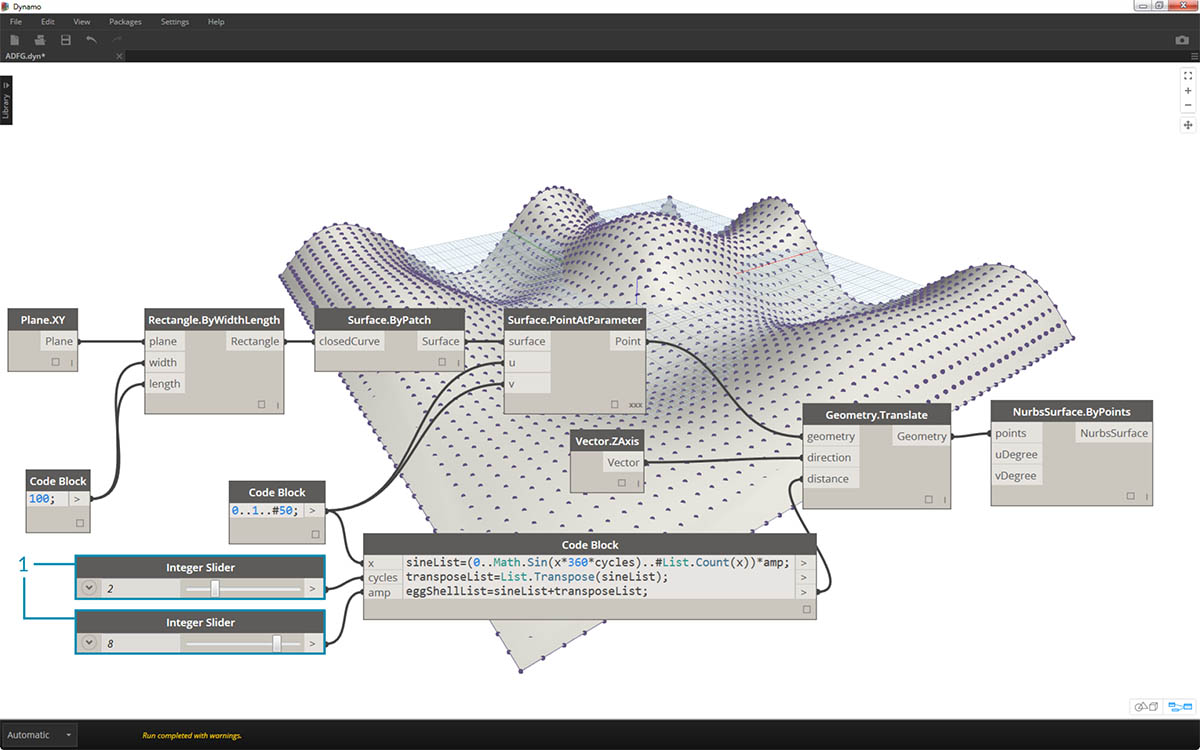
- Ponownie zmieniając suwaki, zmniejszymy zniekształcenia tworzone przez ten algorytm.
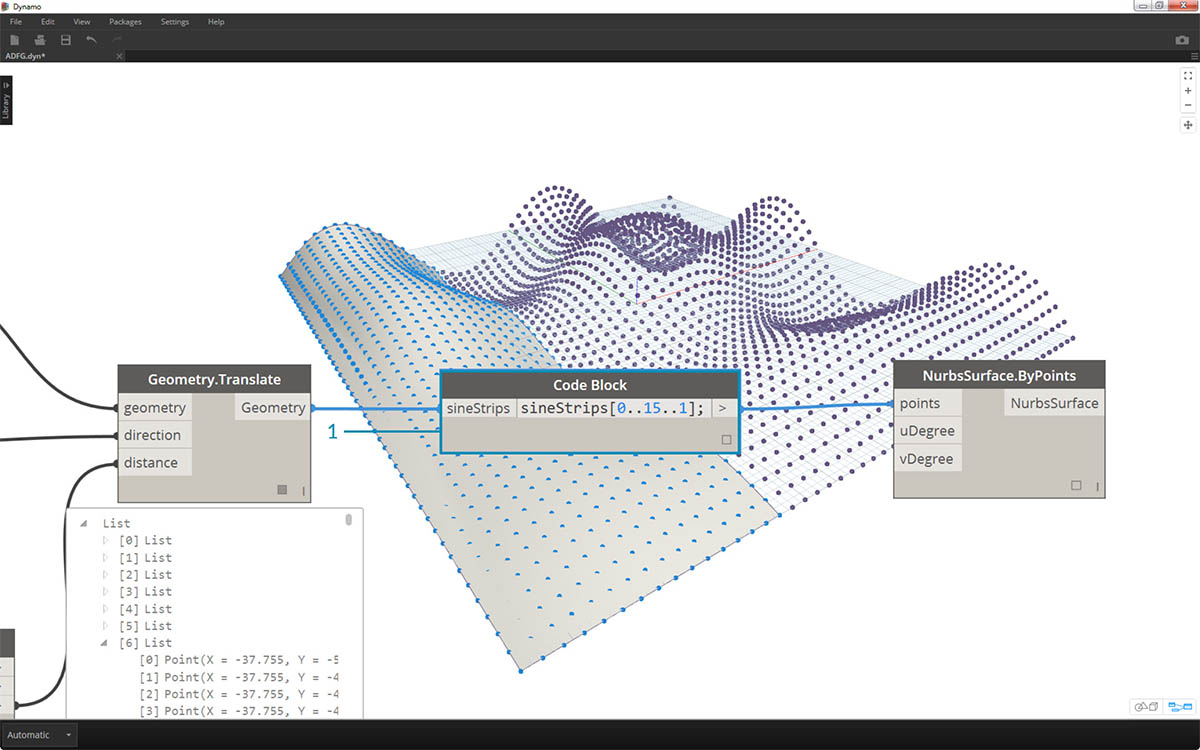
- Na koniec zastosujmy zapytania do wyodrębnionych części danych za pomocą bloku kodu. Aby ponownie wygenerować powierzchnię za pomocą określonego zakresu punktów, dodaj blok kodu powyżej między węzłami Geometry.Translate i NurbsSurface.ByPoints. Będzie on zawierać wiersz tekstu:
sineStrips[0..15..1];. Spowoduje to wybranie pierwszych 16 wierszy punktów (spośród 50). Po ponownym utworzeniu powierzchni widać, że wygenerowaliśmy wyodrębnioną część siatki punktów.
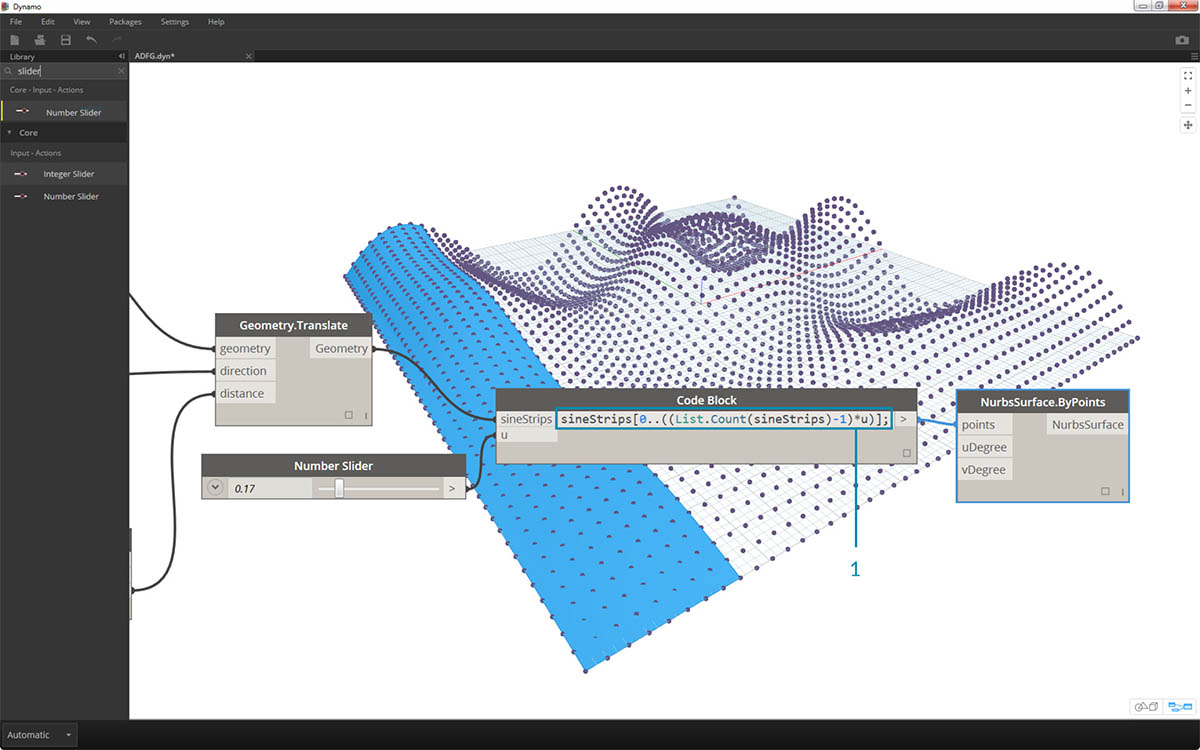
- W ostatnim kroku, aby uczynić ten blok kodu bardziej parametrycznym, będziemy sterować zapytaniem za pomocą suwaka o zakresie od 0 do 1. W tym celu dodamy ten wiersz kodu:
sineStrips[0..((List.Count(sineStrips)-1)*u)];. Może to wydawać się skomplikowane, ale ten wiersz kodu pozwala szybko przeskalować długość listy do mnożnika z zakresu od 0 do 1.
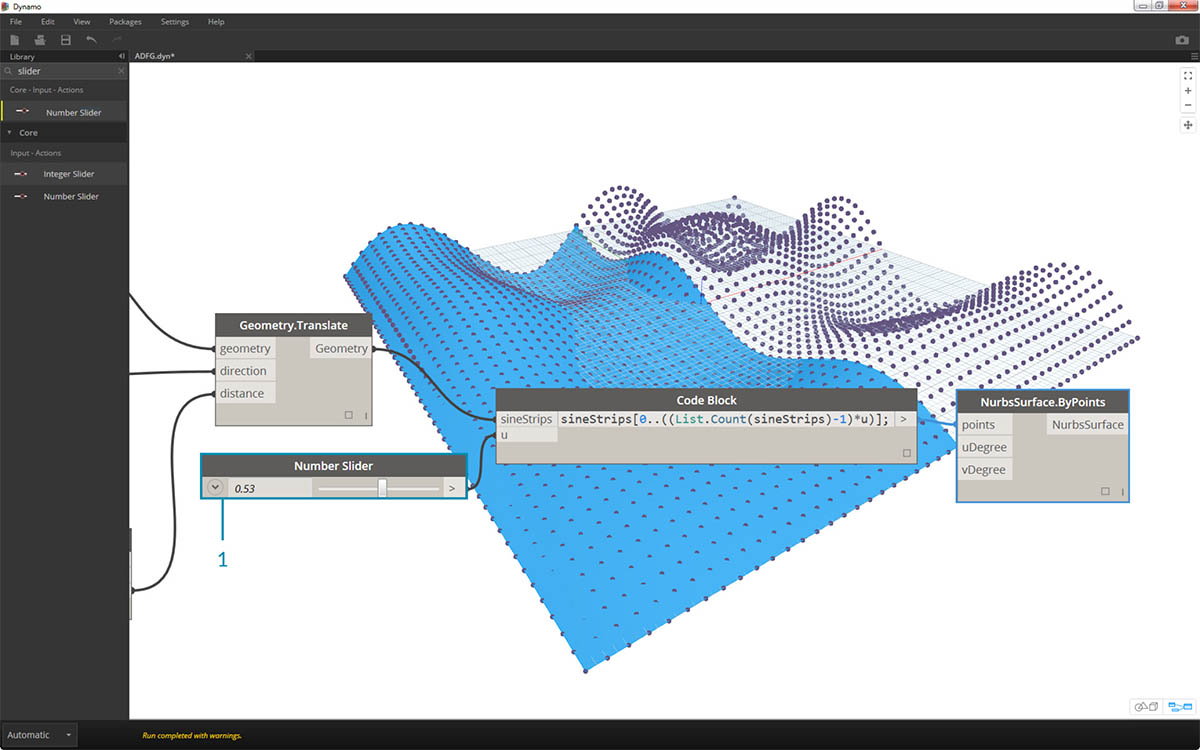
- Wartość 0,53 na suwaku powoduje utworzenie powierzchni tuż za punktem środkowym siatki.
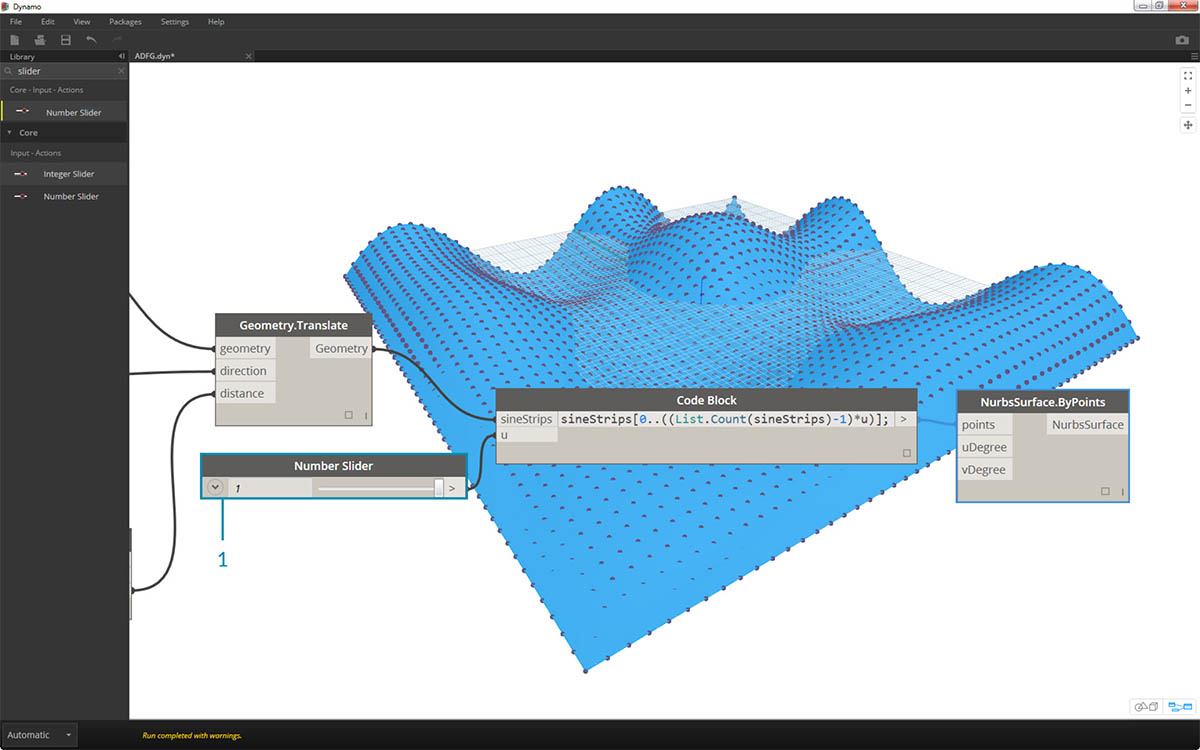
- Zgodnie z oczekiwaniami wartość 1 na suwaku tworzy powierzchnię z pełnej siatki punktów.
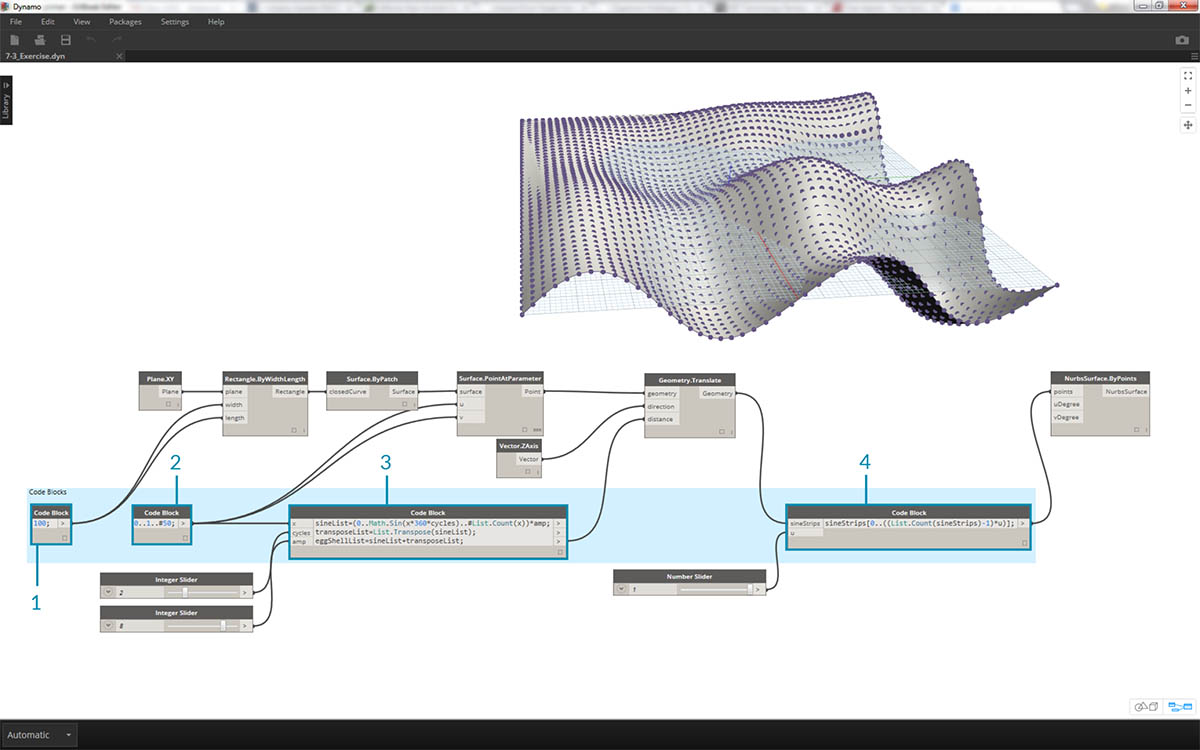
Przyglądając się wynikowemu wykresowi wizualnemu, możemy wyróżnić bloki kodu i przejrzeć ich poszczególne funkcje.
- Pierwszy blok kodu zastępuje węzeł Numer.
- Drugi blok kodu zastępuje węzeł Number Range.
- Trzeci blok kodu zastępuje węzeł Formula (jak również węzły List.Transpose, List.Count i Number Range).
- Czwarty blok kodu stosuje zapytania do listy list, zastępując węzeł List.GetItemAtIndex.