Bryły

Jeśli chcemy tworzyć bardziej złożone modele, których nie można utworzyć z pojedynczej powierzchni, lub jeśli chcemy zdefiniować dokładną objętość, musimy teraz omówić bryły (i polipowierzchnie). Nawet prosty sześcian jest wystarczająco złożony, aby wymagać sześciu powierzchni — po jednej na ścianę. Bryły zapewniają dostęp do dwóch kluczowych pojęć, które nie istnieją w przypadku powierzchni — bardziej szczegółowego opisu topologicznego (powierzchni, krawędzi, wierzchołków) i operacji logicznych.

Co to jest bryła?

Bryły składają się z jednej lub większej liczby powierzchni, które obejmują objętość w ramach zamkniętej obwiedni definiującej kierunek „do wewnątrz” lub „na zewnątrz”. Niezależnie od tego, ile jest tych powierzchni, muszą one tworzyć „szczelną” objętość, aby można było je uważać za bryłę. Bryły można tworzyć przez połączenie powierzchni lub polipowierzchni albo za pomocą operacji, takich jak wyciągnięcie złożone, przeciągnięcie i obrót. Obiekty elementarne takie jak sfera, sześcian, stożek i walec są również bryłami. Sześcian z usuniętą co najmniej jedną powierzchnią to polipowierzchnia, która ma podobne właściwości, ale nie jest bryłą.

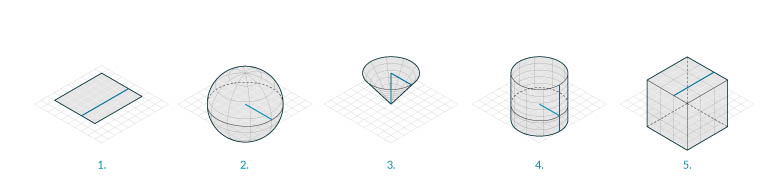
1. Płaszczyzna składa się z pojedynczej powierzchni i nie jest bryłą.
2. Sfera składa się z pojedynczej powierzchni, ale jest bryłą.
3. Stożek składa się z dwóch połączonych ze sobą powierzchni tworzących bryłę.
4. Walec składa się z trzech połączonych ze sobą powierzchni tworzących bryłę.
5. Sześcian składa się z sześciu połączonych ze sobą powierzchni tworzących bryłę.

Topologia

Bryły składają się z trzech typów elementów: wierzchołków, krawędzi i ścian. Ściany to powierzchnie tworzące bryłę. Krawędziami są krzywe definiujące połączenie pomiędzy przyległymi ścianami, a wierzchołki to punkty początkowe i końcowe tych krzywych. Te elementy mogą być przywoływane za pomocą węzłów topologii.

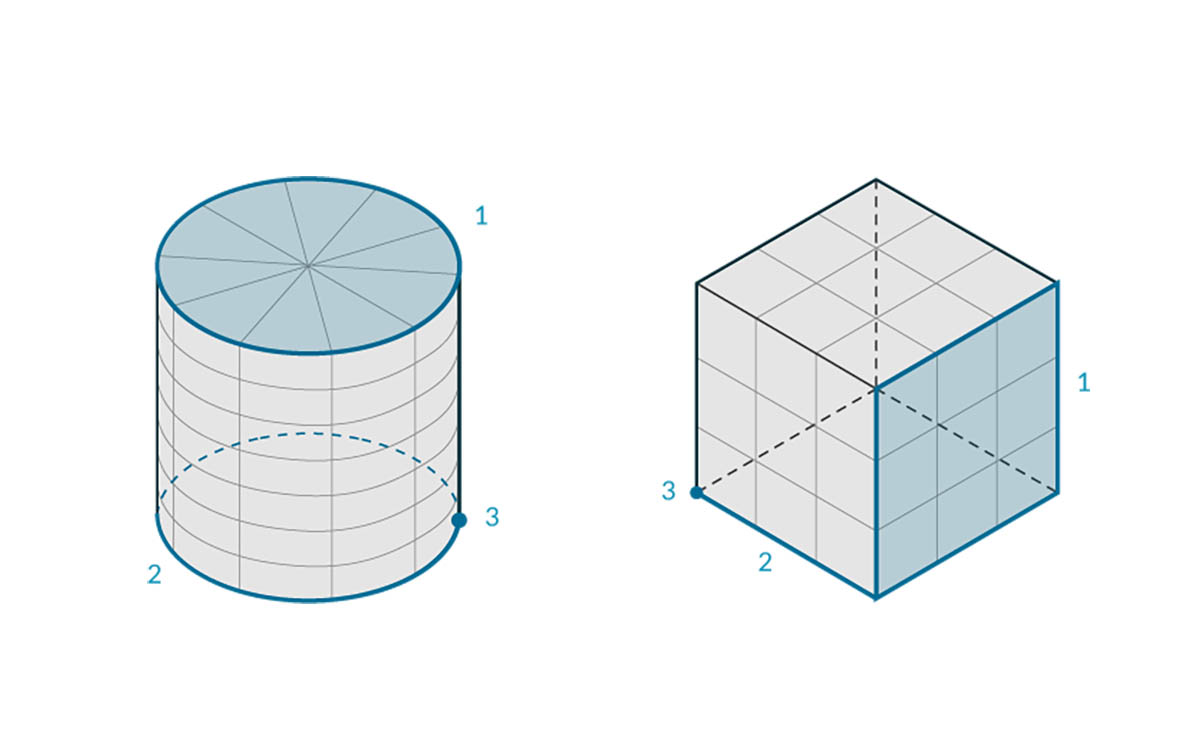
1. Powierzchnie
2. Krawędzie
3. Wierzchołki

Operacje

Bryły można modyfikować przez zaokrąglenie lub fazowanie ich krawędzi w celu wyeliminowania ostrych narożników i kątów. Operacja fazowania tworzy powierzchnię prostokreślną między dwiema ścianami, natomiast zaokrąglenie łączy ściany, aby zachować styczność.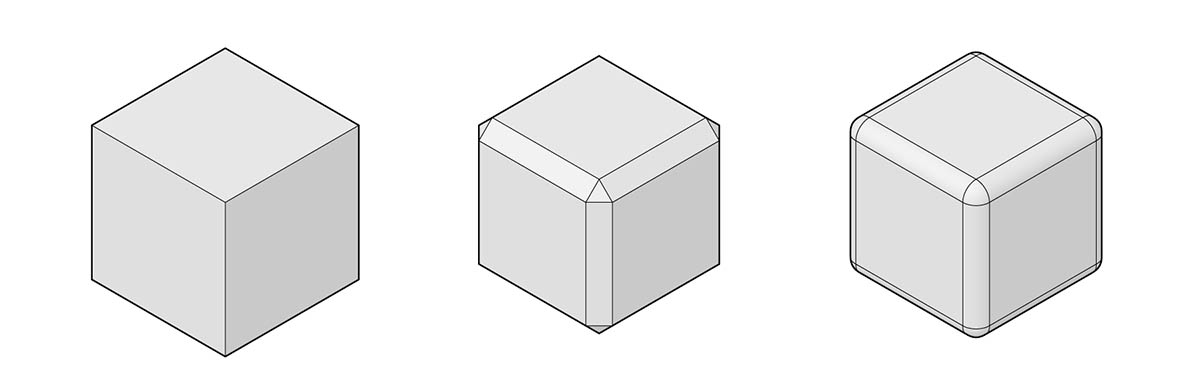

1. Przygotówka
2. Sześcian z fazowaniem
3. Sześcian z zaokrągleniami

Operacje logiczne

Operacje logiczne na bryłach są metodami łączenia dwóch lub większej liczby brył. Pojedyncza operacja logiczna oznacza właściwie wykonanie czterech operacji:

1. Przecięcie dwóch lub większej liczby obiektów.
2. Podzielenie ich w punktach przecięcia.
3. Usunięcie niepotrzebnych części geometrii.
4. Połączenie wszystkiego z powrotem.

Dzięki temu operacje logiczne na bryłach są zaawansowanym i oszczędzającym czas procesem. Istnieją trzy operacje logiczne na bryłach rozróżniające, które części geometrii zostają zachowane.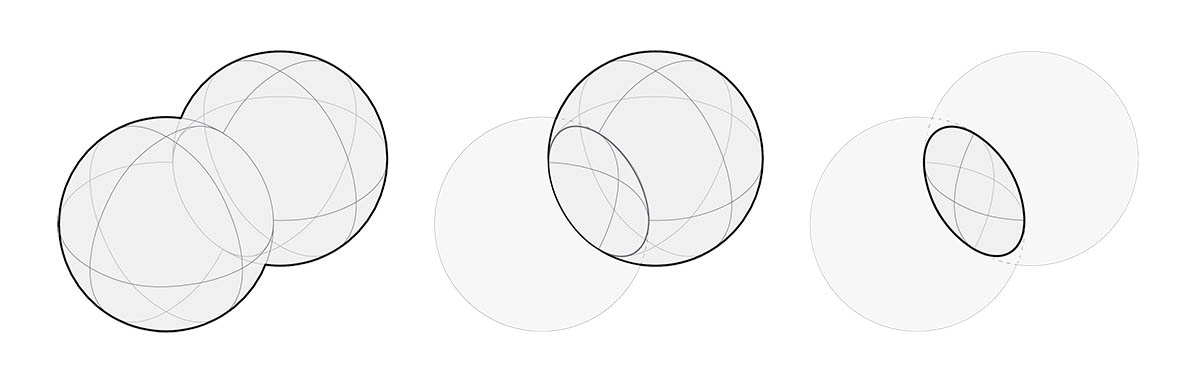

1. Union (suma): usuń nakładające się części brył i połącz je w jedną bryłę.
2. Difference (różnica): odejmij jedną bryłę od drugiej. Bryła odejmowana jest określana jako narzędzie. Warto zauważyć, że można zamienić bryłę wskazaną jako narzędzie, aby zachować odwrotną objętość.
3. Intersection (przecięcie): zachowaj tylko przecinającą się objętość dwóch brył.

Oprócz tych trzech operacji dodatek Dynamo udostępnia też węzły Solid.DifferenceAll i Solid.UnionAll, które umożliwiają wykonywanie operacji różnicy i sumy dla wielu brył.

1. UnionAll: operacja sumy ze sferą i stożkami skierowanymi na zewnątrz
2. DifferenceAll: operacja różnicy ze sferą i stożkami skierowanymi do wewnątrz

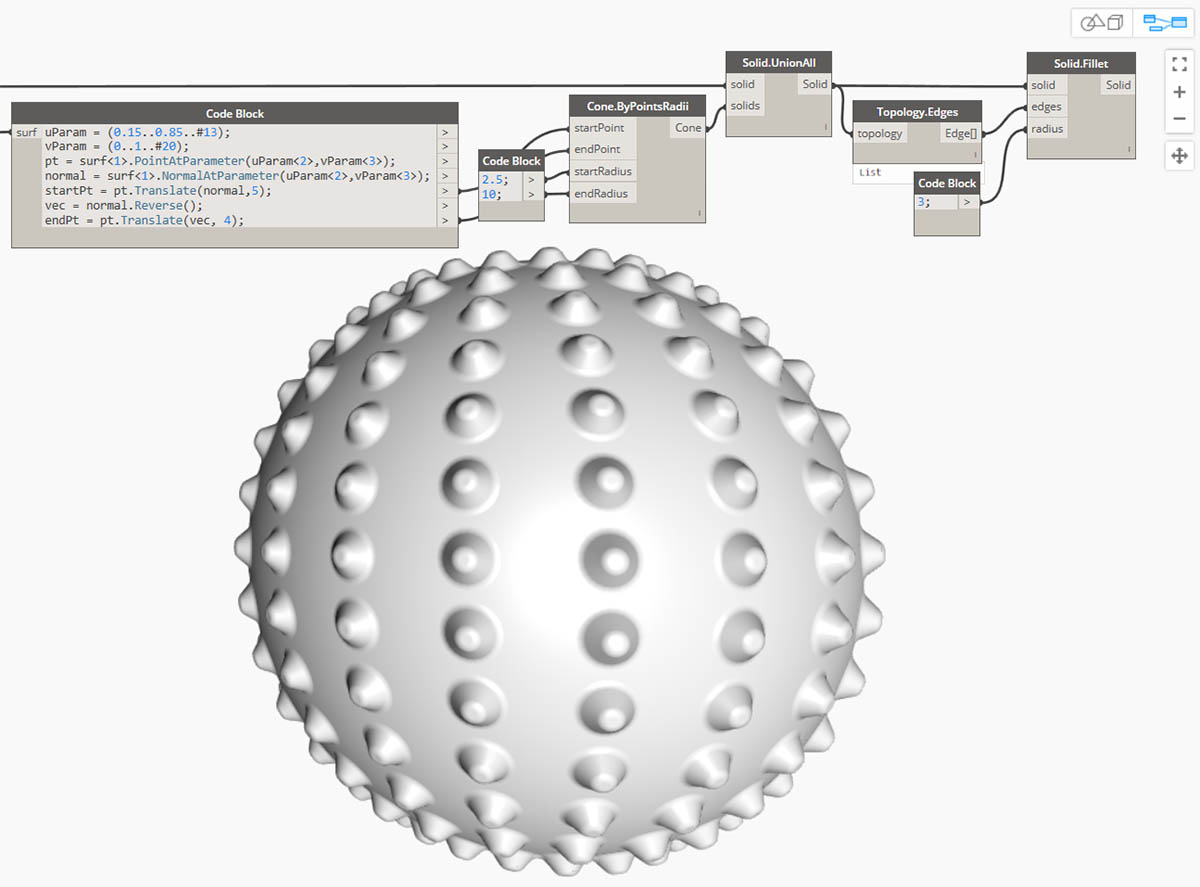
Użyjmy kilku operacji logicznych, by utworzyć kolczastą kulę.

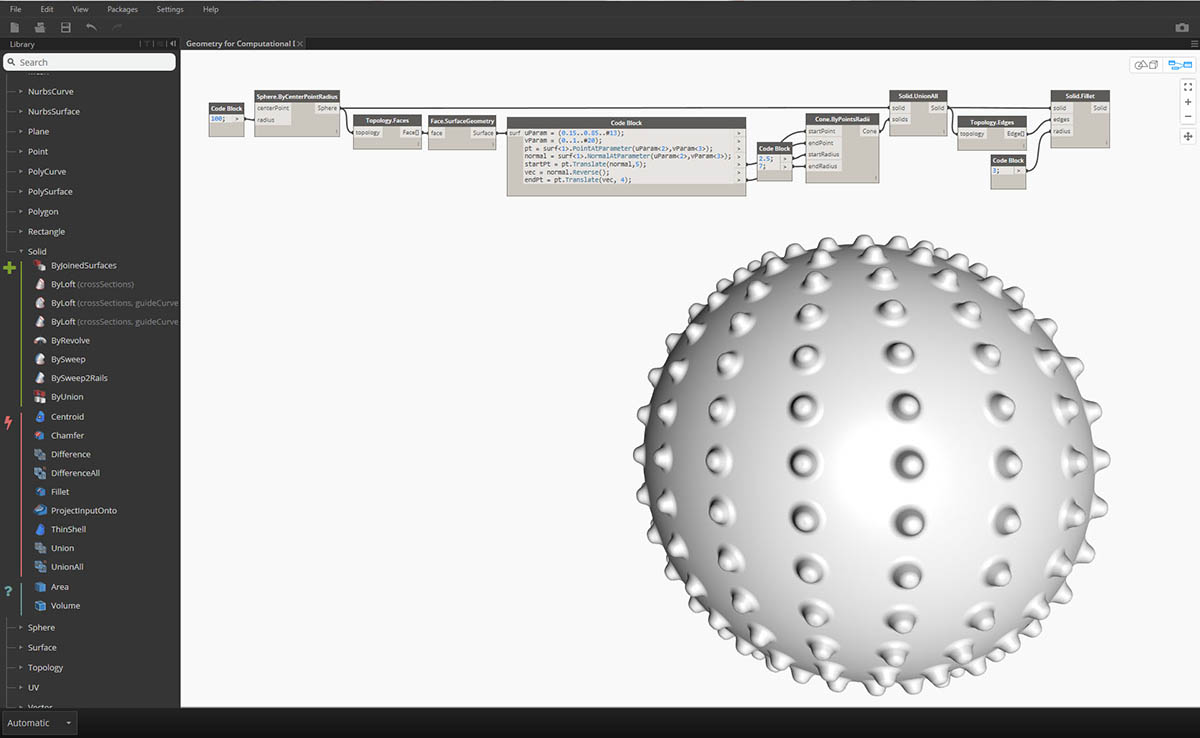
1. Sphere.ByCenterPointRadius: utwórz bryłę bazową.
2. Topology.Faces, Face.SurfaceGeometry: wykonaj zapytanie dotyczące powierzchni bryły i przekształć w geometrię powierzchni — w tym przypadku sfera ma tylko jedną powierzchnię.
3. Cone.ByPointsRadii: utwórz stożki przy użyciu punktów na powierzchni.
4. Solid.UnionAll: zsumuj stożki i sferę.
5. Topology.Edges: wykonaj zapytanie dotyczące krawędzi nowej bryły.
6. Solid.Fillet: dodaj do krawędzi kolczastej kuli zaokrąglenia. Pobierz pliki przykładowe do tego obrazu (kliknij prawym przyciskiem myszy i wybierz polecenie Zapisz element docelowy jako). Pełna lista plików przykładowych znajduje się w załączniku. Geometry for Computational Design - Solids.dyn

Blokowanie

Operacje logiczne są złożone i ich obliczanie może być powolne. Funkcja blokowania pozwala wstrzymać wykonywanie wybranych węzłów i zależnych od nich węzłów na dalszym etapie przepływu.

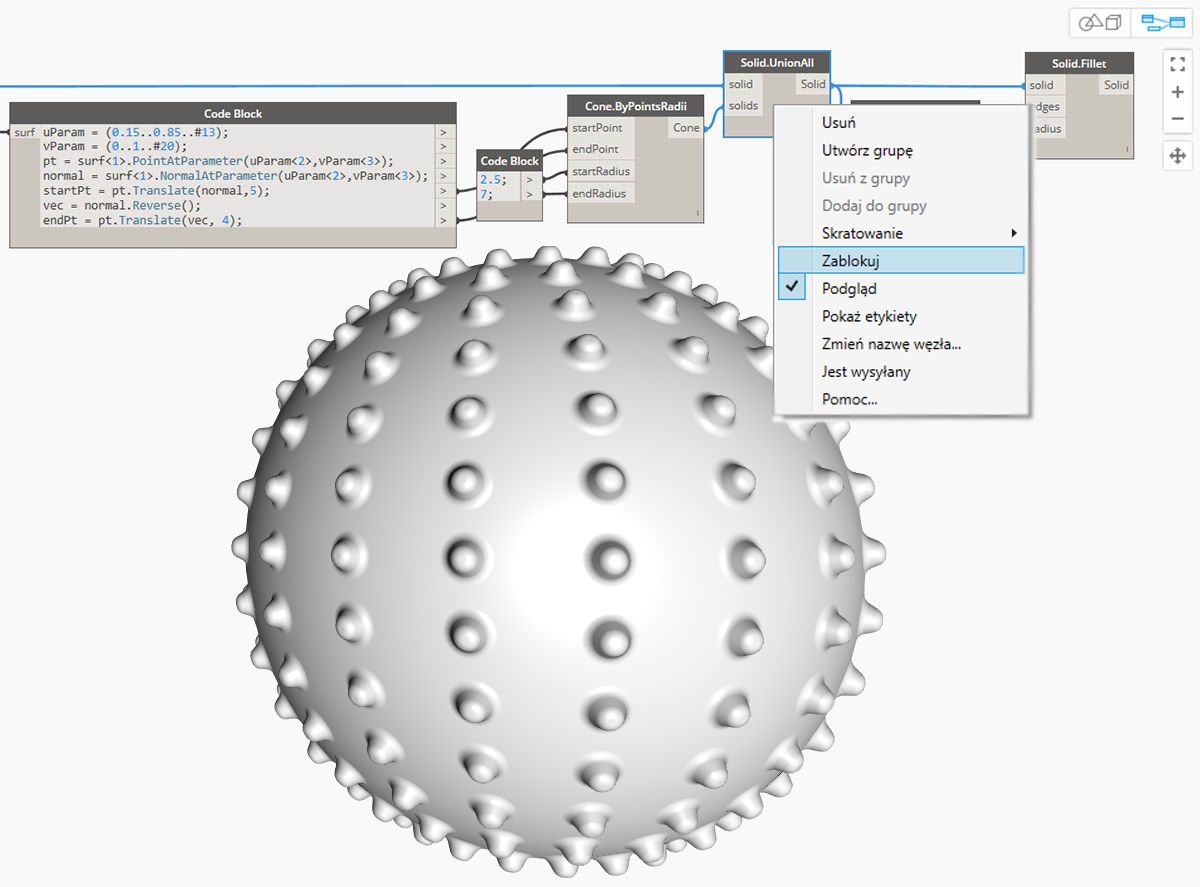
Użyj menu kontekstowego wyświetlanego po kliknięciu prawym przyciskiem myszy, aby zablokować operację sumowania brył

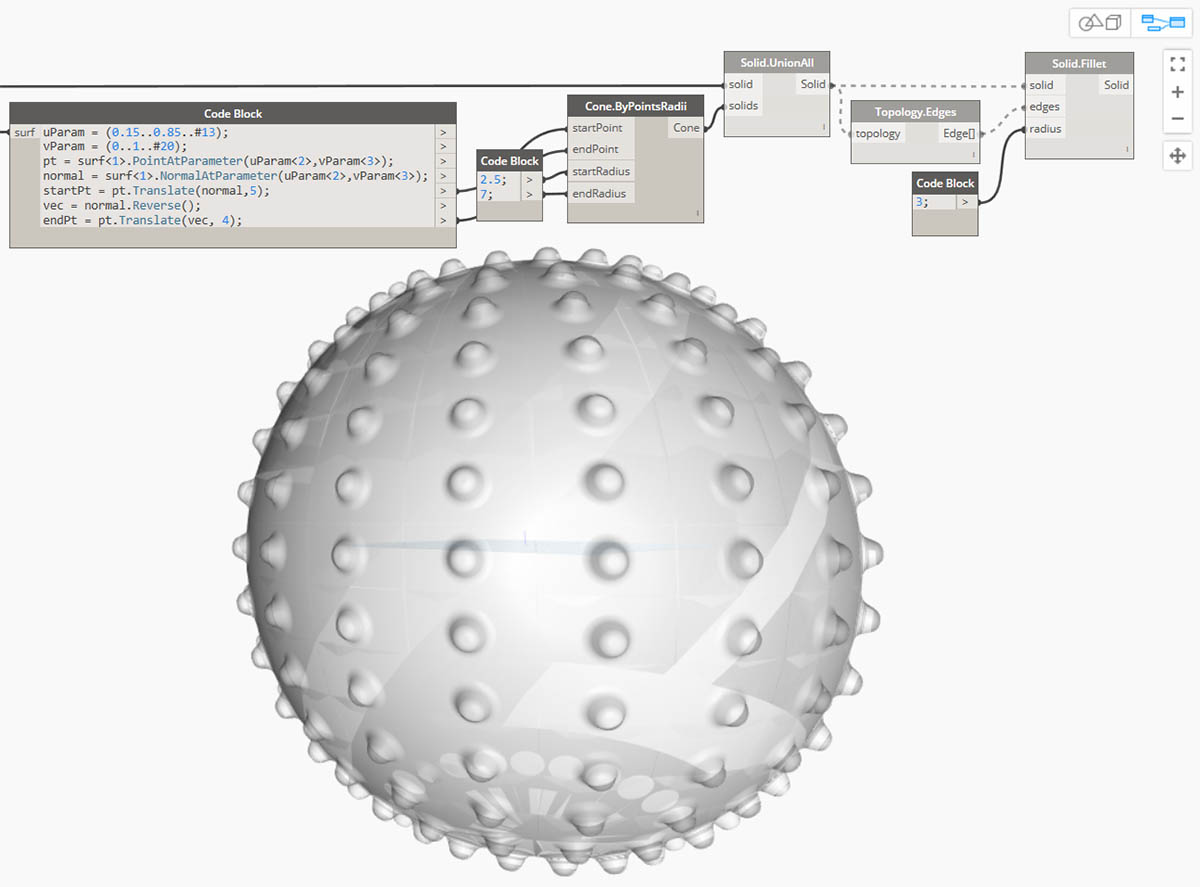
Wybrany węzeł i wszystkie węzły na dalszym etapie przepływu będą wyświetlane w podglądzie z jasnoszarym cieniowaniem, a zależne przewody będą wyświetlane jako linie kreskowane. Także zależny podgląd geometrii będzie cieniowany. Teraz można zmienić wartości na wcześniejszym etapie przepływu bez obliczania sumy logicznej.

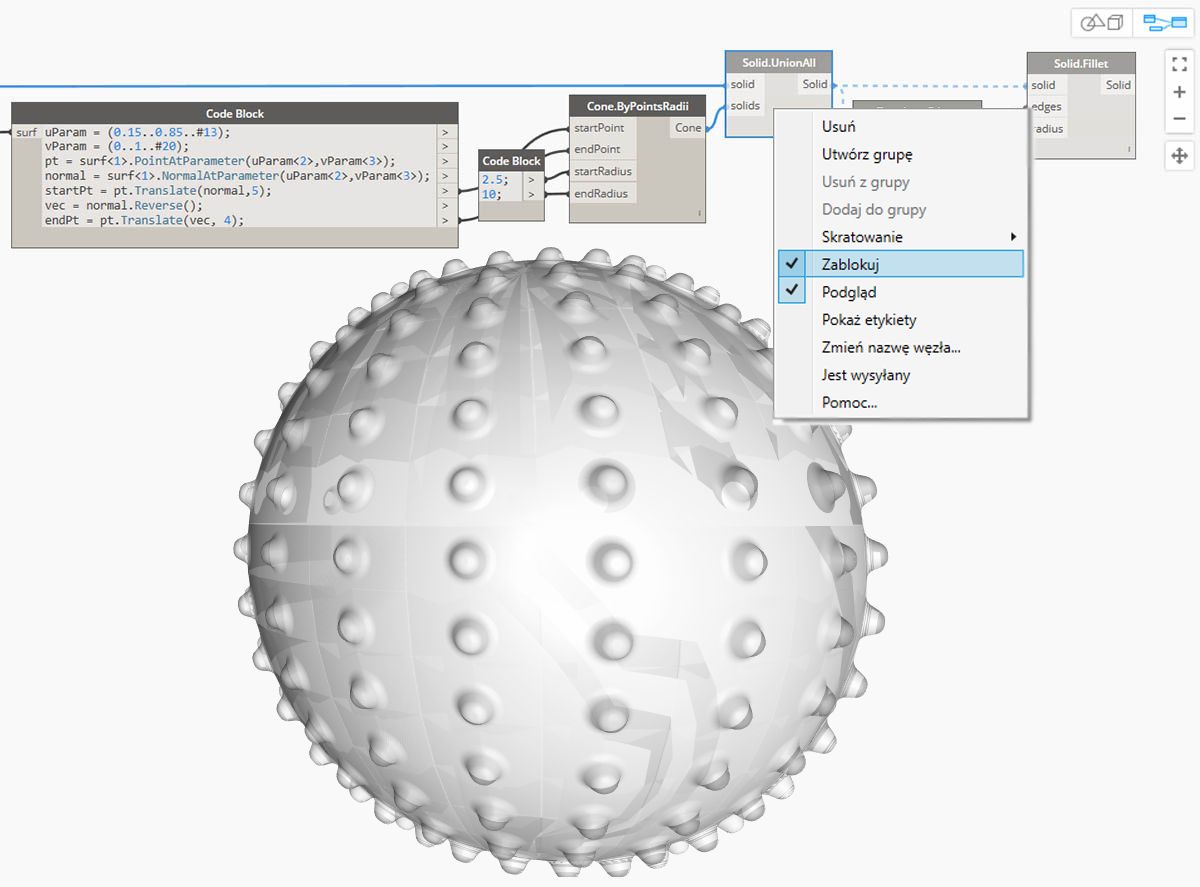
Aby odblokować węzły, kliknij prawym przyciskiem myszy i wyczyść pole wyboru Zablokuj.

Wszystkie zależne węzły i skojarzone podglądy geometrii zostaną zaktualizowane i wrócą do standardowego trybu podglądu.