Punkty

Jeśli geometria jest językiem modelu, punkty są alfabetem. Punkty są podstawą tworzenia całej geometrii — do utworzenia krzywej potrzebne są co najmniej dwa punkty, do utworzenia wieloboku lub powierzchni siatki potrzebne są co najmniej trzy punkty itd. Zdefiniowanie położenia, kolejności i relacji między punktami (np. funkcji sinus) umożliwia zdefiniowanie geometrii wyższego rzędu, takich jak elementy rozpoznawane przez użytkownika jako okręgi lub krzywe.

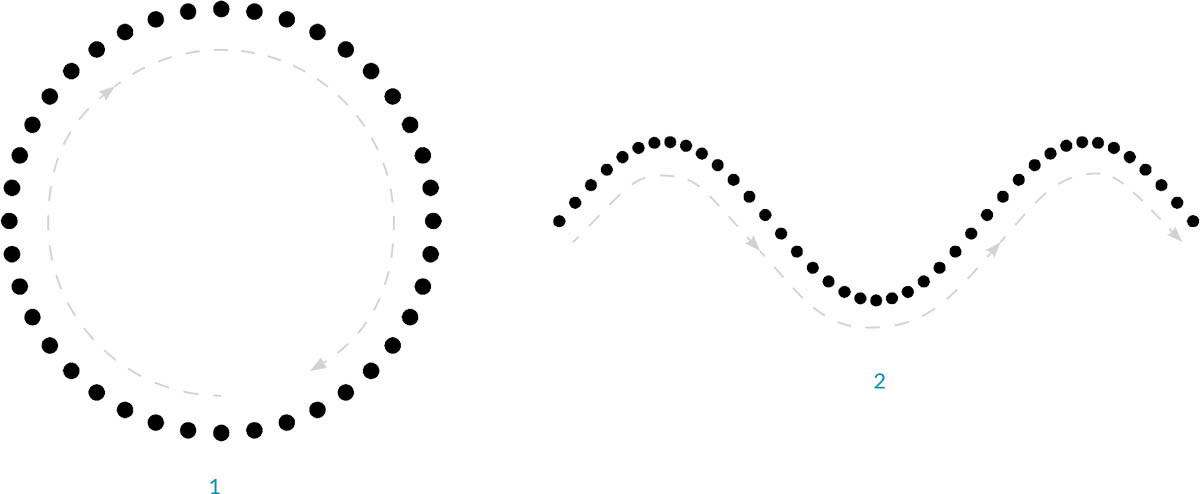
1. Okrąg na podstawie funkcji x=r*cos(t) i y=r*sin(t)
2. Krzywa sinusoidalna na podstawie funkcji x=(t) i y=r*sin(t)

Co to jest punkt?

Punkt jest zdefiniowany przez tylko jedną wartość lub tylko kilka wartości nazywanych współrzędnymi. Liczba wartości współrzędnych potrzebnych do zdefiniowania punktu zależy od układu współrzędnych lub kontekstu, w którym się on znajduje. Najczęściej używany typ punktu w dodatku Dynamo istnieje w trójwymiarowym globalnym układzie współrzędnych i ma trzy współrzędne [X,Y,Z].

Punkt jako współrzędne

Punkty mogą również występować w dwuwymiarowym układzie współrzędnych. Konwencja wskazuje różne notacje literowe w zależności od tego, z którym typem przestrzeni pracujemy — możemy używać [X,Y] na płaszczyźnie lub [U,V] na powierzchni.

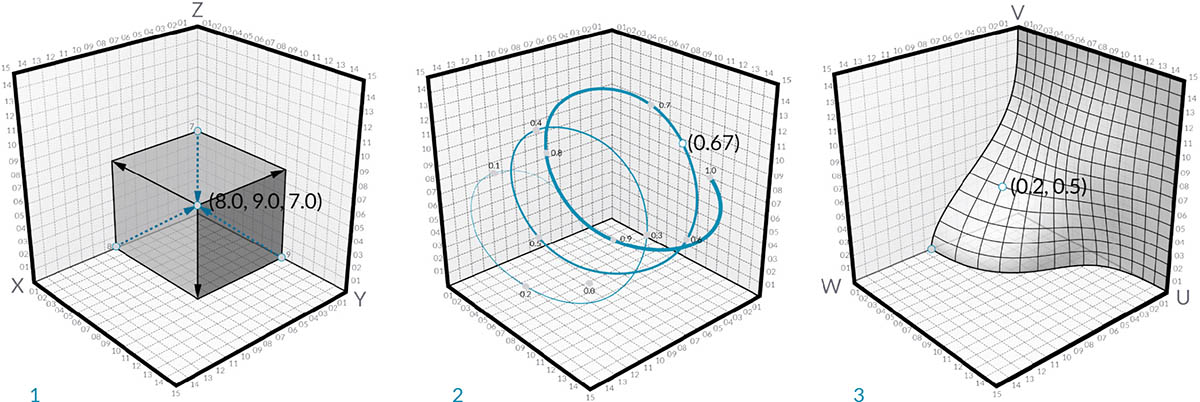
1. Punkt w euklidesowym układzie współrzędnych: [X,Y,Z]
2. Punkt w układzie współrzędnych z parametrem krzywej: [t]
3. Punkt w układzie współrzędnych z parametrami powierzchni: [U,V]

Mimo że wydaje się to sprzeczne z intuicją, parametry dla krzywych i powierzchni są ciągłe i rozciągają się poza krawędź danej geometrii. Ponieważ kształty definiujące przestrzeń parametryczną znajdują się w trójwymiarowym globalnym układzie współrzędnych, zawsze można przekształcić współrzędną parametryczną we współrzędną „globalną”. Na przykład punkt [0,2, 0,5] na powierzchni jest taki sam jak punkt [1,8, 2,0, 4,1] we współrzędnych globalnych.

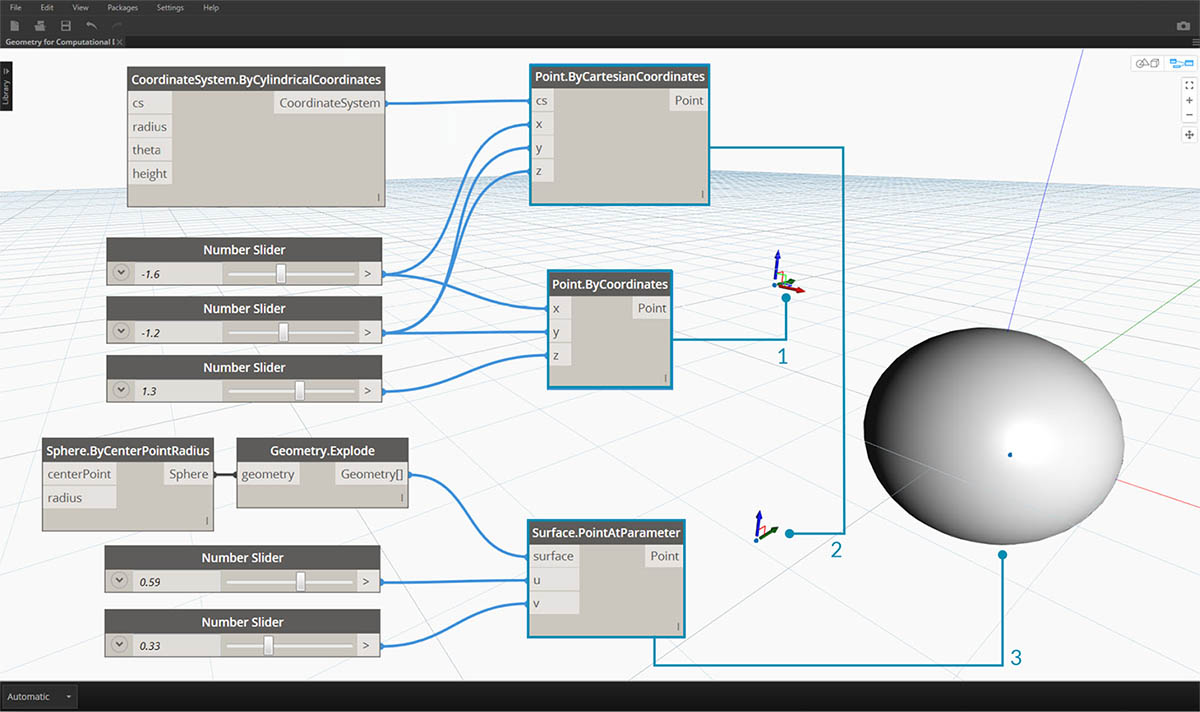
1. Punkt w zakładanych współrzędnych globalnych XYZ
2. Punkt względem danego układu współrzędnych (walcowego)
3. Punkt jako współrzędne UV na powierzchni Pobierz plik przykładowy do tego obrazu (kliknij prawym przyciskiem myszy i wybierz opcję Zapisz element docelowy jako): Geometry for Computational Design - Points.dyn. Pełna lista plików przykładowych znajduje się w załączniku.