Listy n-wymiarowe

Idąc dalej, możemy dodać jeszcze więcej poziomów do hierarchii. Struktura danych może znacznie wykraczać poza dwuwymiarową listę list. Ponieważ same listy również są elementami w dodatku Dynamo, możemy tworzyć dane z dowolnie dużą liczbą wymiarów.

Można to porównać do rosyjskich matrioszek. Każdą listę można traktować jako jeden pojemnik zawierający wiele elementów. Każda lista ma określone właściwości i sama w sobie jest traktowana jako obiekt.

Zestaw matrioszek (autor zdjęcia: Zeta) to dobra analogia dla list n-wymiarowych. Każda warstwa oznacza listę, a każda lista zawiera elementy. W dodatku Dynamo każdy pojemnik może zawierać wiele pojemników (elementów listy).

Listy n-wymiarowe trudno przedstawić wizualnie, ale w tym rozdziale przygotowaliśmy kilka ćwiczeń dotyczących pracy z listami wykraczającymi poza dwa wymiary.

Odwzorowywanie i kombinacje

Odwzorowywanie to zdecydowanie najbardziej złożona część zarządzania danymi w programie Dynamo, szczególnie istotna podczas pracy ze złożonymi hierarchiami list. W poniższych ćwiczeniach pokazano, kiedy używać odwzorowywania i kombinacji podczas pracy z wielowymiarowymi danymi.

Wstępne informacje o węzłach List.Map i List.Combine można znaleźć w poprzedniej sekcji. W ostatnim ćwiczeniu użyjemy tych węzłów w złożonej strukturze danych.

Ćwiczenie — listy dwuwymiarowe — podstawowe

Pobierz pliki przykładowe do tego ćwiczenia (kliknij prawym przyciskiem myszy i wybierz polecenie Zapisz element docelowy jako). Pełna lista plików przykładowych znajduje się w Załączniku. 1.n-Dimensional-Lists.dyn 2.n-Dimensional-Lists.sat

To pierwsze z serii trzech ćwiczeń, które skupia się na artykulacji zaimportowanej geometrii. W każdej części tej serii ćwiczeń zwiększy się złożoność struktury danych.

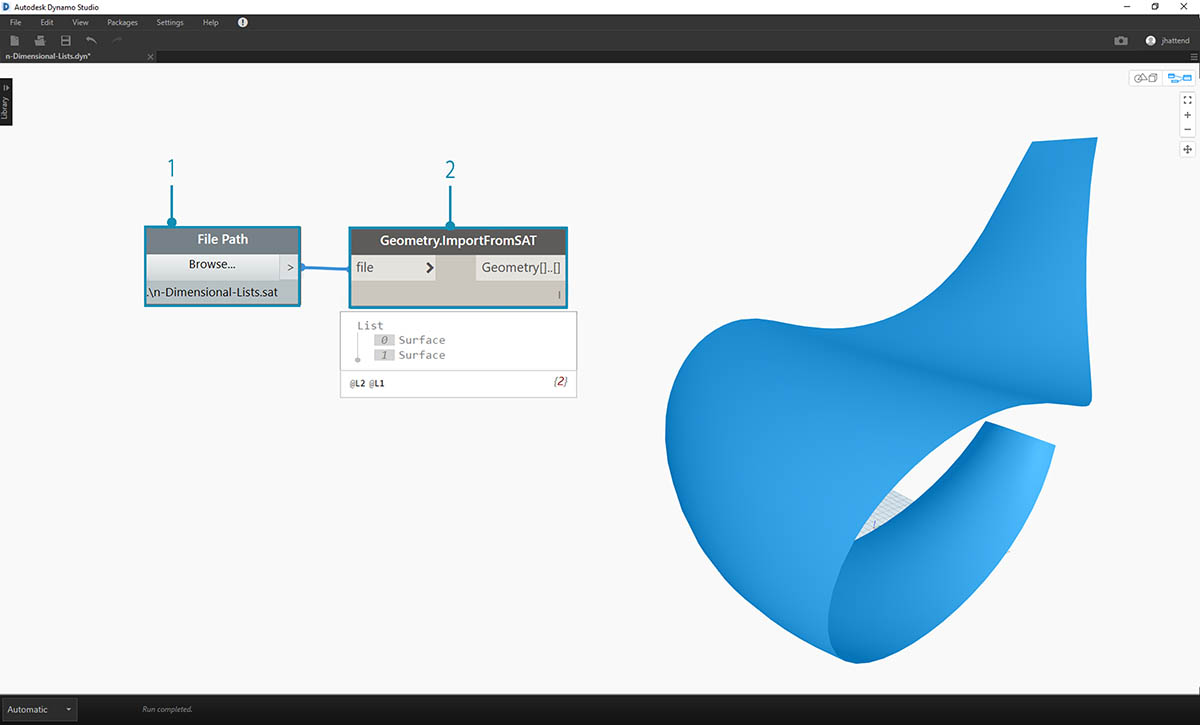
1. Zacznijmy od pliku .sat w folderze plików ćwiczeniowych. Można przechwycić ten plik za pomocą węzła File Path.
2. Za pomocą węzła Geometry.ImportFromSAT geometria jest importowana do podglądu dodatku Dynamo jako dwie powierzchnie.

Aby uprościć to ćwiczenie, będziemy pracować z jedną z tych powierzchni.

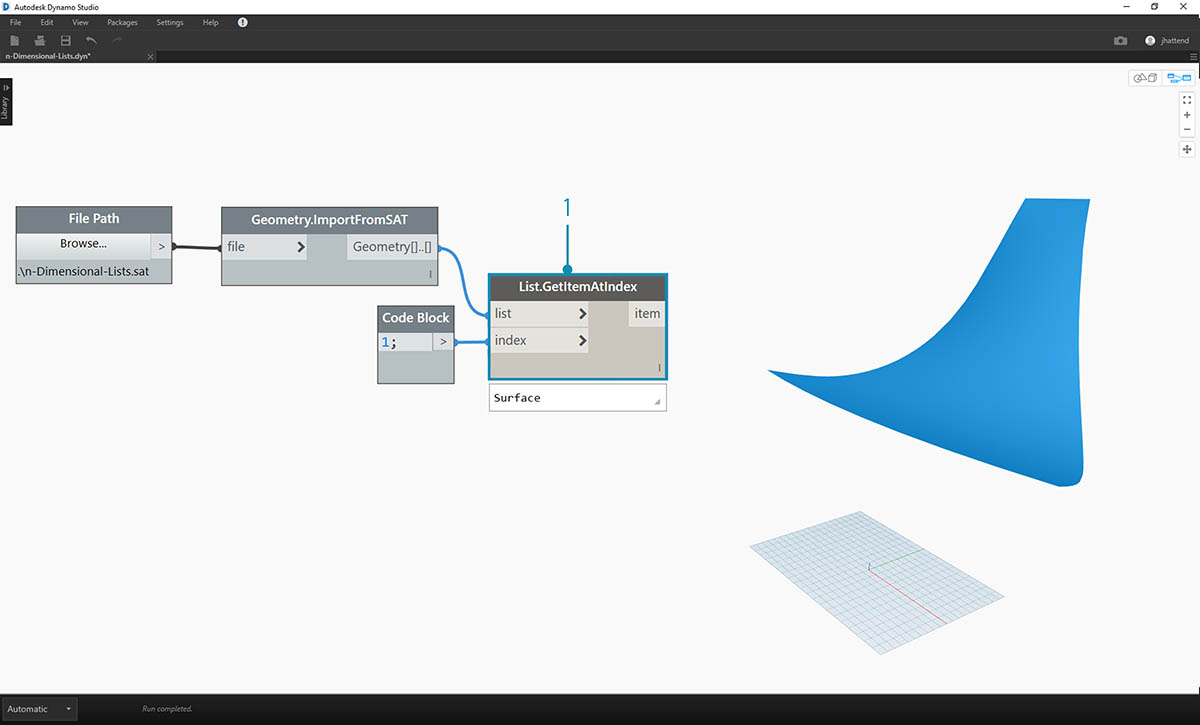
1. Wybierzmy indeks 1 , aby przechwycić górną powierzchnię. Służy do tego węzeł List.GetItemAtIndex.

Kolejnym etapem jest podzielenie powierzchni na siatkę punktów.

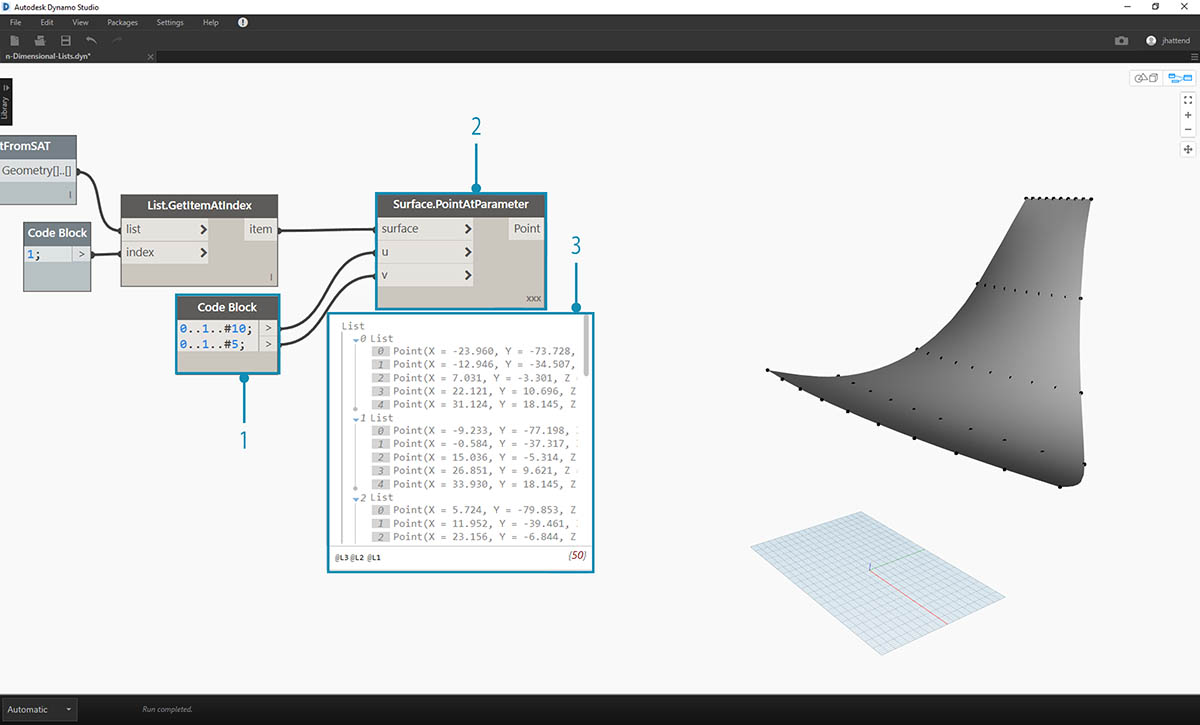
1. Za pomocą węzła Code Block wstaw następujące dwa wiersze kodu:

   0..1..#10;
   0..1..#5;
   

1. W węźle Surface.PointAtParameter połącz te dwie wartości z bloku kodu z elementami u i v. Zmień opcję skratowania tego węzła na „Iloczyn wektorowy”.
2. Wynik pokazuje strukturę danych, która jest również widoczna w podglądzie dodatku Dynamo.

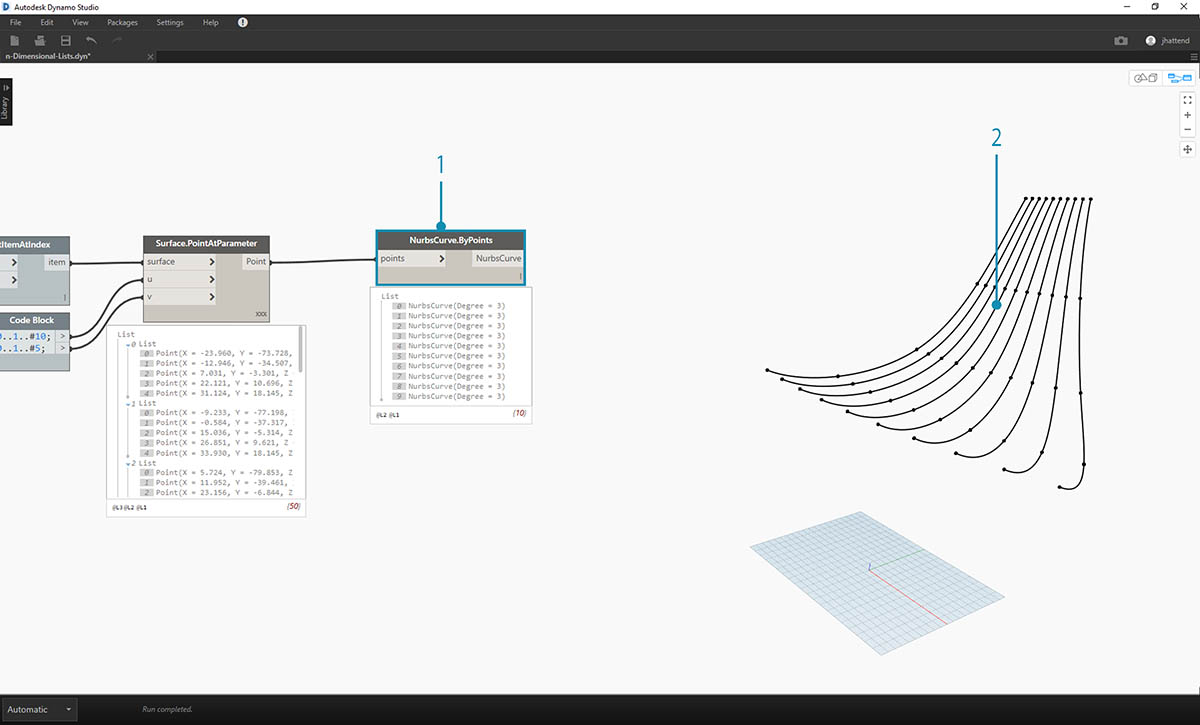
1. Aby zobaczyć, jak zorganizowana jest struktura danych, połączmy węzeł NurbsCurve.ByPoints z elementem wyjściowym węzła Surface.PointAtParameter.
2. Można zauważyć, że powstało dziesięć krzywych biegnących pionowo wzdłuż powierzchni.

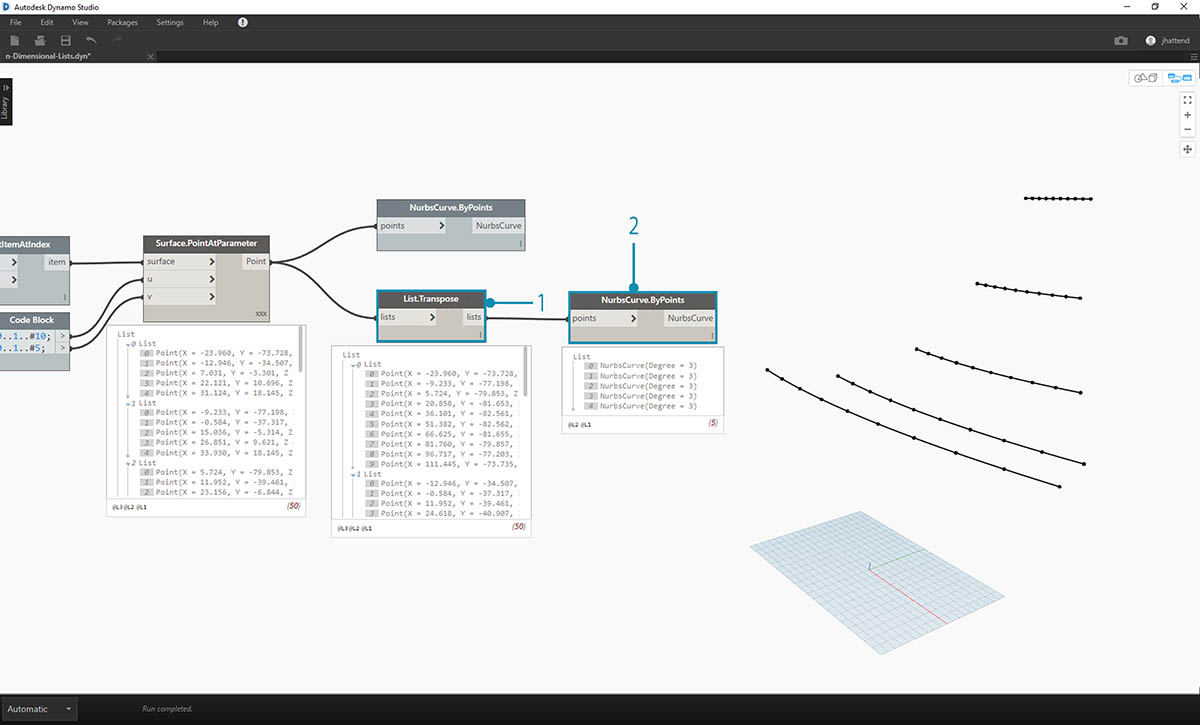
1. Podstawowa funkcja List.Transpose spowoduje zamianę kolumn i wierszy listy list.
2. Po połączeniu elementu wyjściowego węzła List.Transpose z węzłem NurbsCurve.ByPoints powstanie pięć krzywych biegnących poziomo na powierzchni.

Ćwiczenie — listy dwuwymiarowe — zaawansowane

Teraz zwiększmy złożoność. Załóżmy, że chcemy wykonać operację na krzywych utworzonych w poprzednim ćwiczeniu. Możemy na przykład powiązać te krzywe z inną powierzchnią i wykonać pomiędzy nimi wyciągnięcie. To wymaga zwrócenia większej uwagi na strukturę danych, ale podstawowa logika jest taka sama.

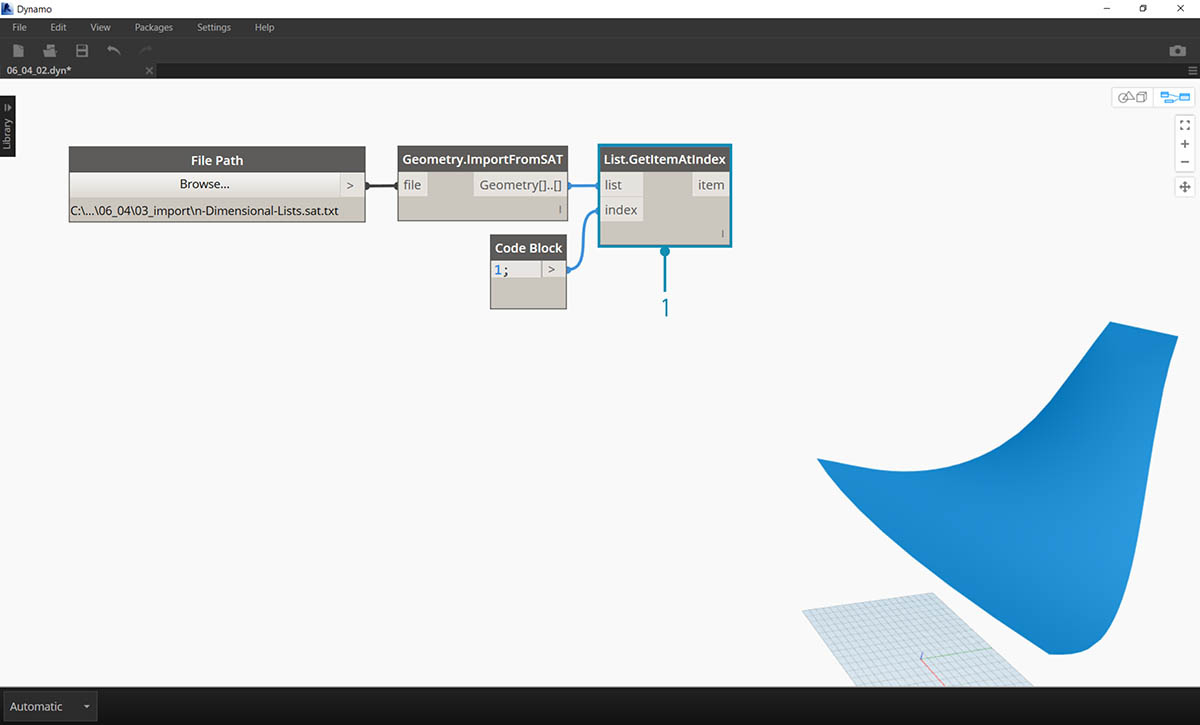
1. Rozpocznij od kroku z poprzedniego ćwiczenia, w którym wyizolowaliśmy górną powierzchnię zaimportowanej geometrii za pomocą węzła List.GetItemAtIndex.

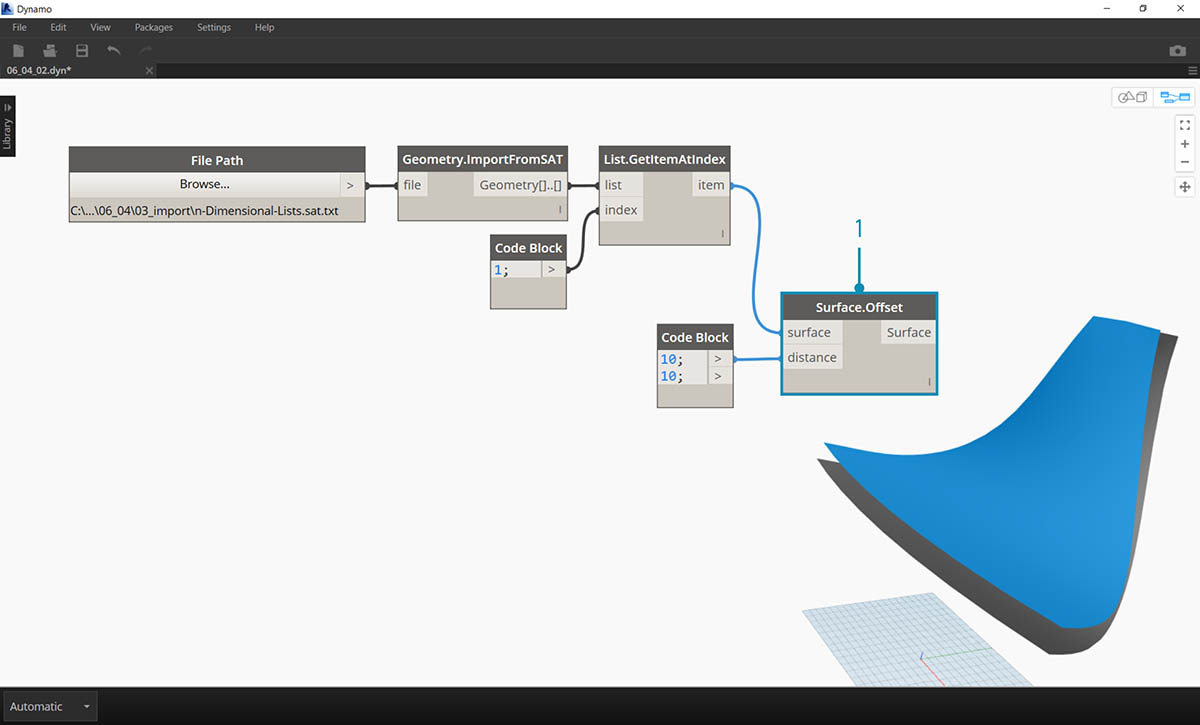
1. Używając węzła Surface.Offset, odsuń tę powierzchnię o wartość 10.

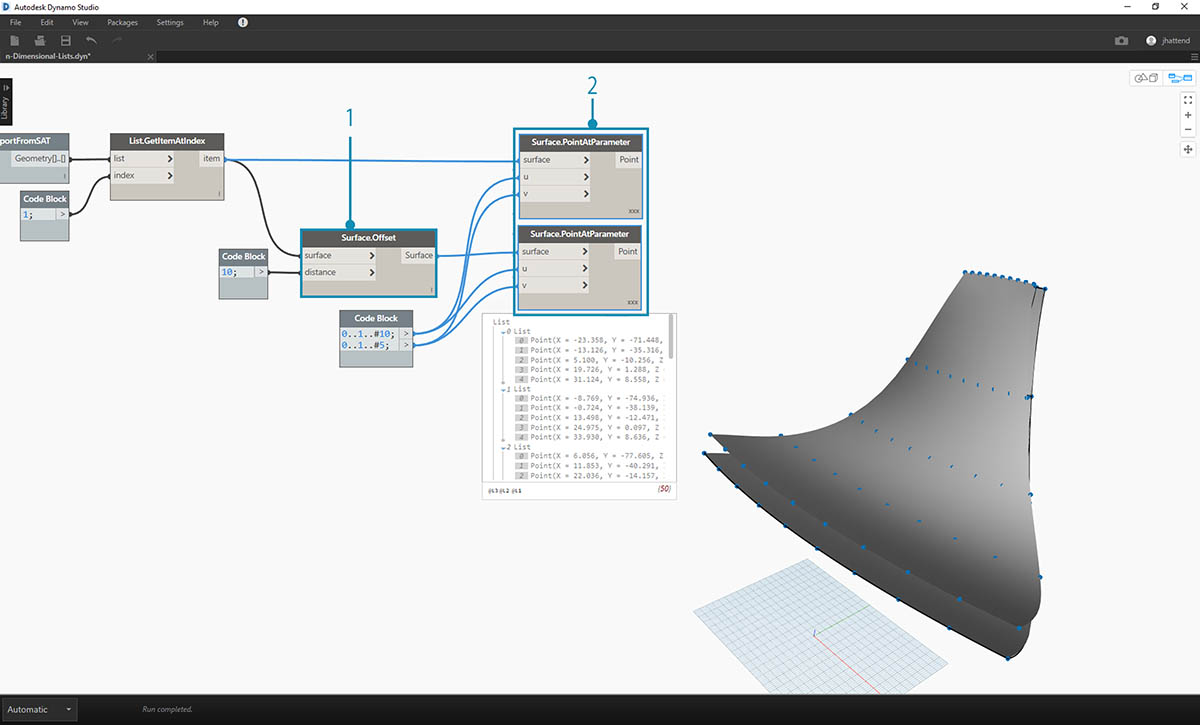
1. Tak samo jak w poprzednim ćwiczeniu, zdefiniuj węzeł Code Block zawierający te dwa wiersze kodu:

   0..1..#10;
   0..1..#5;
   

1. Połącz te dane wyjściowe z dwoma węzłami Surface.PointAtParameter, każdy z opcją skratowania ustawioną na „Iloczyn wektorowy”. Jeden z tych węzłów jest połączony z pierwotną powierzchnią, a drugi z powierzchnią odsuniętą.

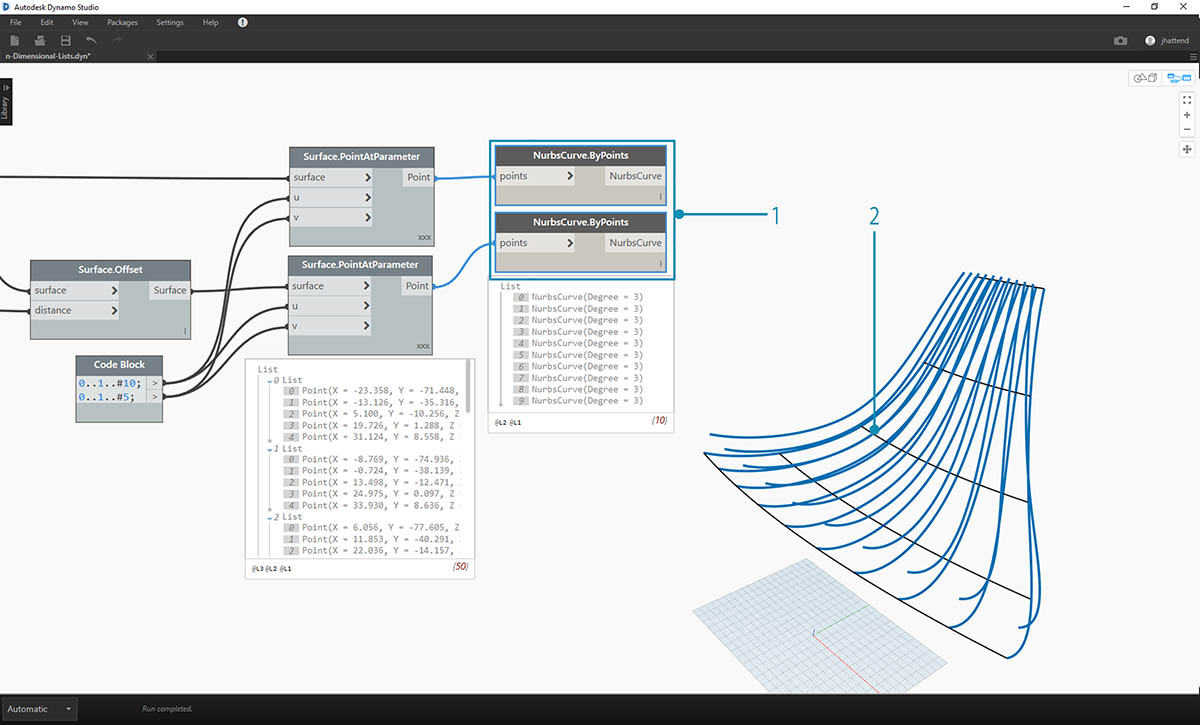
1. Tak samo jak w poprzednim ćwiczeniu, połącz elementy wyjściowe z dwoma węzłami NurbsCurve.ByPoints.
2. W podglądzie dodatku Dynamo wyświetlane są dwie krzywe odpowiadające dwóm powierzchniom.

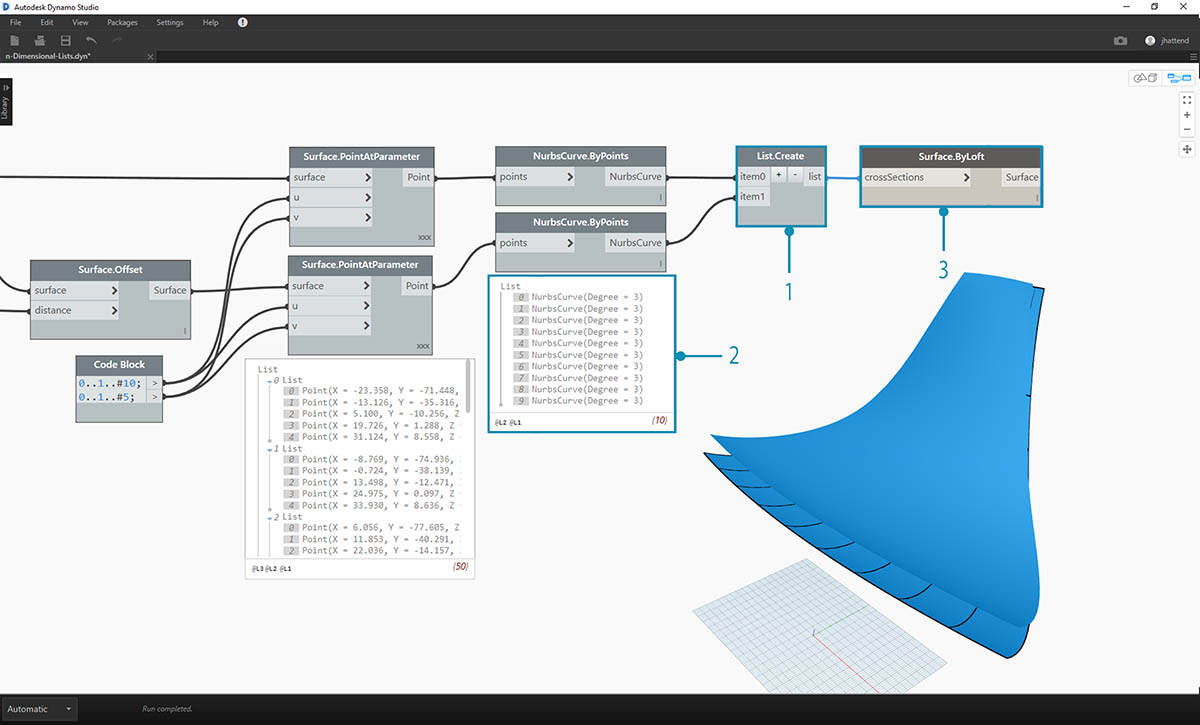
1. Używając węzła List.Create, można połączyć oba zestawy krzywych w jedną listę list.
2. Jak widać w wyniku, otrzymaliśmy dwie listy zawierające po dziesięć elementów, odpowiadające obu połączonym zestawom krzywych NURBS.
3. Wykonując operację Surface.ByLoft, możemy wizualnie zinterpretować tę strukturę danych. Ten węzeł wyciąga wszystkie krzywe na każdej podliście.

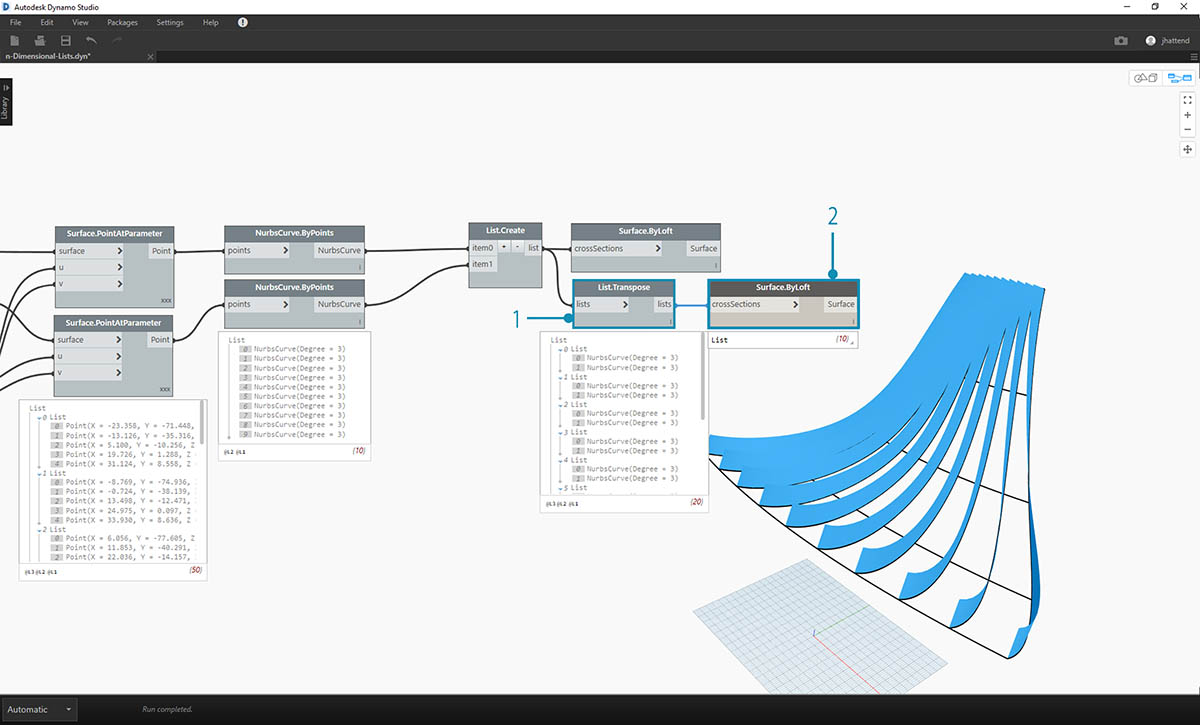
1. Jak pamiętamy, używając węzła List.Transpose, zamieniamy wszystkie kolumny i wiersze. Ten węzeł umożliwia przekształcenie dwóch list po dziesięć krzywych w dziesięć list po dwie krzywe. Teraz każda krzywa NURBS jest powiązana z sąsiednią krzywą na drugiej powierzchni.
2. Po użyciu węzła Surface.ByLoft otrzymujemy żebrowaną strukturę.

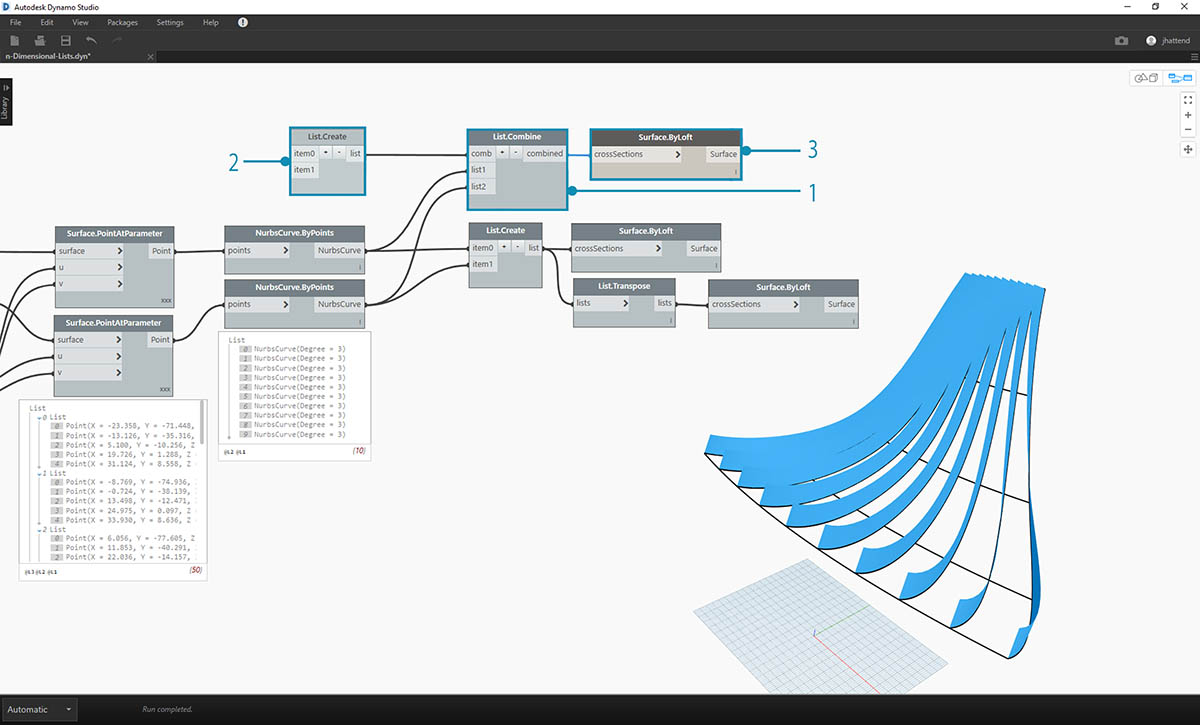
1. Alternatywą dla węzła List.Transpose jest użycie węzła List.Combine. Spowoduje to zastosowanie „kombinatora” do każdej podlisty.
2. W tym przypadku używamy węzła List.Create jako „kombinatora” w celu utworzenia listy dla każdego elementu na podlistach.
3. Po użyciu węzła Surface.ByLoft otrzymujemy takie same powierzchnie, jak w poprzednim kroku. W tym przypadku łatwiej jest użyć węzła Transpose, ale jeśli struktura danych jest jeszcze bardziej złożona, węzeł List.Combine będzie bardziej niezawodny.

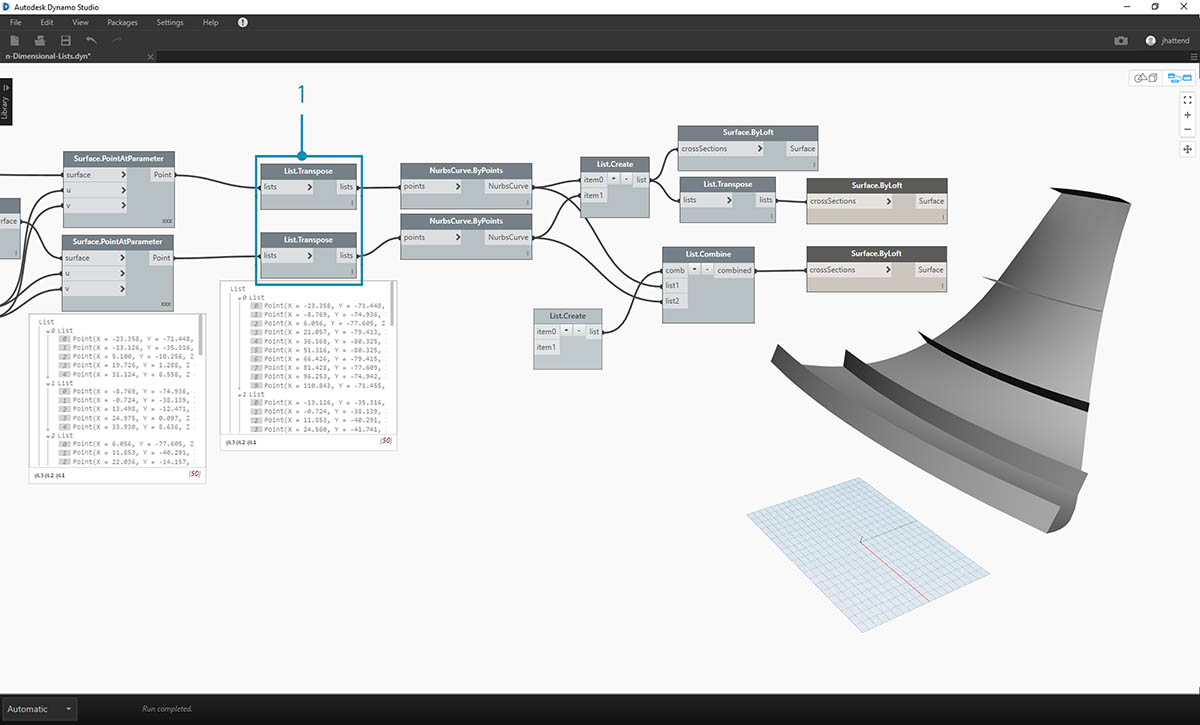
1. Cofając się o kilka kroków, aby zmienić orientację krzywych w żebrowanej strukturze, należy użyć węzła List.Transpose przed połączeniem z węzłem NurbsCurve.ByPoints. Spowoduje to zamianę kolumn i wierszy, dając 5 poziomych żeber.

Ćwiczenie — listy trójwymiarowe

Teraz pójdziemy o krok dalej. W tym ćwiczeniu będziemy pracować z obiema zaimportowanymi powierzchniami, tworząc złożoną hierarchię danych. Będziemy jednak wykonywać tę samą operację z tą samą logiką.

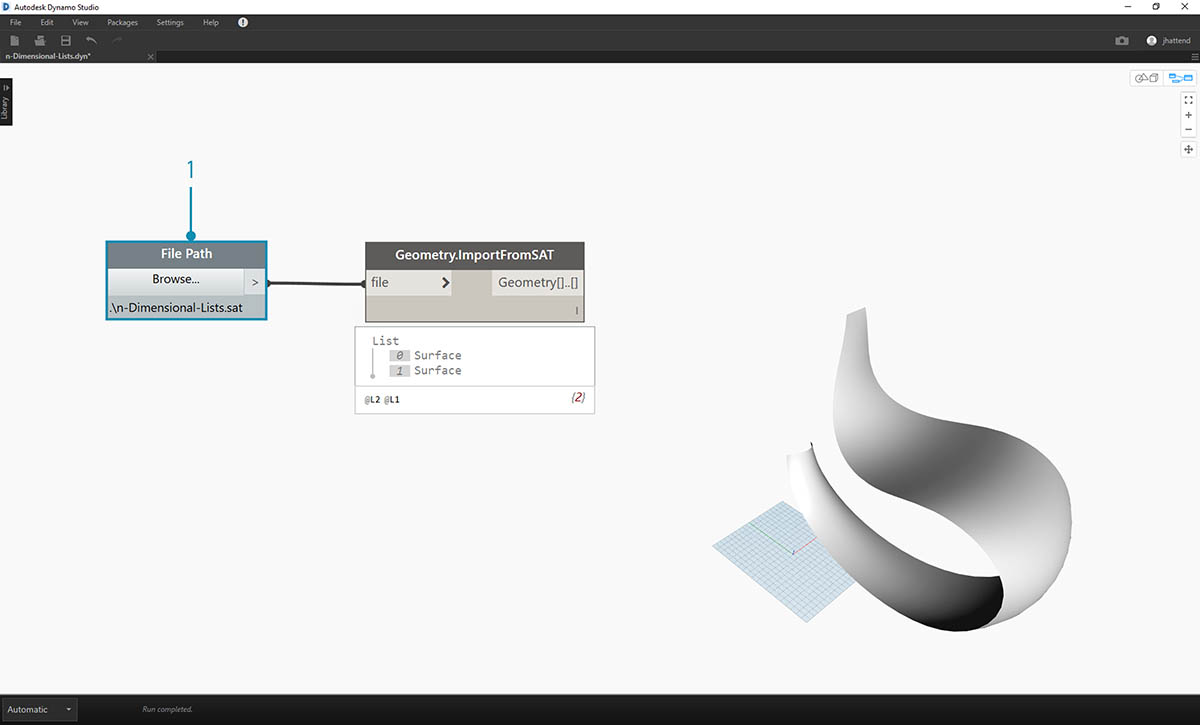
1. Rozpocznij od zaimportowanego pliku z poprzedniego ćwiczenia.

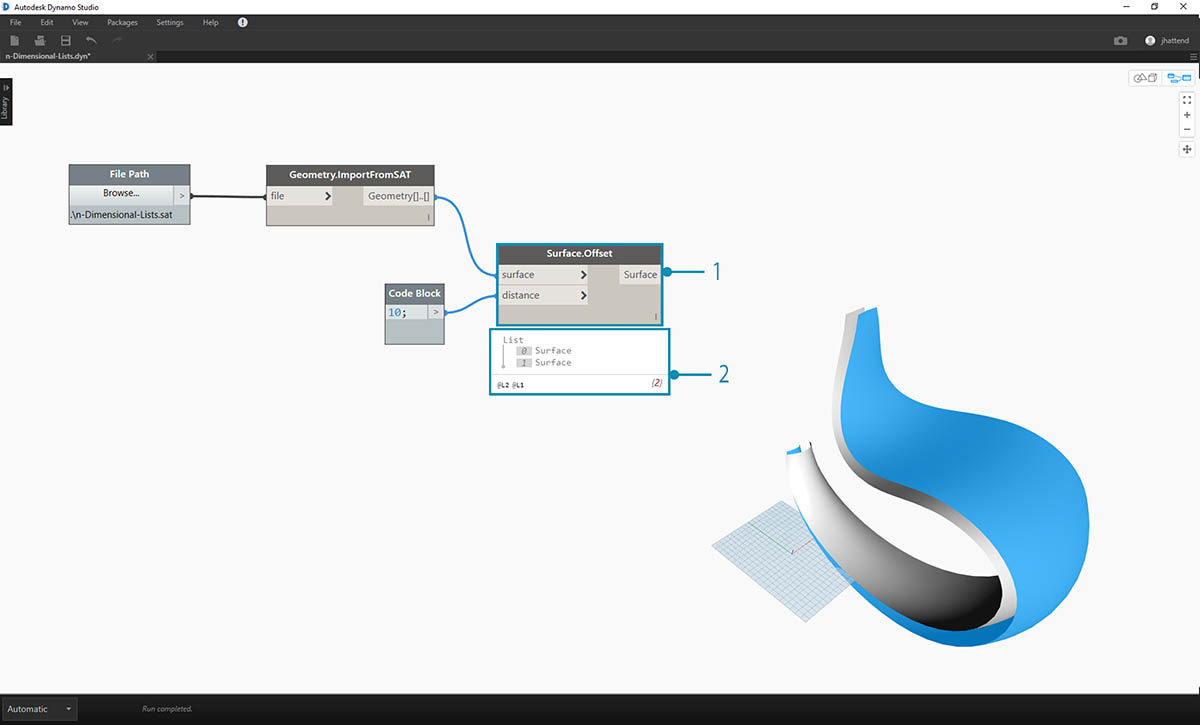
1. Tak samo jak w poprzednim ćwiczeniu, użyj węzła Surface.Offset, aby wykonać odsunięcie o wartość 10.
2. Jak pokazuje wynik, przy użyciu węzła Offset utworzyliśmy dwie powierzchnie.

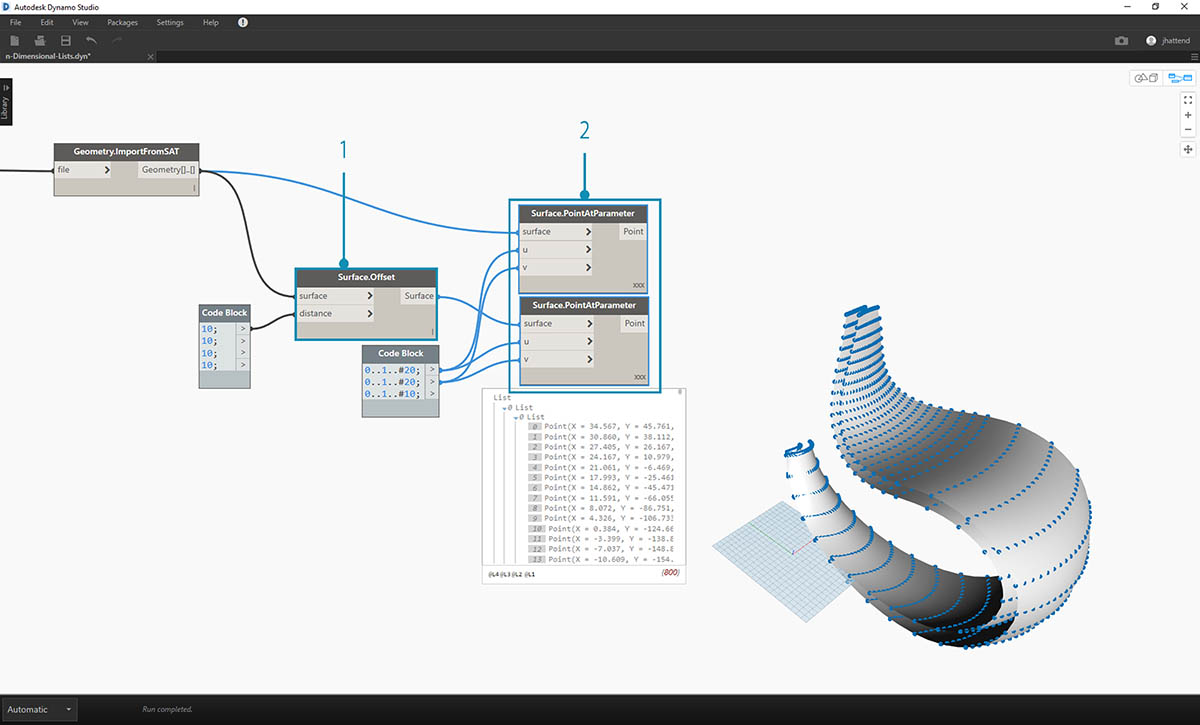
1. Tak samo jak w poprzednim ćwiczeniu, zdefiniuj węzeł Code Block zawierający te dwa wiersze kodu:

   0..1..#20;
   0..1..#10;
   

1. Połącz te dane wyjściowe z dwoma węzłami Surface.PointAtParameter, każdy z opcją skratowania ustawioną na „Iloczyn wektorowy”. Jeden z tych węzłów jest połączony z pierwotnymi powierzchniami, a drugi z powierzchniami odsuniętymi.

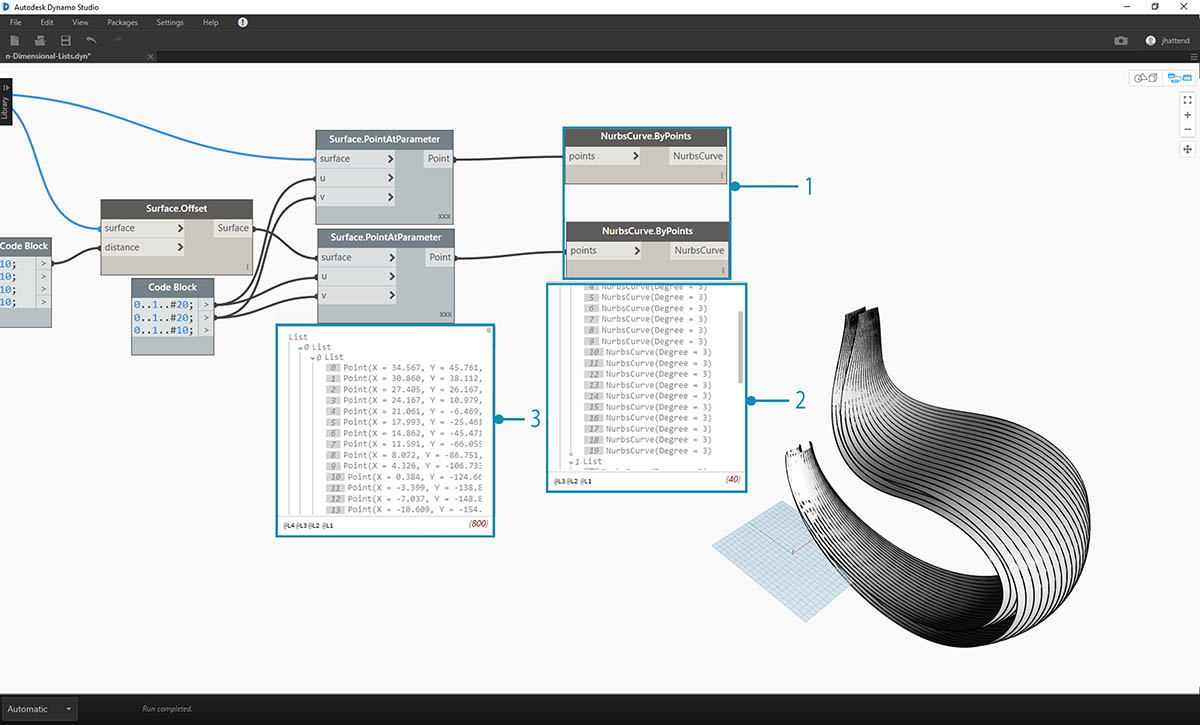
1. Tak samo jak w poprzednim ćwiczeniu, połącz elementy wyjściowe z dwoma węzłami NurbsCurve.ByPoints.
2. W wyniku węzła NurbsCurve.ByPoints widzimy, że jest to lista dwóch list, czyli bardziej złożona struktura niż w poprzednim ćwiczeniu. Dane są kategoryzowane według bazowej powierzchni, a więc dodaliśmy do struktury danych kolejny poziom.
3. Należy zauważyć, że sytuacja w węźle Surface.PointAtParameter się skomplikowała. Mamy już listę list list.

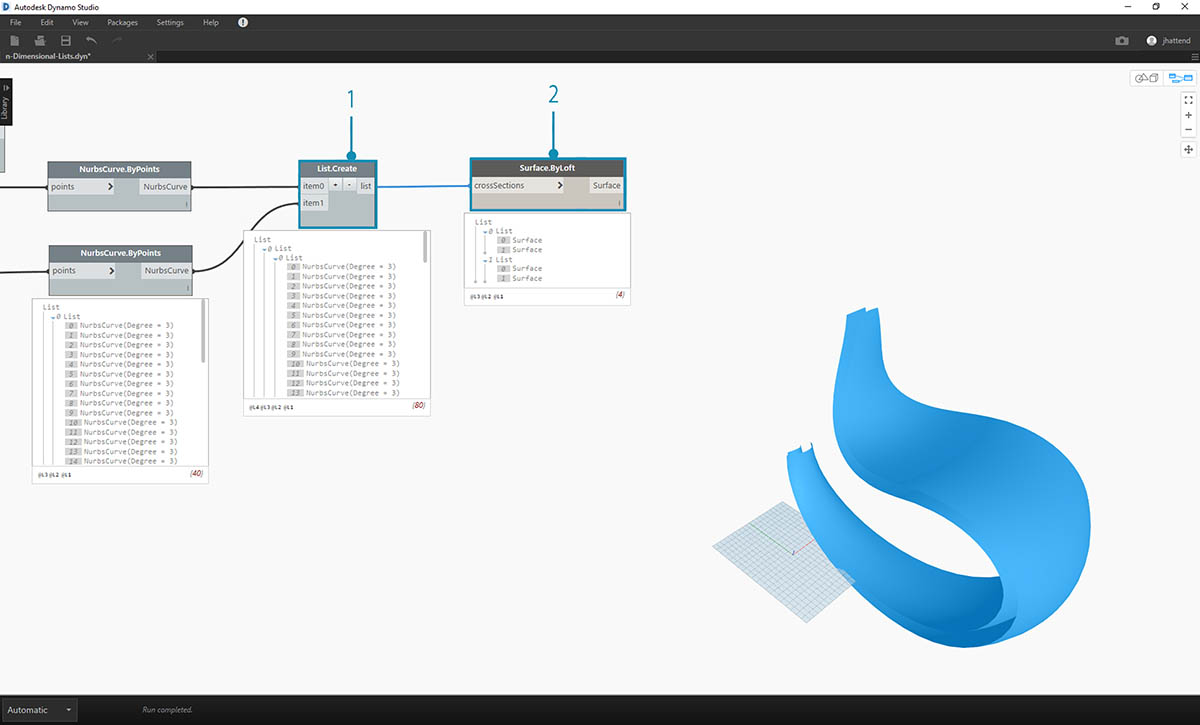
1. Za pomocą węzła List.Create scalamy krzywe NURBS w jedną strukturę danych, tworząc listę list list.
2. Połączenie z węzłem Surface.ByLoft powoduje utworzenie nowej wersji pierwotnych powierzchni, z których każda pozostaje na osobnej liście utworzonej na podstawie początkowej struktury danych.

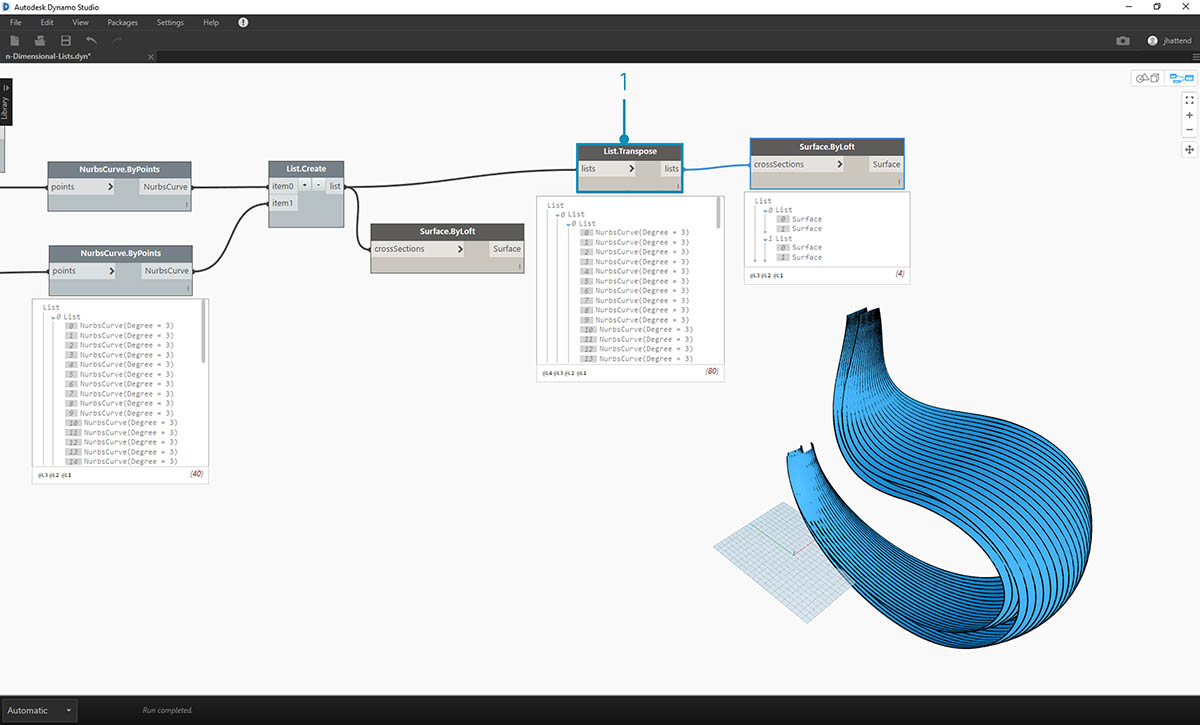
1. W poprzednim ćwiczeniu można było użyć węzła List.Transpose, aby utworzyć żebrowaną strukturę. W tym przypadku to nie zadziała. Transpozycję można stosować do listy dwuwymiarowej, a ponieważ mamy listę trójwymiarową, nie można tak łatwo „zamienić kolumn i wierszy”. Należy pamiętać, że listy to obiekty, a więc węzeł List.Transpose spowodowałby zamianę list z podlistami, ale nie zamianę krzywych NURBS na kolejnym poziomie hierarchii list.

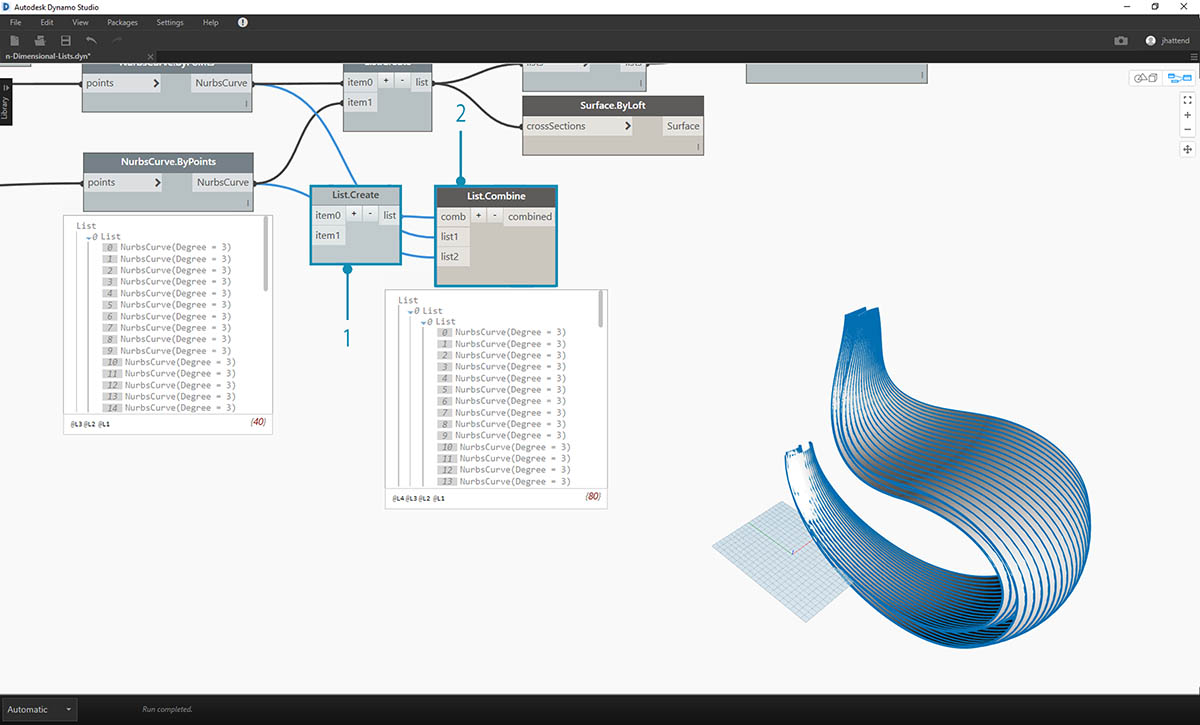
1. W tym przypadku lepiej będzie działać węzeł List.Combine. Przechodząc do bardziej złożonych struktur danych, używamy węzłów List.Map i List.Combine.
2. Używając węzła List.Create jako „kombinatora”, tworzymy strukturę danych, która będzie lepiej przystosowana do naszego celu.

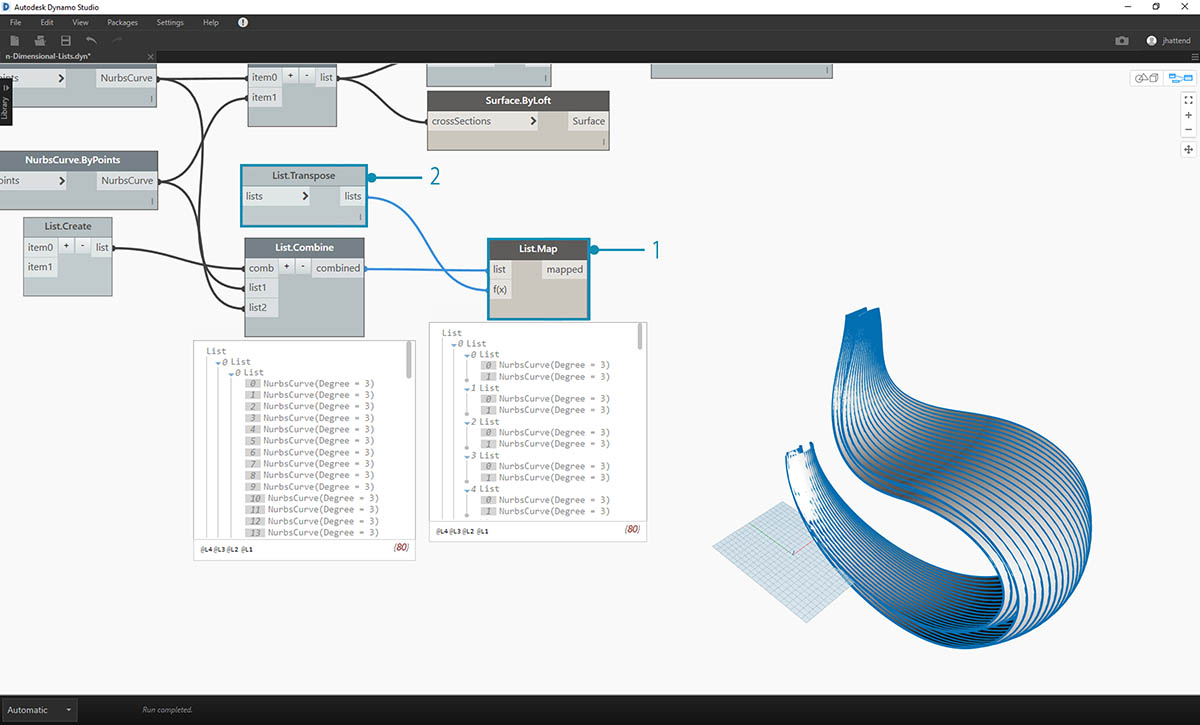
1. Struktura danych wymaga jeszcze transpozycji na niższym poziomie hierarchii. W tym celu użyjemy węzła List.Map. Działa on podobnie jak węzeł List.Combine, ale wymaga jednej listy wejściowej, a nie dwóch lub więcej.
2. Do węzła List.Map zastosujemy funkcję List.Transpose, która spowoduje zamianę kolumn i wierszy podlist na głównej liście.

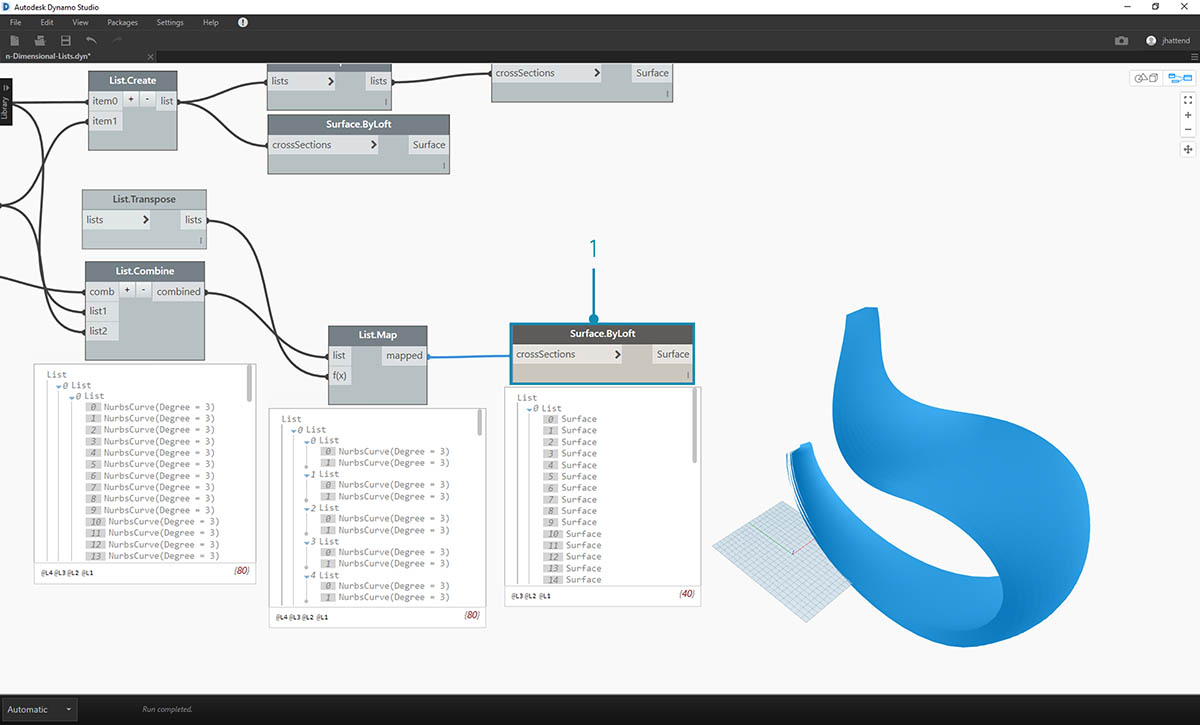
1. Na koniec możemy wyciągnąć krzywe NURBS wraz z odpowiednią hierarchią danych, co daje żebrowaną strukturę.

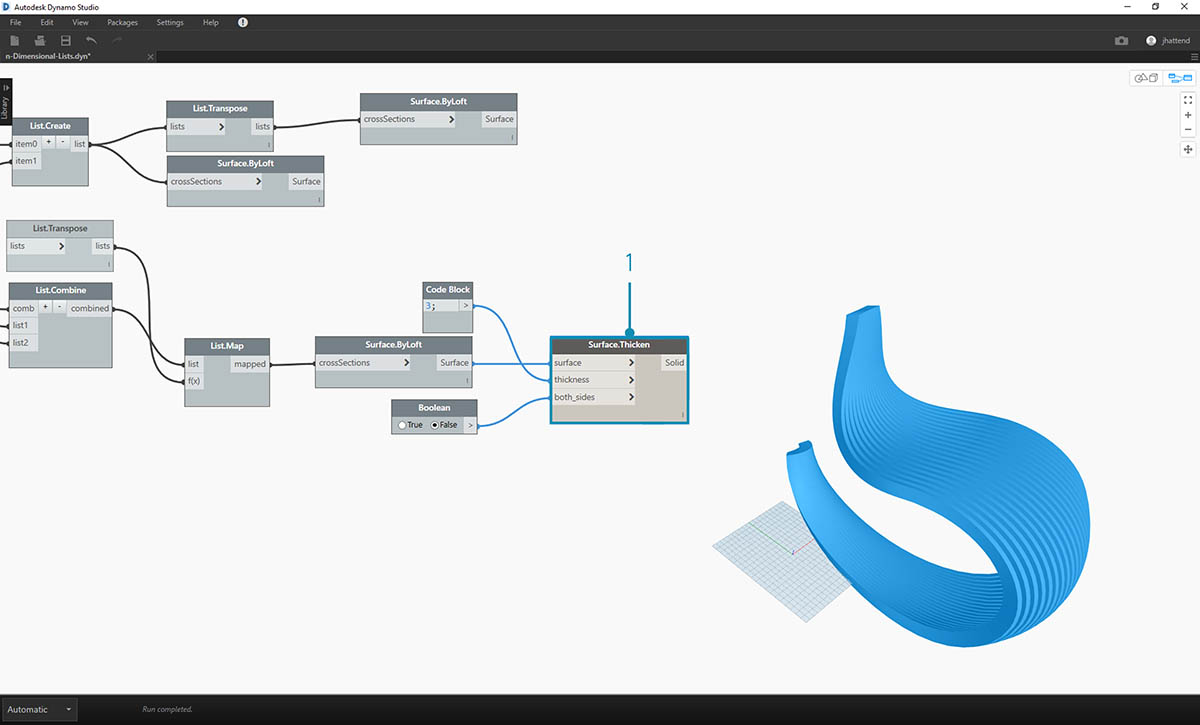
1. Teraz dodamy głębię do tej geometrii za pomocą węzła Surface.Thicken.

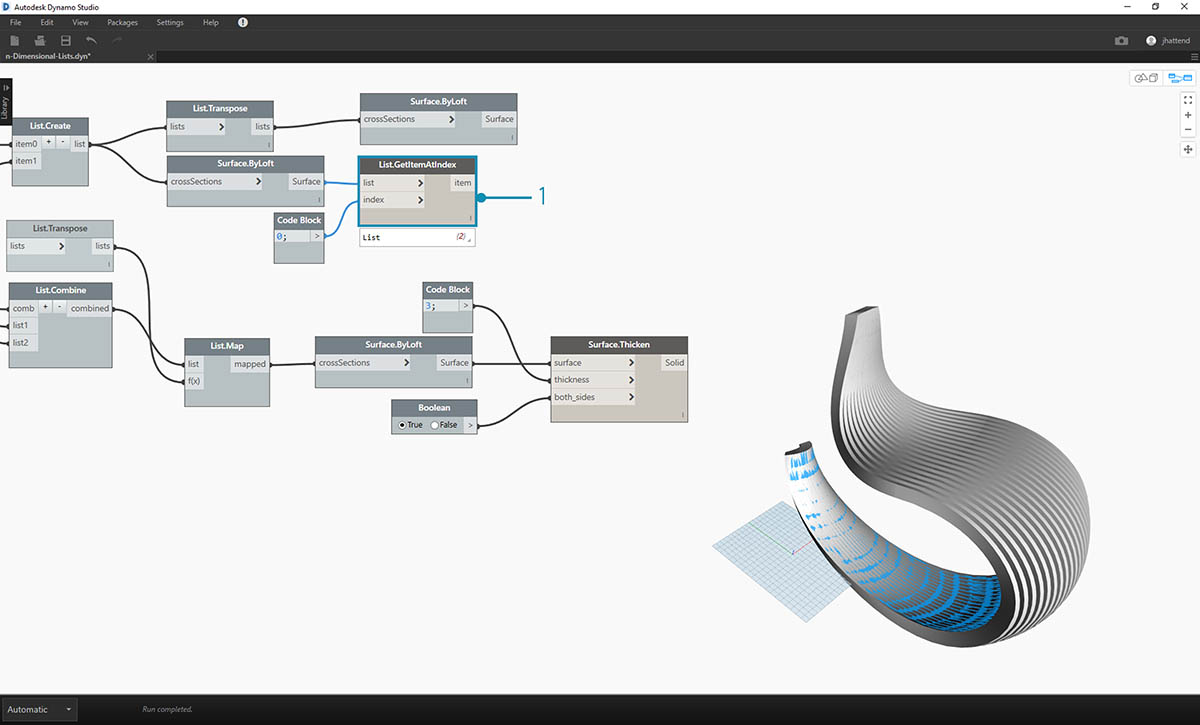
1. Dobrze byłoby dodać powierzchnię jako podparcie tej struktury, dlatego użyjemy węzła List.GetItemAtIndex, aby wybrać tylną powierzchnię z powierzchni wyciągniętych w poprzednich krokach.

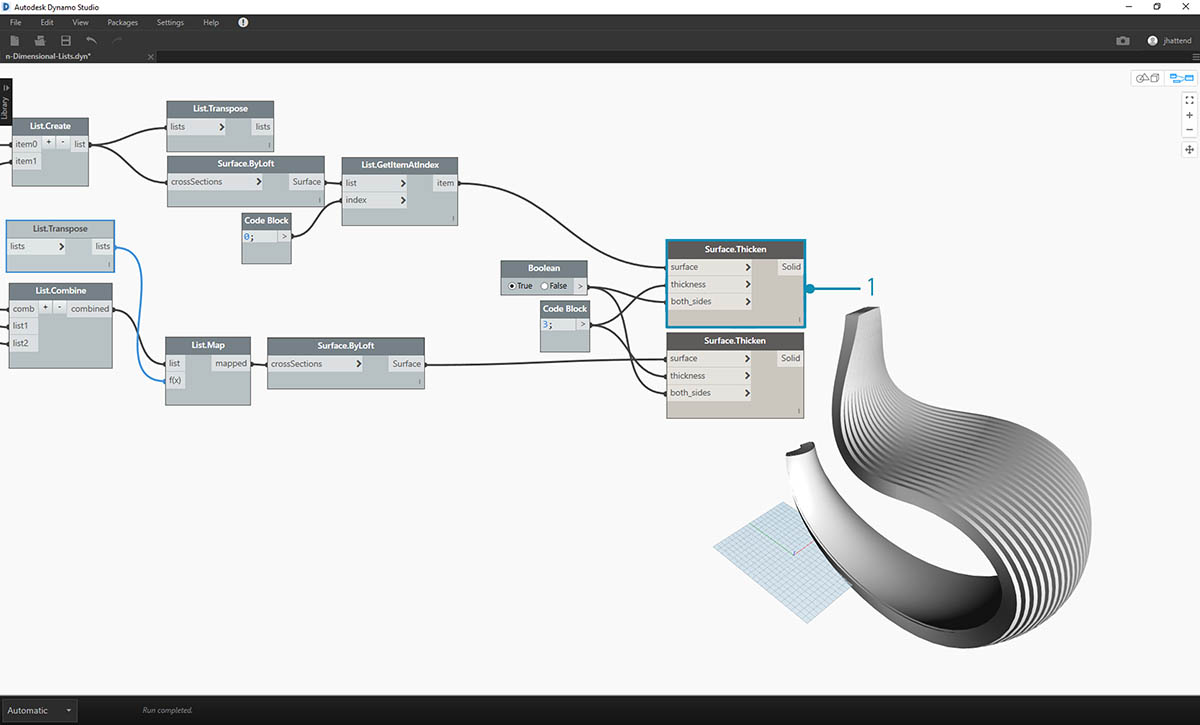
1. Po pogrubieniu wybranych powierzchni artykulacja jest gotowa.

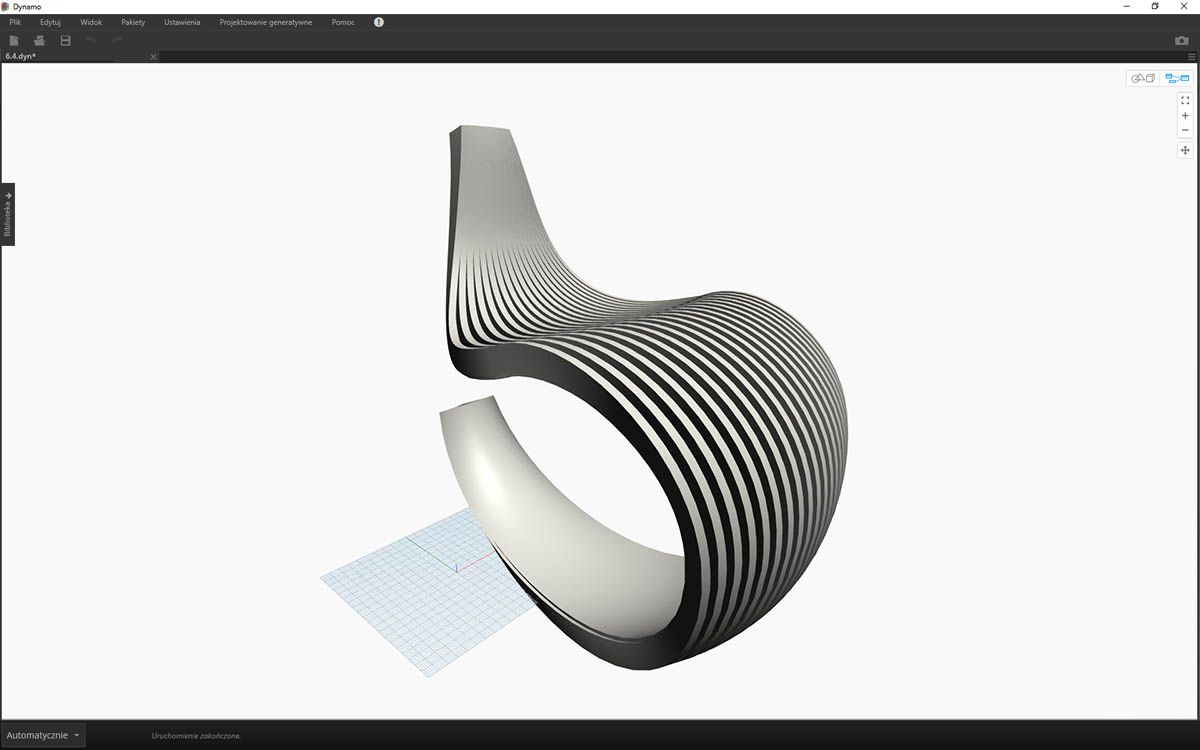
Nie jest to może najwygodniejszy fotel bujany, ale zawiera dużo danych.

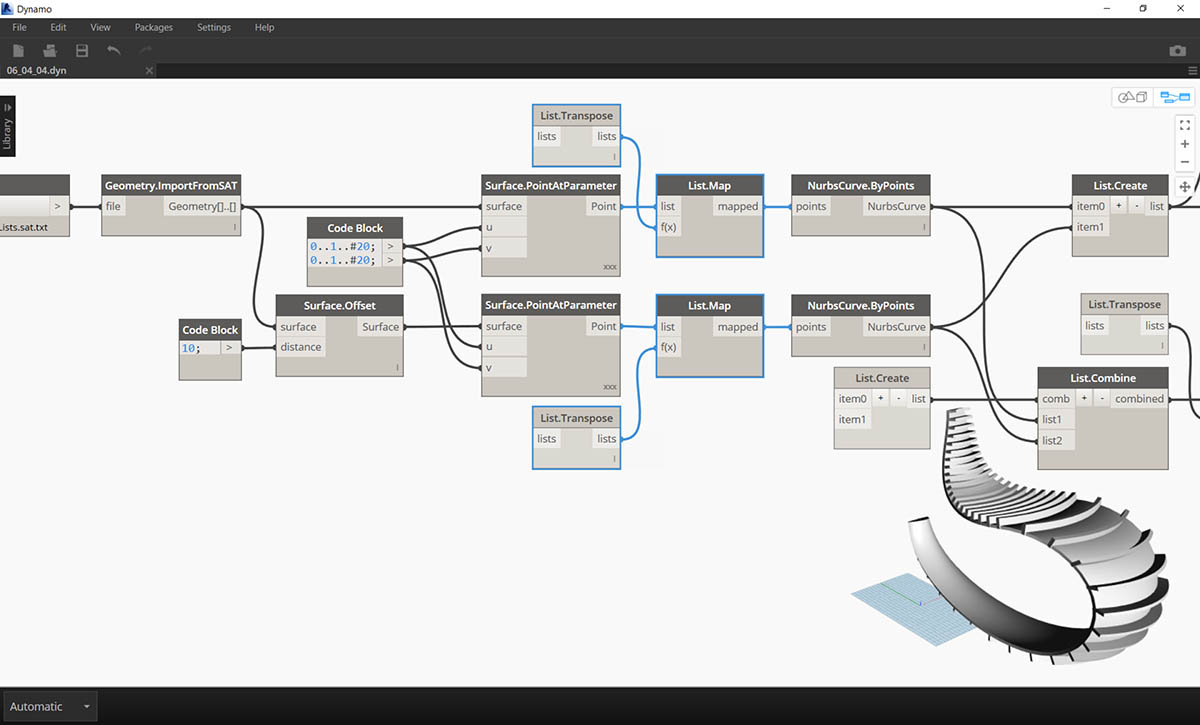
Na ostatnim etapie odwrócimy kierunek prążków. W poprzednim ćwiczeniu stosowaliśmy transpozycję. Tu zrobimy coś podobnego.

1. Ponieważ hierarchia ma jeszcze jeden poziom, należy użyć węzła List.Map z funkcją List.Tranpose, aby zmienić kierunek krzywych NURBS.

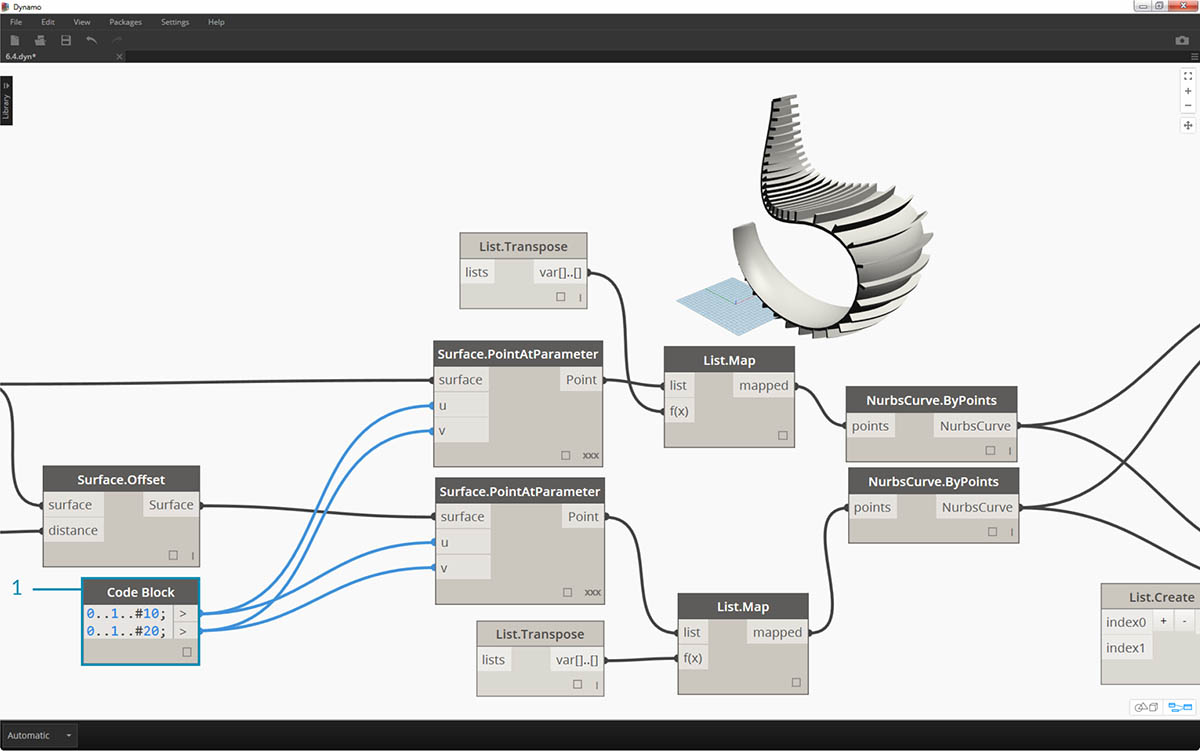
1. Jeśli chcemy zwiększyć liczbę stopni, możemy zmienić blok kodu następująco:

   0..1..#20;
   0..1..#10;
   

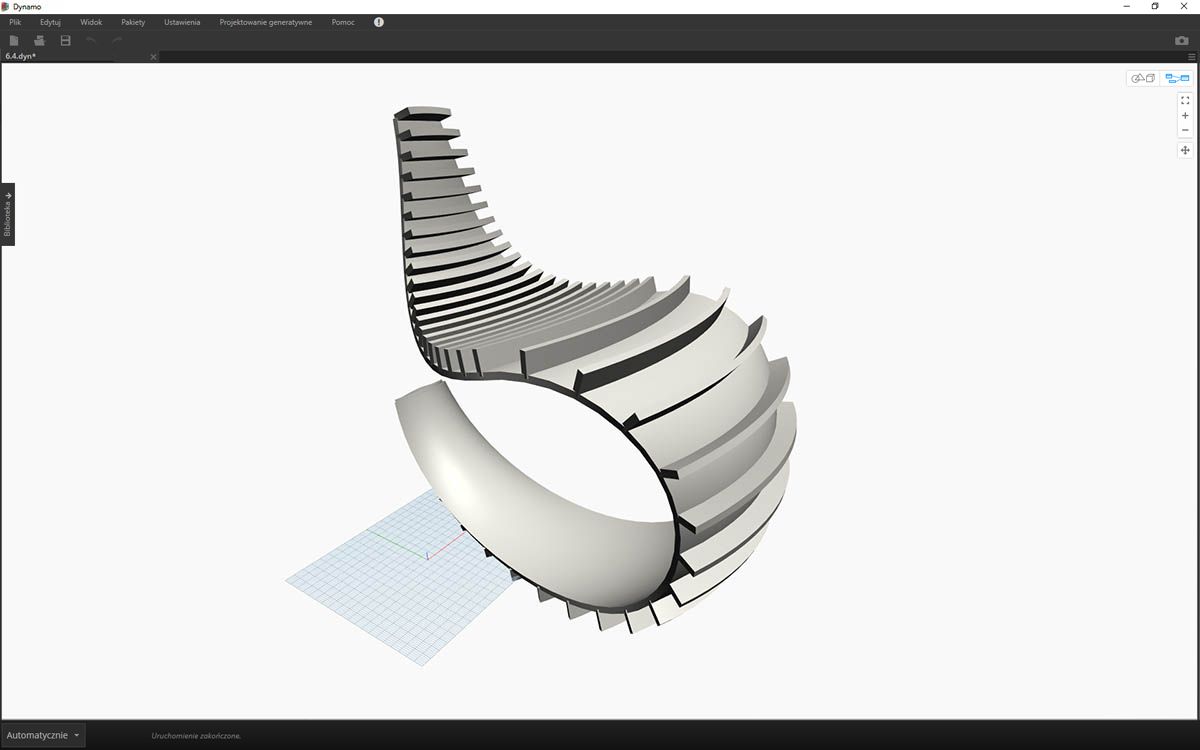
Pierwsza wersja fotela bujanego była bardziej elegancka, a nasz drugi model to wersja dla miłośników sportów ekstremalnych.