Funkcje bloku kodu

W bloku kodu można tworzyć funkcje, a następnie można je ponownie wywoływać w innym miejscu w definicji dodatku Dynamo. Powoduje to utworzenie innej warstwy sterującej w pliku parametrycznym. Można to postrzegać jako wersję tekstową węzła niestandardowego. W tym przypadku „nadrzędny” blok kodu jest łatwo dostępny i może być umieszczony w dowolnym miejscu na wykresie. Nie są potrzebne żadne przewody.

Parent

Pierwszy wiersz zawiera słowo kluczowe „def”, następnie nazwę funkcji, a następnie nazwy danych wejściowych w nawiasach. Klamry definiują treść funkcji. Wartość jest zwracana za pomocą instrukcji „return =”. Bloki kodu, które definiują funkcję, nie mają portów wejściowych ani wyjściowych, ponieważ są wywoływane z innych bloków kodu.

/*This is a multi-line comment,
which continues for
multiple lines*/
def FunctionName(in1,in2)
{
//This is a comment
sum = in1+in2;
return sum;
};

Podrzędne

Wywołaj funkcję w innym bloku kodu w tym samym pliku przez podanie nazwy i takiej samej liczby argumentów. Działa to tak jak w przypadku gotowych węzłów w bibliotece.

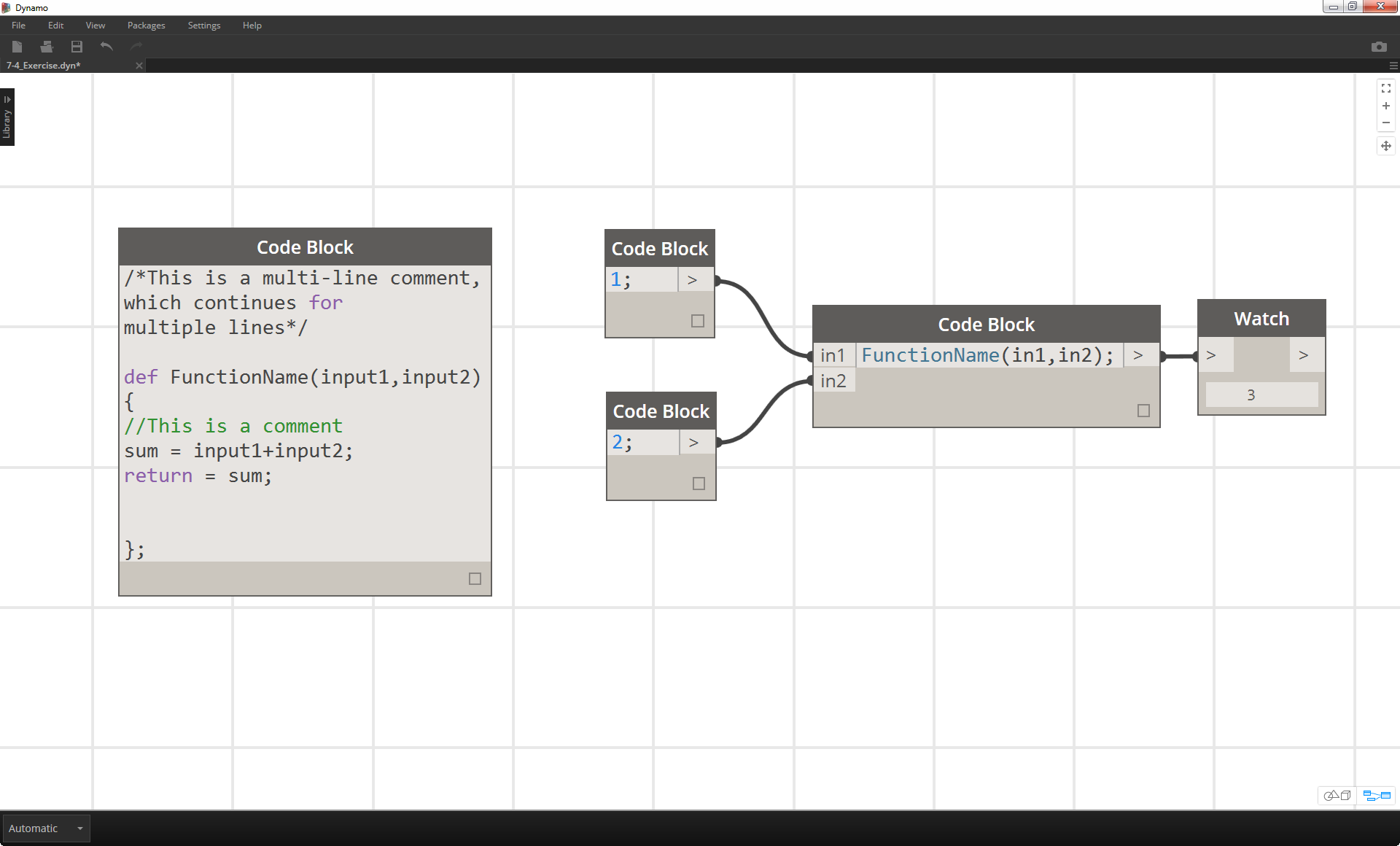
FunctionName(in1,in2);

Ćwiczenie

Pobierz plik przykładowy do tego ćwiczenia (kliknij prawym przyciskiem myszy i wybierz polecenie Zapisz element docelowy jako). Pełna lista plików przykładowych znajduje się w załączniku. Functions_SphereByZ.dyn

W tym ćwiczeniu zostanie utworzona ogólna definicja, która utworzy sfery z wejściowej listy punktów. Promień tych sfer zależy od właściwości Z każdego punktu.

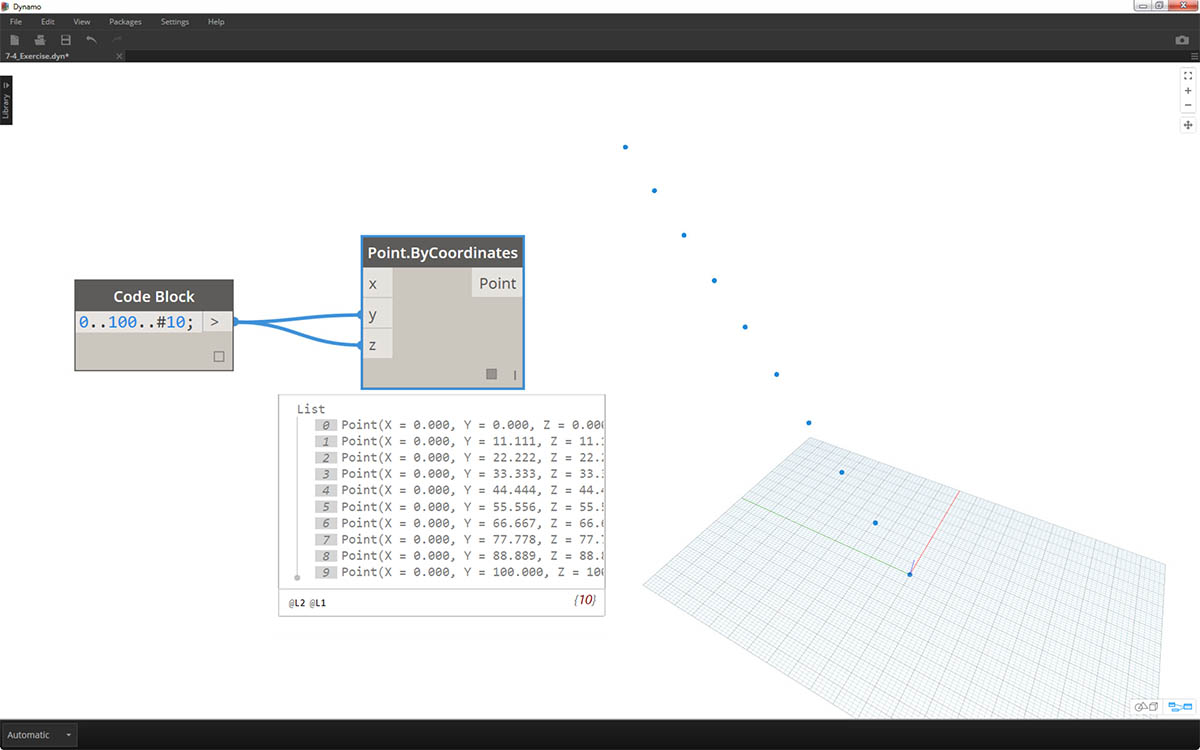
Zacznijmy od przedziału liczbowego dziesięciu wartości z zakresu od 0 do 100. Podłącz je do węzłów Point.ByCoordinates, aby utworzyć linię przekątną.

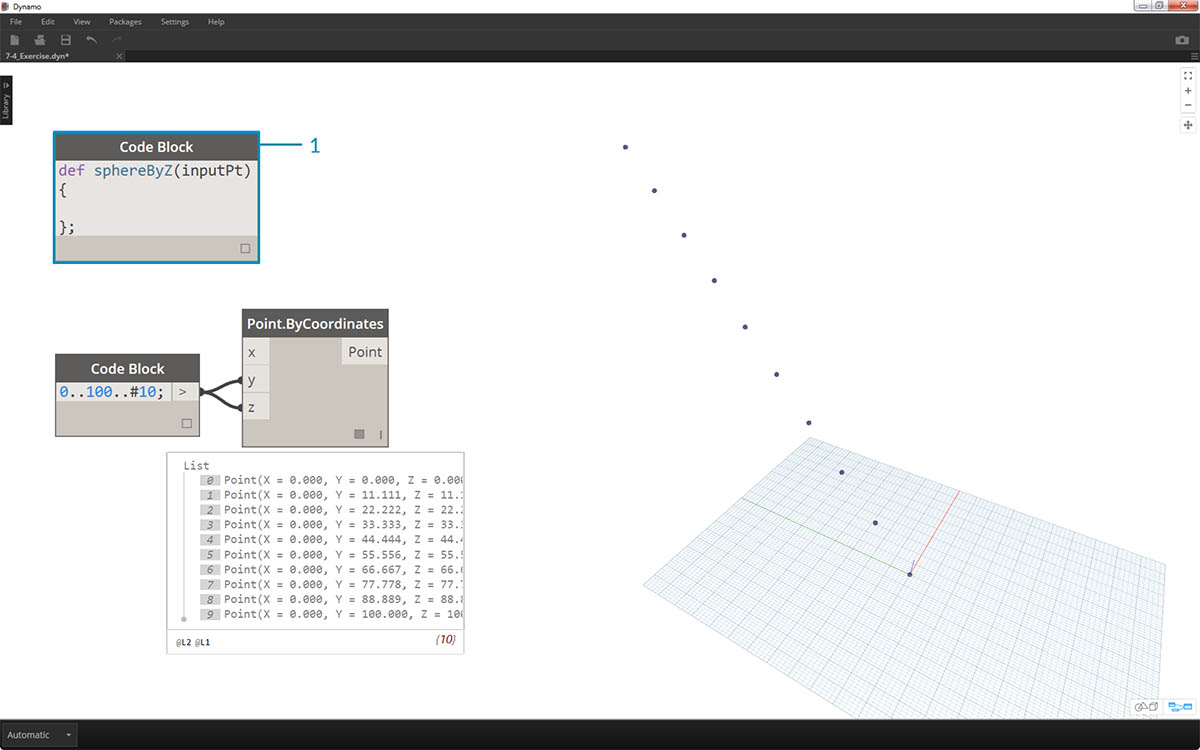
1. Utwórz blok kodu i wprowadź definicję za pomocą wiersza kodu:

   def sphereByZ(inputPt){
   };
   

inputPt to nazwa, którą nadaliśmy reprezentacji punktów sterujących funkcją. Na razie funkcja niczego nie robi, ale w kolejnych krokach ją skonstruujemy.

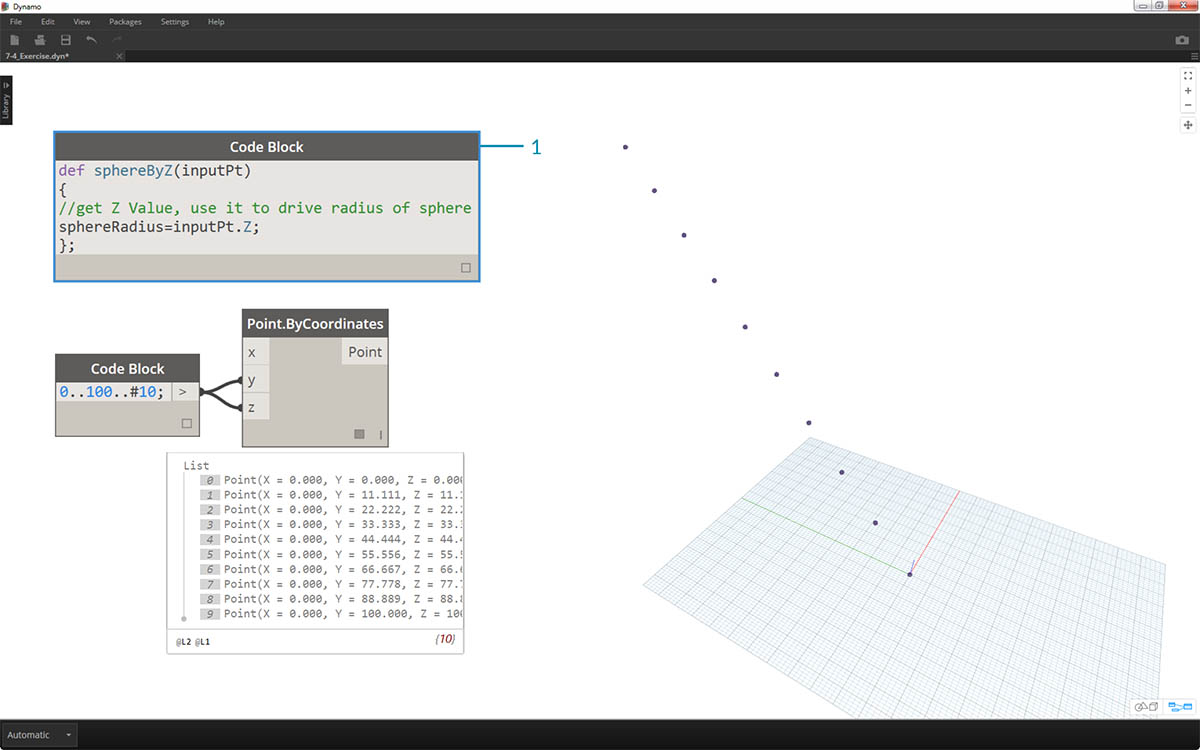
1. Dodając elementy do funkcji bloku kodu, umieścimy komentarz i zmienną sphereRadius, która wysyła zapytanie o położenie Z każdego punktu. Pamiętaj, że inputPt.Z nie wymaga nawiasów jak metoda. Jest to zapytanie o właściwości istniejącego elementu, dlatego żadne dane wejściowe nie są konieczne:

   def sphereByZ(inputPt,radiusRatio)
   {
   //get Z Value, use it to drive radius of sphere
   sphereRadius=inputPt.Z;
   };
   

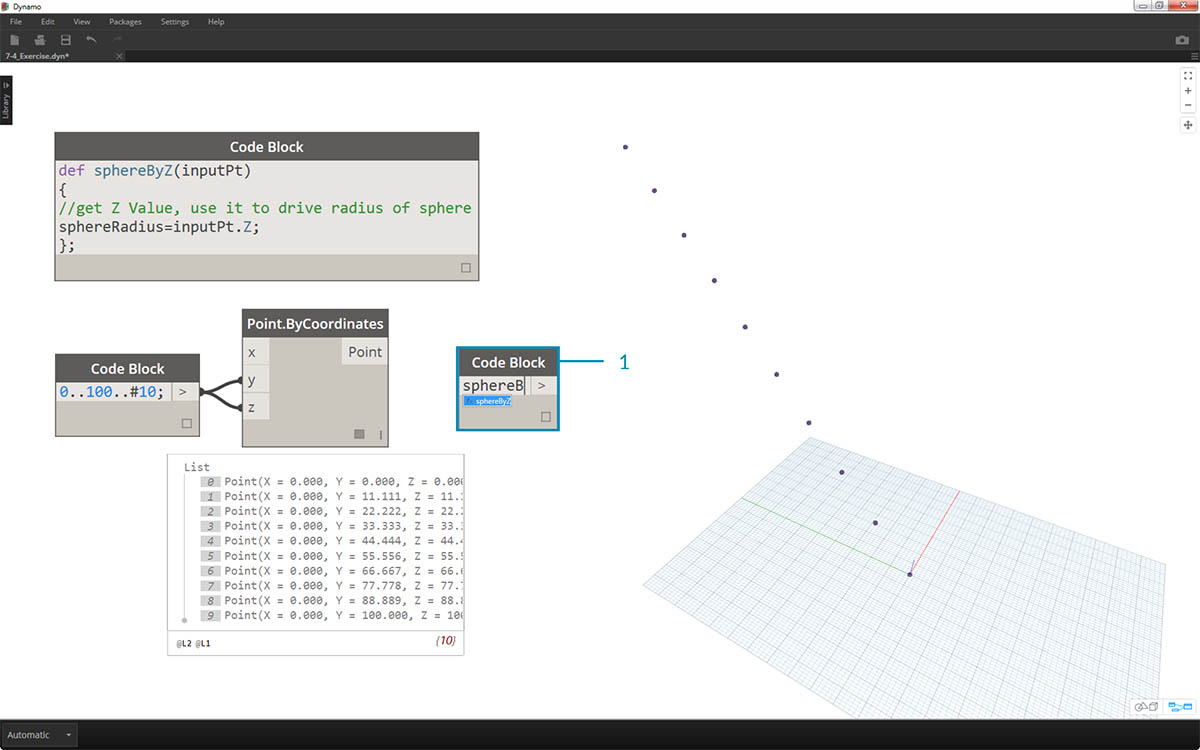
1. Teraz przypomnijmy sobie funkcję, którą utworzyliśmy w innym bloku kodu. Jeśli dwukrotnie klikniemy obszar roboczy, aby utworzyć nowy blok kodu, i wpiszemy sphereB, dodatek Dynamo zasugeruje zdefiniowaną przez nas wcześniej funkcję sphereByZ. Funkcja została dodana do biblioteki intellisense. To przydatne.

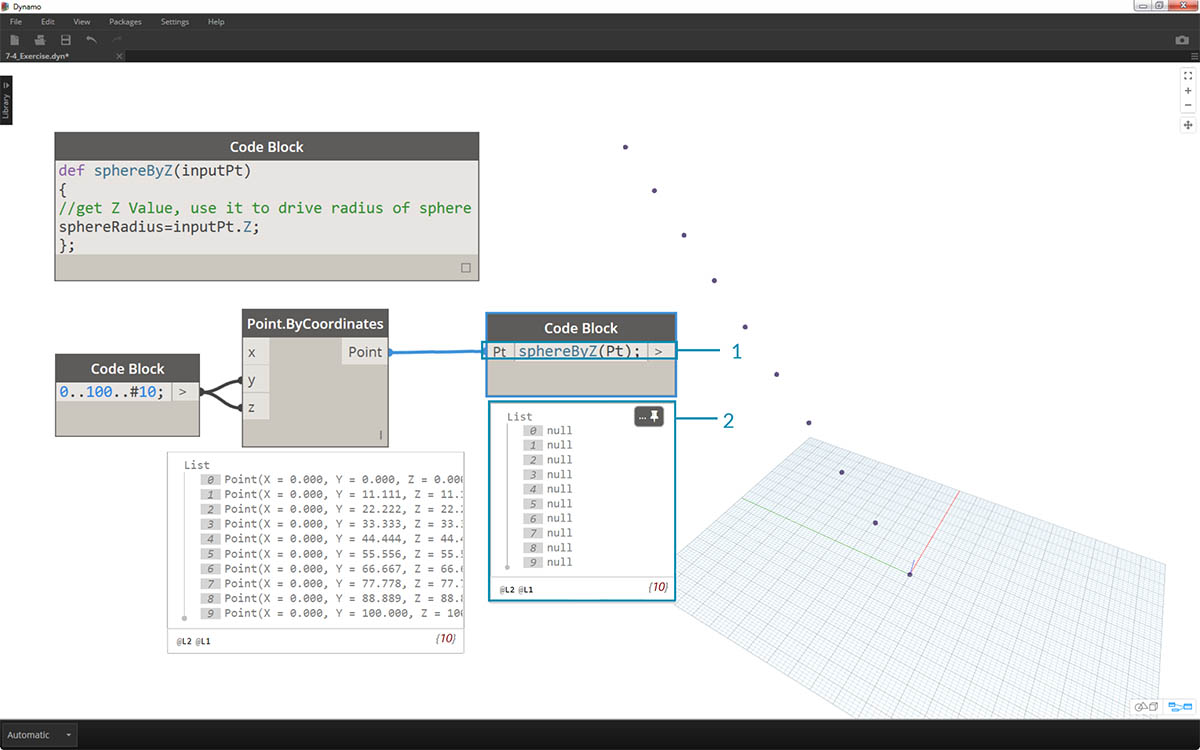
1. Teraz wywołamy tę funkcję i utworzymy zmienną o nazwie Pt, aby podłączyć punkty utworzone w poprzednich krokach:

   sphereByZ(Pt)
   

1. Wszystkie wyjścia mają wartości null. Dlaczego tak jest? W definicji funkcji obliczamy zmienną sphereRadius, ale nie zdefiniowaliśmy, co funkcja powinna zwracać na wyjściu. Możemy to naprawić w następnym kroku.

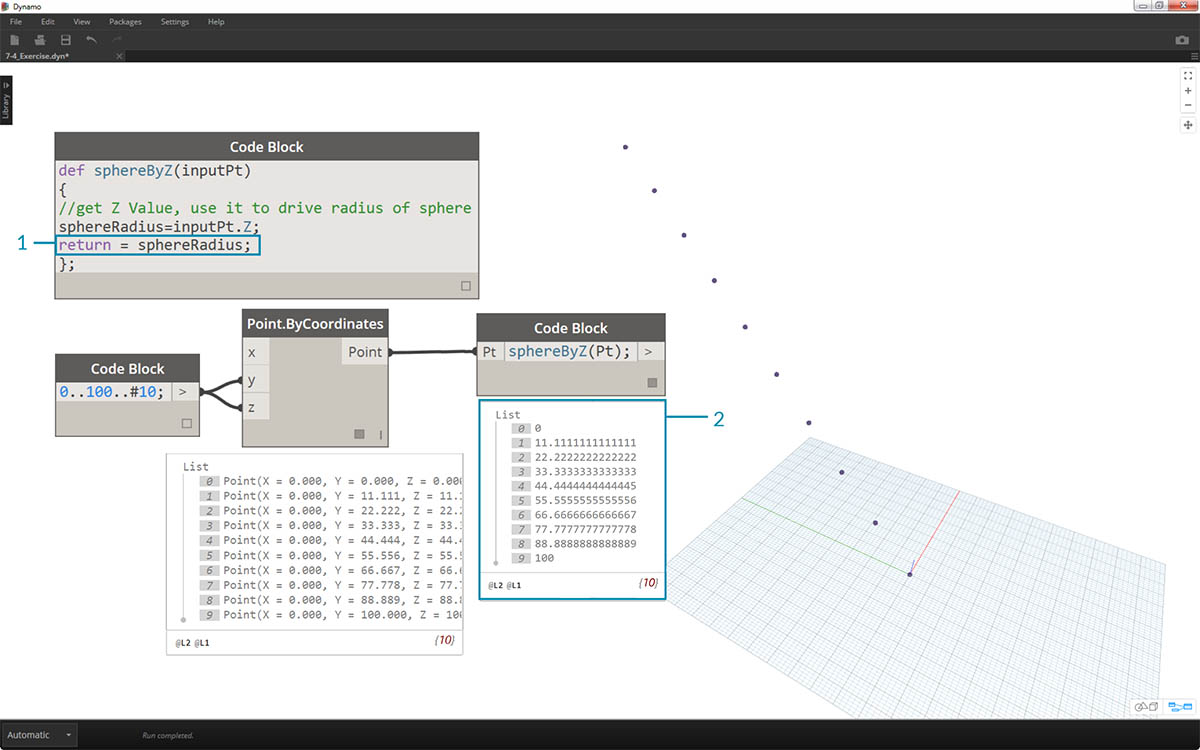
1. Ważnym krokiem jest zdefiniowanie wyjścia funkcji przez dodanie wiersza return = sphereRadius; do funkcji sphereByZ.
2. Teraz na wyjściu bloku kodu pojawiają się współrzędne Z każdego punktu.

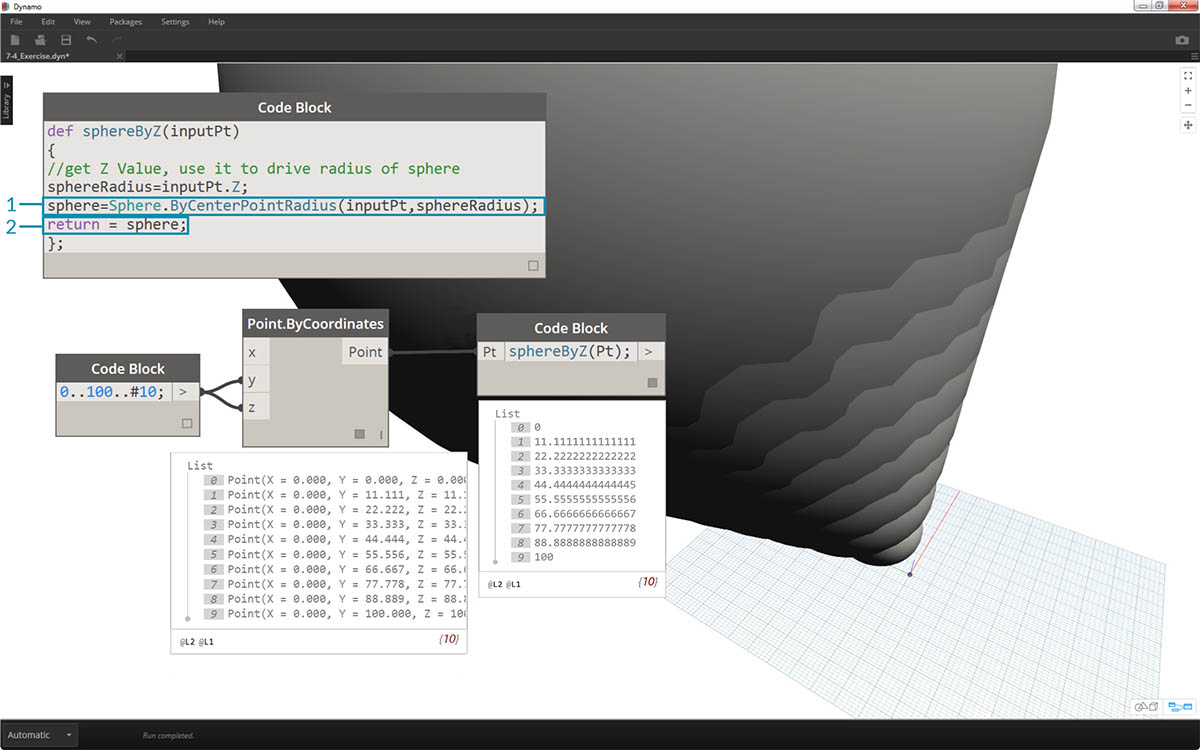
Teraz utworzymy właściwe sfery, edytując funkcję nadrzędną.

1. Najpierw zdefiniujemy sferę za pomocą wiersza kodu: sphere=Sphere.ByCenterPointRadius(inputPt,sphereRadius);
2. Następnie zmienimy zwracaną wartość na sphere zamiast sphereRadius: return = sphere;. To pozwoli nam uzyskać kilka gigantycznych sfer w podglądzie Dynamo.

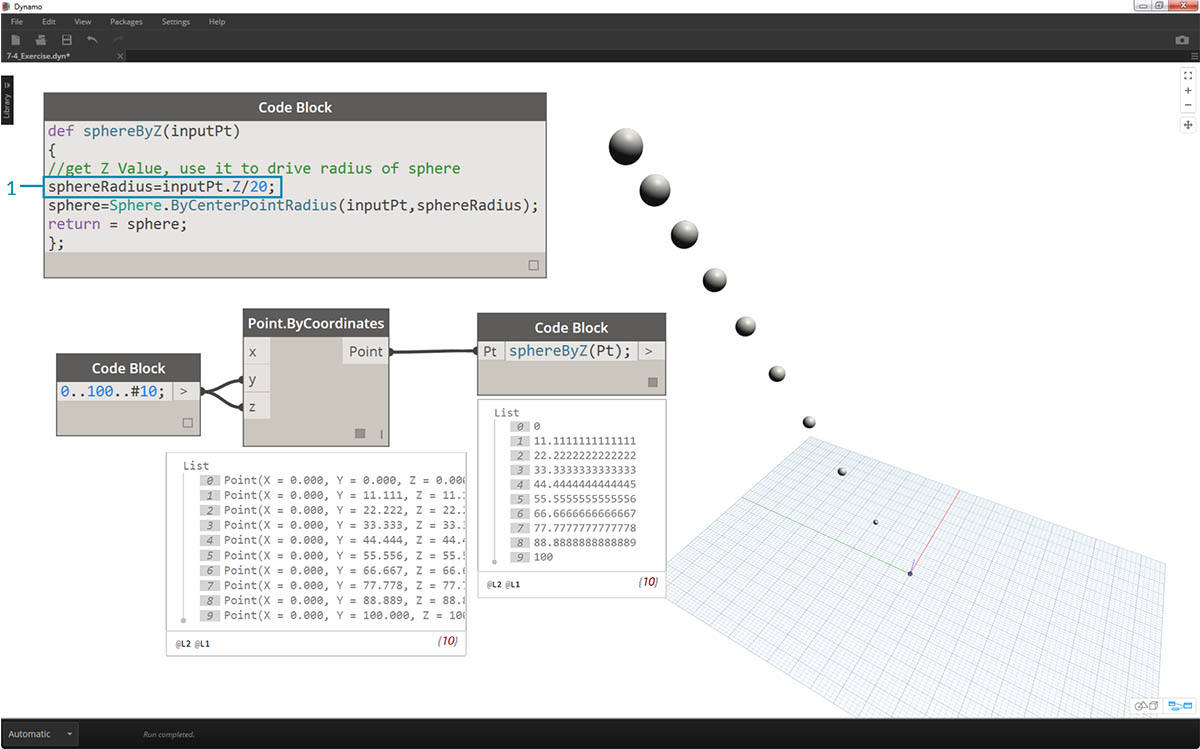
1. Aby zwiększyć rozmiar tych sfer, zaktualizuj wartość sphereRadius, dodając dzielnik: sphereRadius = inputPt.Z/20;. Teraz możemy dostrzec osobne sfery i zrozumieć związek między wartością promienia a wartością Z.

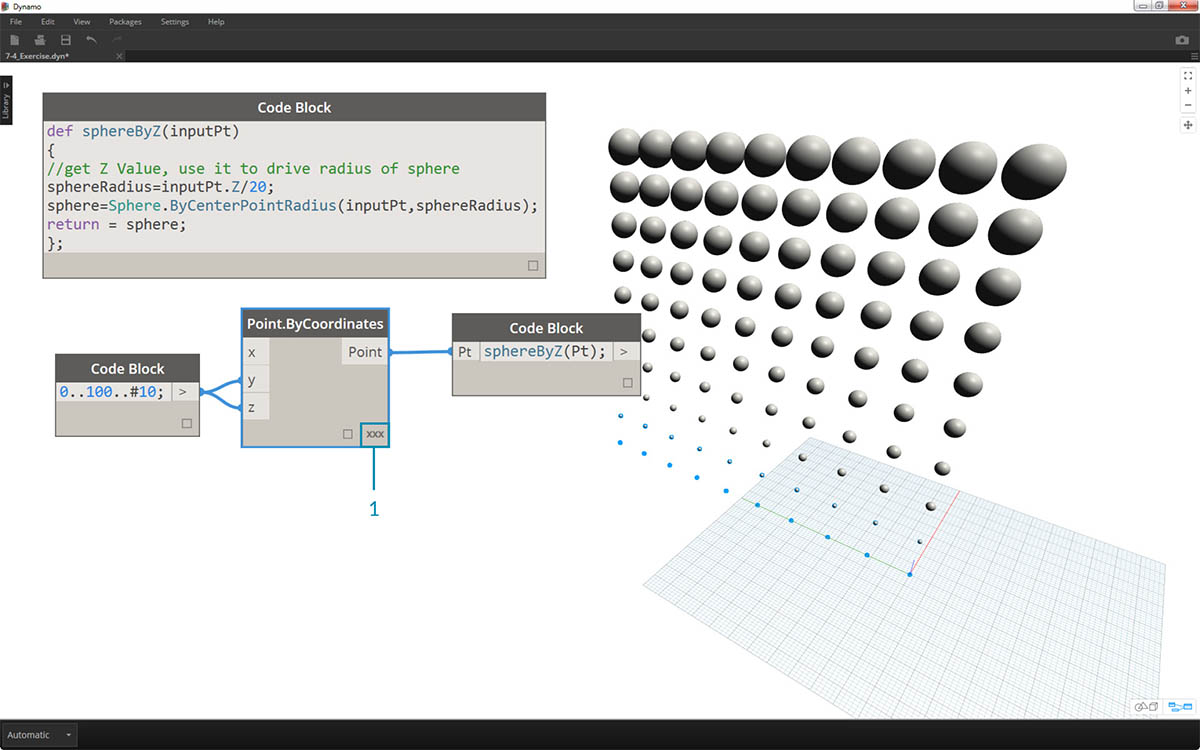
1. W węźle Point.ByCoordinates tworzymy siatkę punktów, zmieniając skratowanie z Shortest List (Najkrótsza lista) na Cross Product (Iloczyn kartezjański). Funkcja sphereByZ nadal w pełni działa, dlatego wszystkie punkty tworzą sfery z promieniami na podstawie wartości Z.

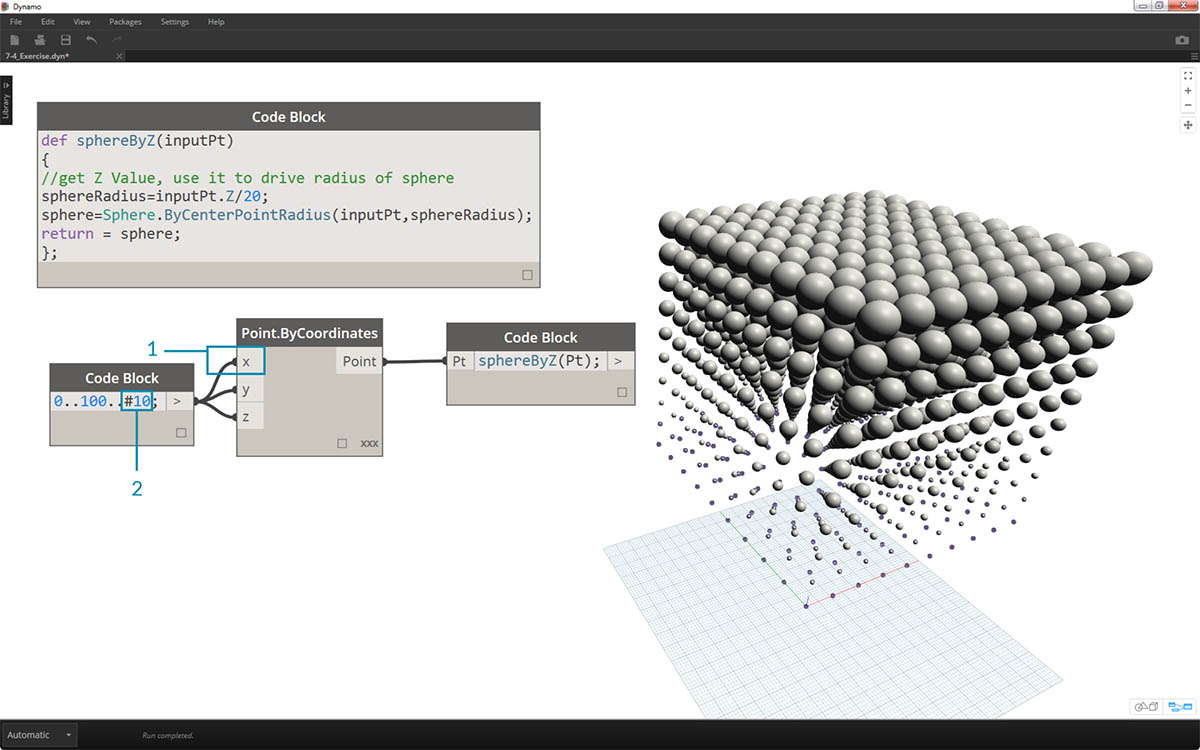
1. Aby przetestować rozwiązanie, podłączymy oryginalną listę liczb do wejść X węzła Point.ByCoordinates. Mamy teraz sześcian sfer.
2. Uwaga: jeśli obliczenia na komputerze trwają długo, spróbuj zmienić #10 na wartość typu #5.

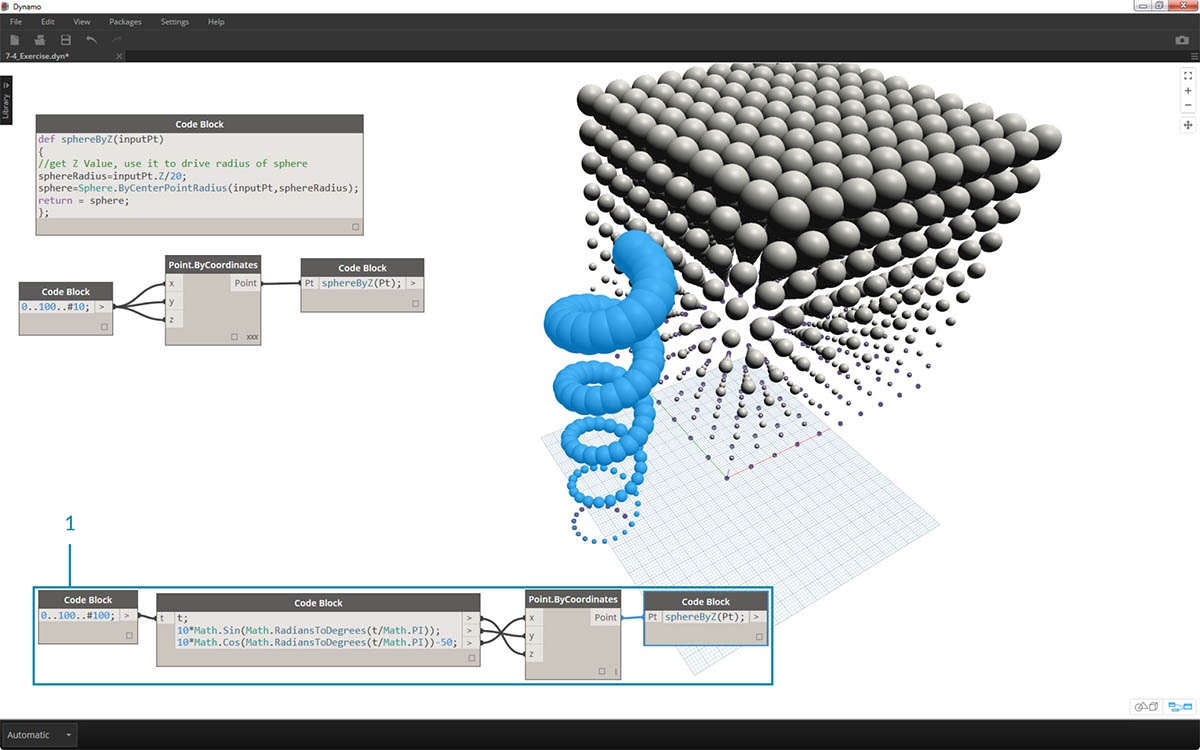
1. Pamiętaj, że utworzona przez nas funkcja sphereByZ to funkcja ogólna, więc możemy przywołać helisę z wcześniejszej lekcji i zastosować do niej tę funkcję.

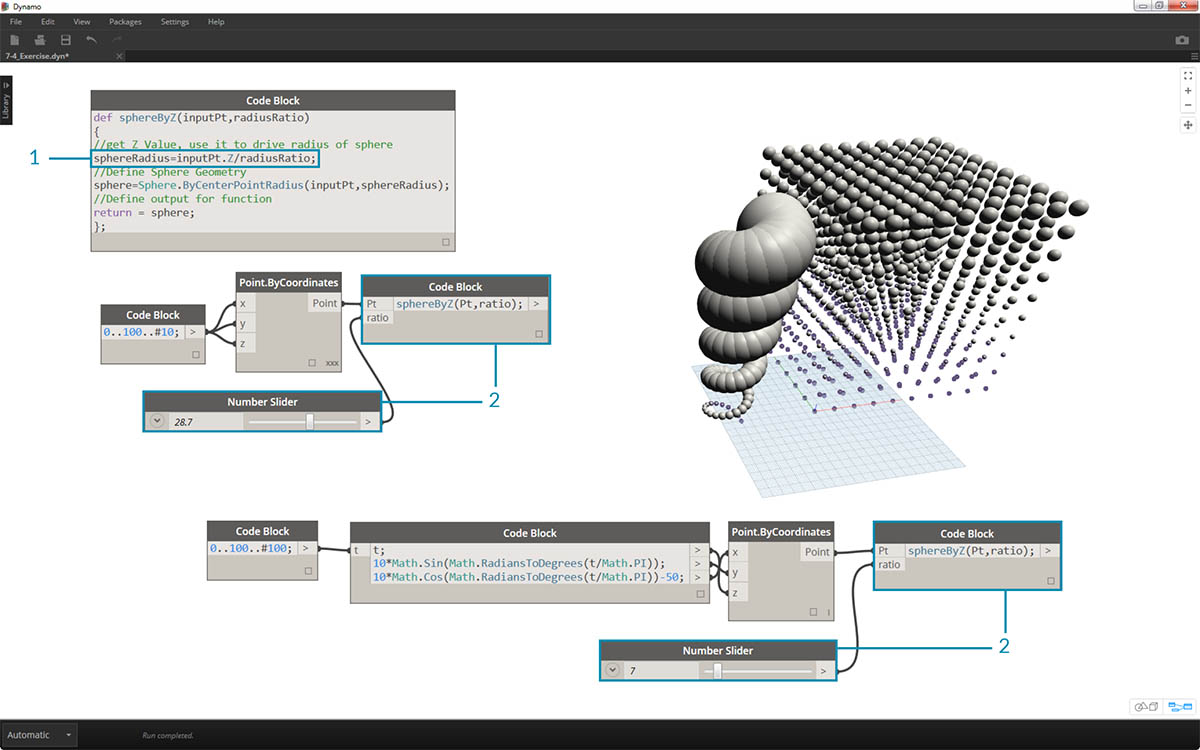
Ostatni krok: sterowanie współczynnikiem promienia za pomocą parametru zdefiniowanego przez użytkownika. Aby to zrobić, należy utworzyć nowe wejście dla tej funkcji, a także zastąpić dzielnik 20 parametrem.

1. Zaktualizuj definicję funkcji sphereByZ do postaci:

   def sphereByZ(inputPt,radiusRatio)
   {
   //get Z Value, use it to drive radius of sphere
   sphereRadius=inputPt.Z/radiusRatio;
   //Define Sphere Geometry
   sphere=Sphere.ByCenterPointRadius(inputPt,sphereRadius);
   //Define output for function
   return sphere;
   };
   

1. Zaktualizuj podrzędne bloki kodu, dodając do wejścia zmienną ratio: sphereByZ(Pt,ratio);. Podłącz suwak do nowo utworzonego wejścia bloku kodu i zmieniaj rozmiar promieni na podstawie współczynnika promienia.