Funkce bloku kódu

Funkce lze vytvořit v bloku kódu a lze je znovu načíst jinde v definici aplikace Dynamo. Tím se vytvoří další hladina ovládacího prvku v parametrickém souboru a lze ji zobrazit jako textovou verzi vlastního uzlu. V tomto případě je „nadřazený“ blok kódu snadno dostupný a může být umístěn kdekoli na grafu. Nepotřebuje žádné dráty!

Parent (Nadřazená jednotka)

První řádek obsahuje klíčové slovo „def“, pak název funkce a názvy vstupů v závorkách. Závorky definují tělo funkce. Vrátí hodnotu s „return =“. Uzly bloku kódu, které definují funkci, nemají vstupní nebo výstupní porty, protože se volají z jiných uzlů bloku kódu.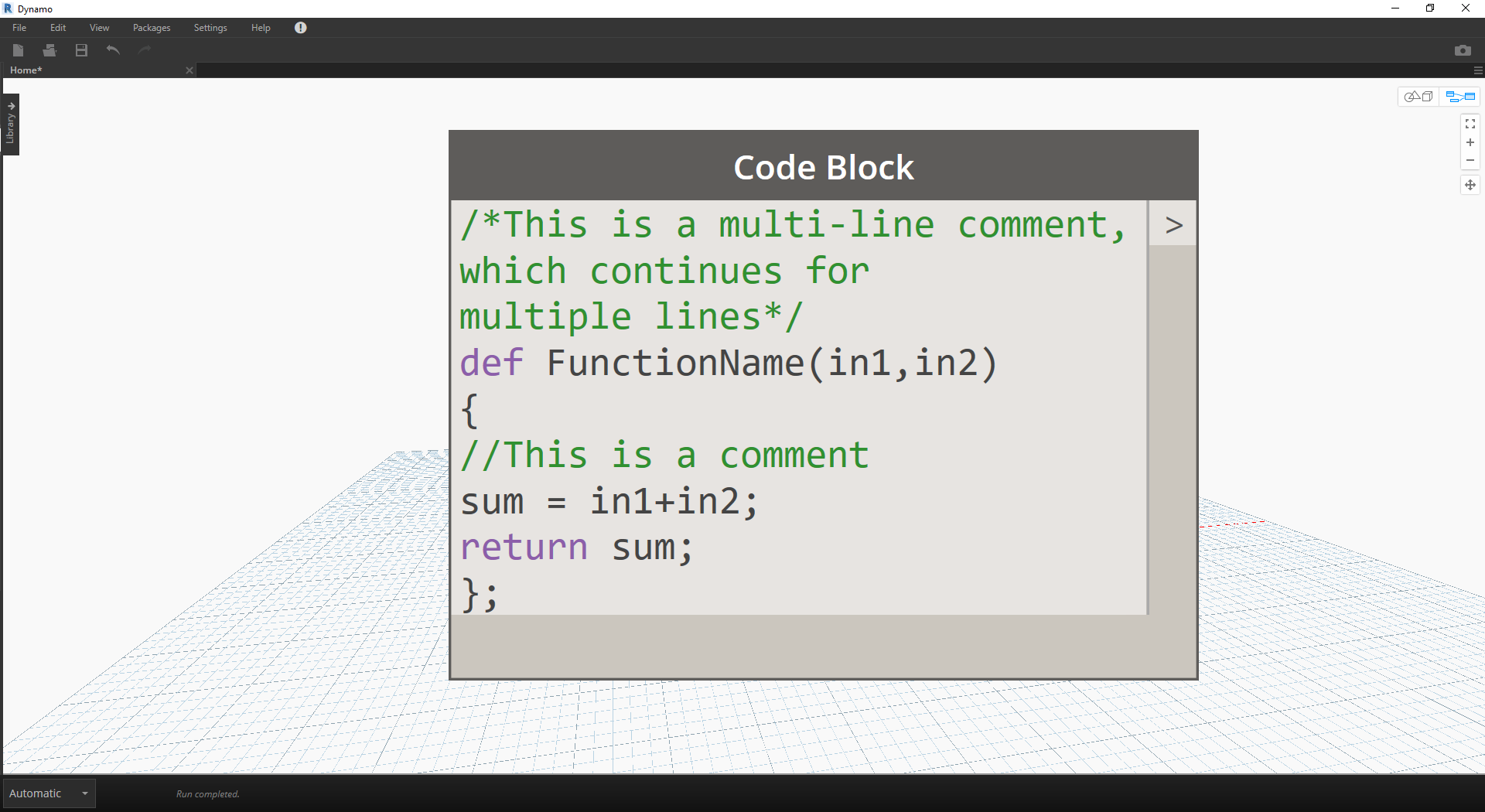

/*This is a multi-line comment,
which continues for
multiple lines*/
def FunctionName(in1,in2)
{
//This is a comment
sum = in1+in2;
return sum;
};

Podřazené položky

Volejte funkci s jiným uzlem bloku kódu ve stejném souboru, a to poskytnutím stejného názvu a stejného počtu argumentů. Funguje stejně uzly v knihovně.

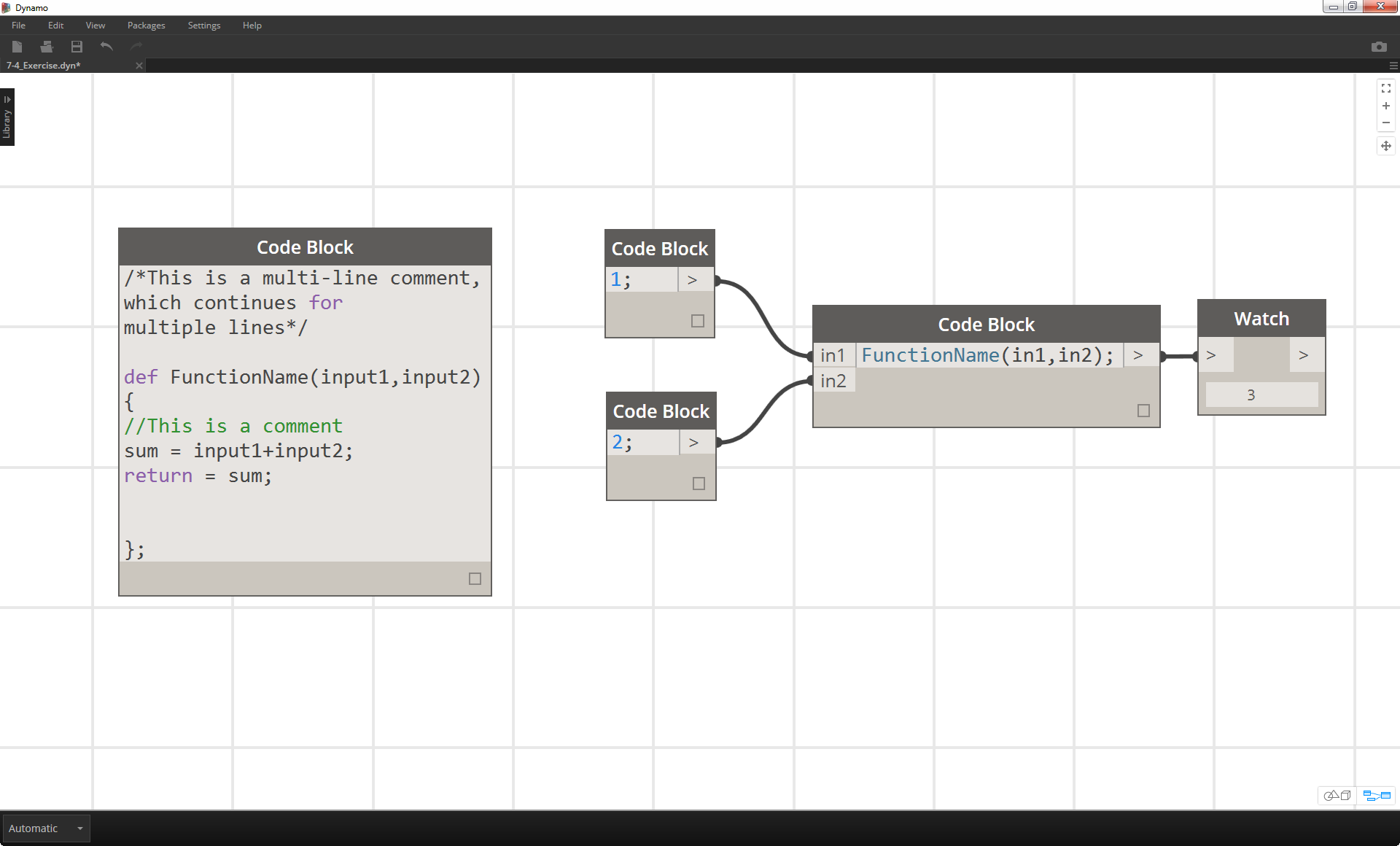
FunctionName(in1,in2);

Cvičení

Stáhněte si vzorový soubor, který je přiložen k tomuto cvičení (klikněte pravým tlačítkem a vyberte příkaz Uložit odkaz jako...). Úplný seznam vzorových souborů najdete v dodatku. Functions_SphereByZ.dyn

V tomto cvičení vytvoříme obecnou definici, která vytvoří koule ze vstupního seznamu bodů. Poloměr těchto koulí je řízen vlastností Z každého bodu.

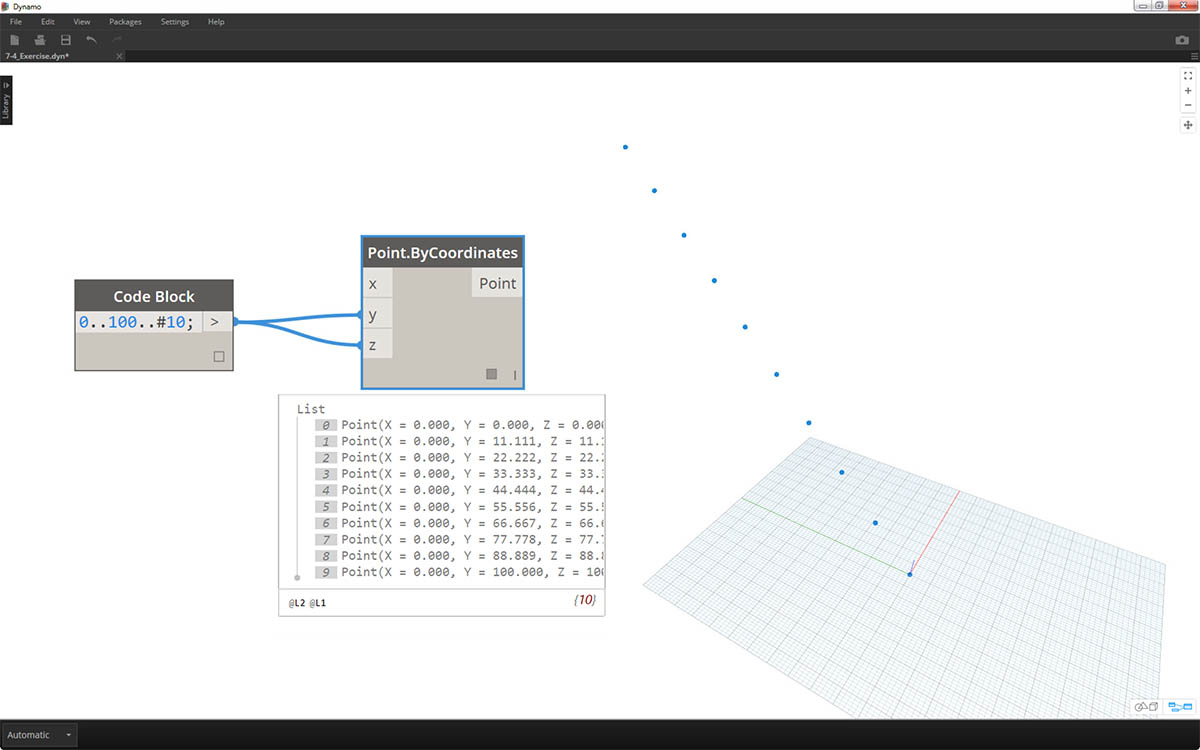
Začneme řadou deseti hodnot v rozsahu od 0 do 100. Tyto položky můžete vložit do uzlů Point.ByCoordinates za účelem vytvoření diagonální úsečky.

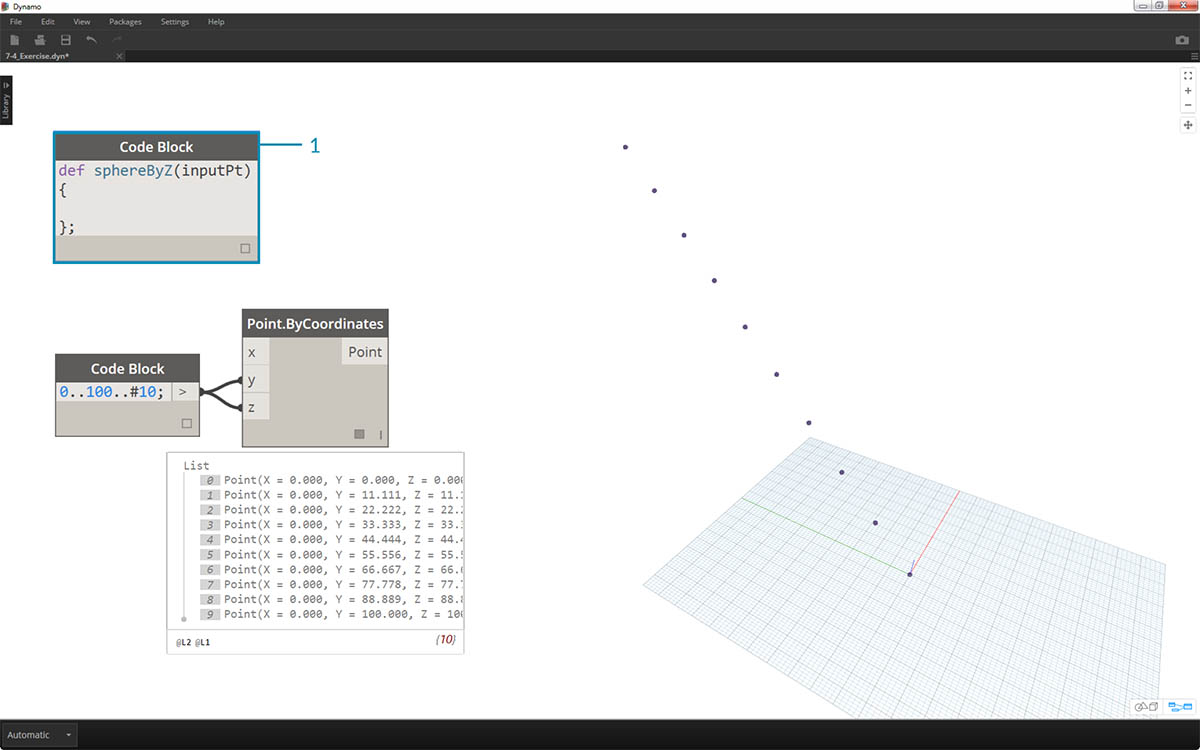
1. Vytvořte blok kódu a zaveďte naši definici pomocí řádku kódu:

   def sphereByZ(inputPt){
   };
   

InputPt je název, který jsme zadali k reprezentaci bodů, které budou řídit funkci. Zatím funkce nic nedělá, ale v následujících krocích ji rozšíříme.

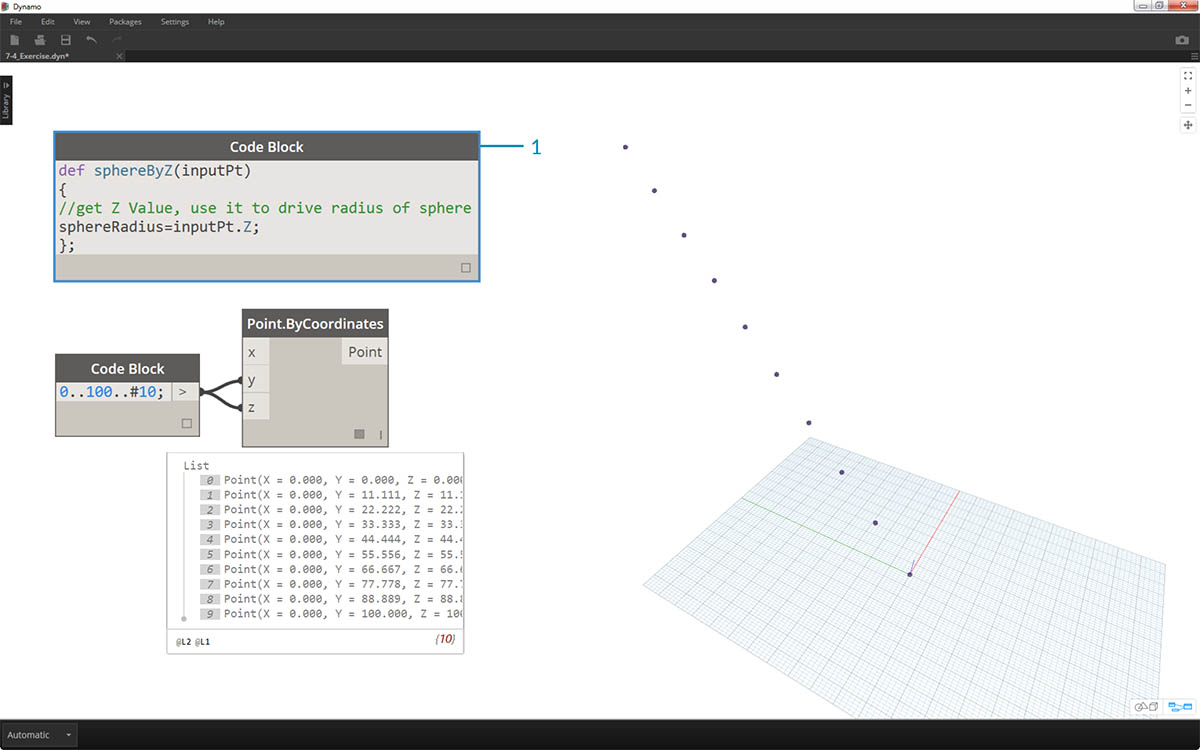
1. Přidáme-li funkci bloku kódu, umístíme komentář a proměnnou sphereRadius, která dotazuje pozici Z každého bodu. Nezapomeňte, že metoda inputPt.Z nevyžaduje jako metoda závorky. Toto je dotaz vlastností existujícího prvku, takže nejsou nutné žádné vstupy:

   def sphereByZ(inputPt,radiusRatio)
   {
   //get Z Value, use it to drive radius of sphere
   sphereRadius=inputPt.Z;
   };
   

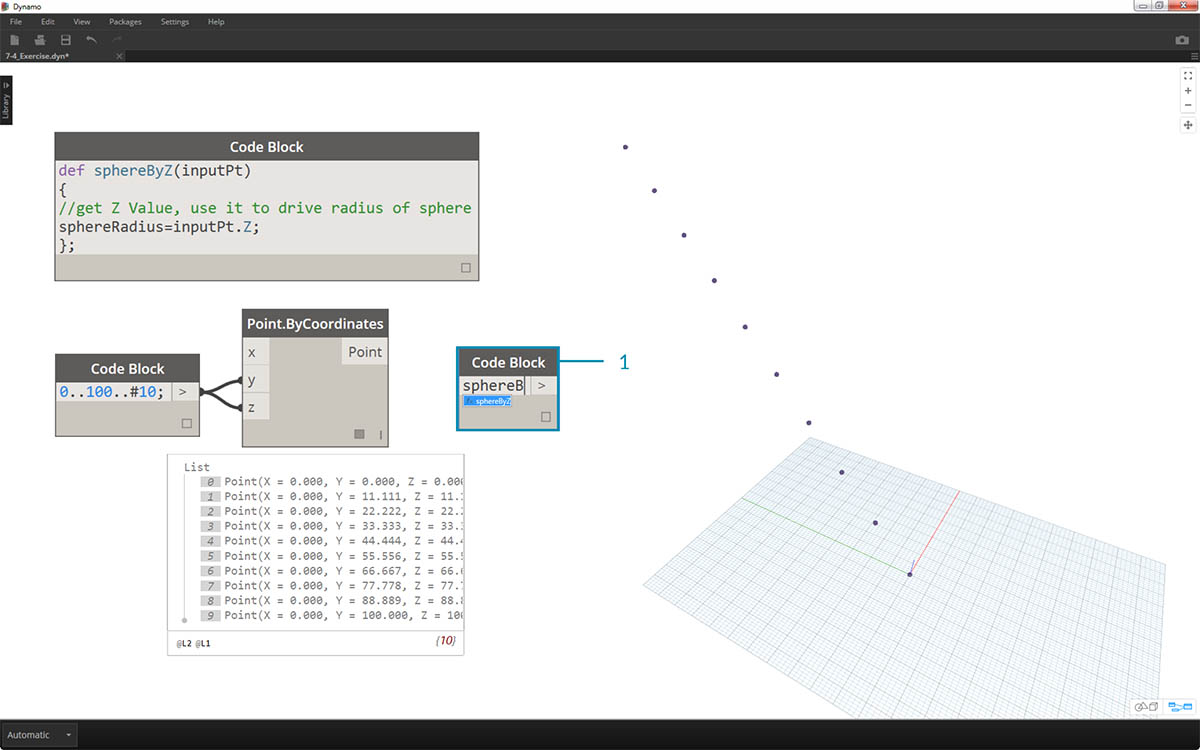
1. Nyní si připomeňme funkci, kterou jsme vytvořili v jiném bloku kódu. Pokud dvakrát klikneme na kreslicí plochu a vytvoříme nový blok kódu a zadáme jej do položky sphereB, všimneme si, že aplikace Dynamo navrhne funkci sphereByZ, kterou jsme definovali. Vaše funkce byla přidána do knihovny intellisense. Působivé.

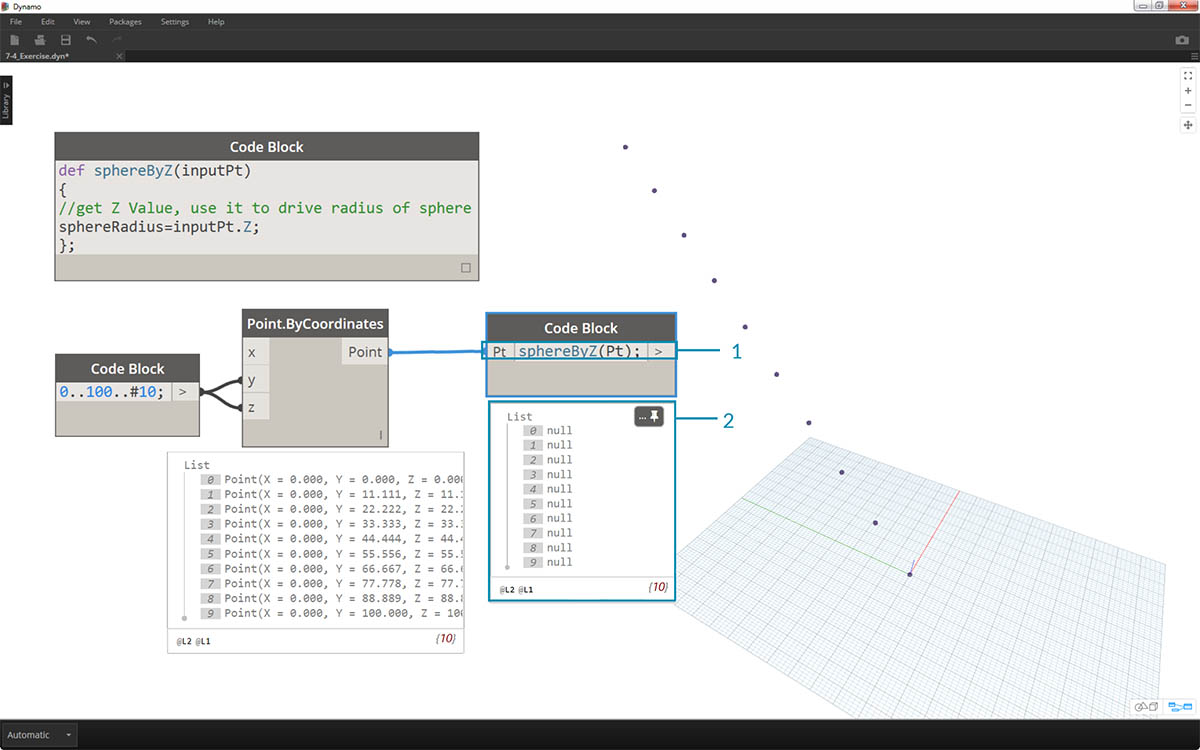
1. Nyní zavoláme funkci a vytvoříme proměnnou s názvem Pt, která bude zahrnovat body vytvořené v dřívějších krocích:

   sphereByZ(Pt)
   

1. Ve výstupu si všimneme, že máme všechny hodnoty null. Jak je to možné? Když jsme definovali funkci, vypočítali jsme proměnnou sphereRadius, ale nedefinovali jsme, co by měla funkce vrátit jako výstup. To můžeme opravit v dalším kroku.

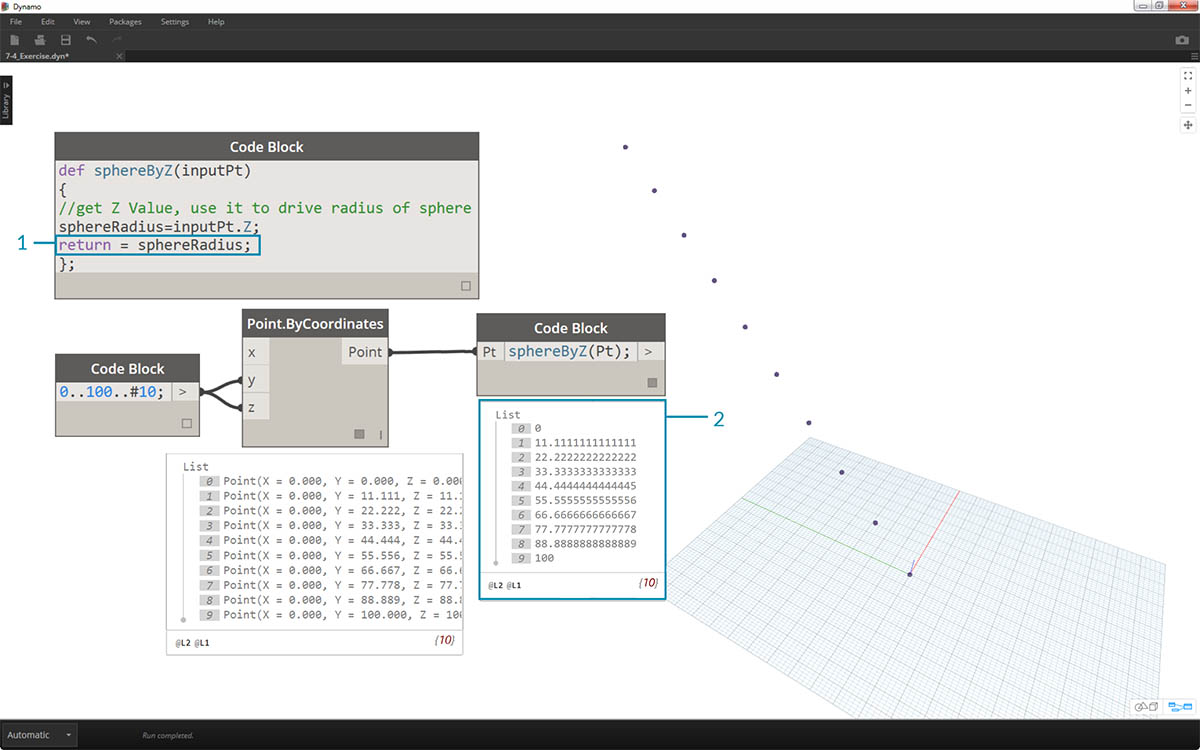
1. Důležitý krok je, abychom definovali výstup funkce přidáním řádku return = sphereRadius; do funkce sphereByZ.
2. Nyní vidíme, že výstupem bloku kódu jsou souřadnice Z každého bodu.

Nyní vytvoříme skutečné koule úpravou nadřazené funkce.

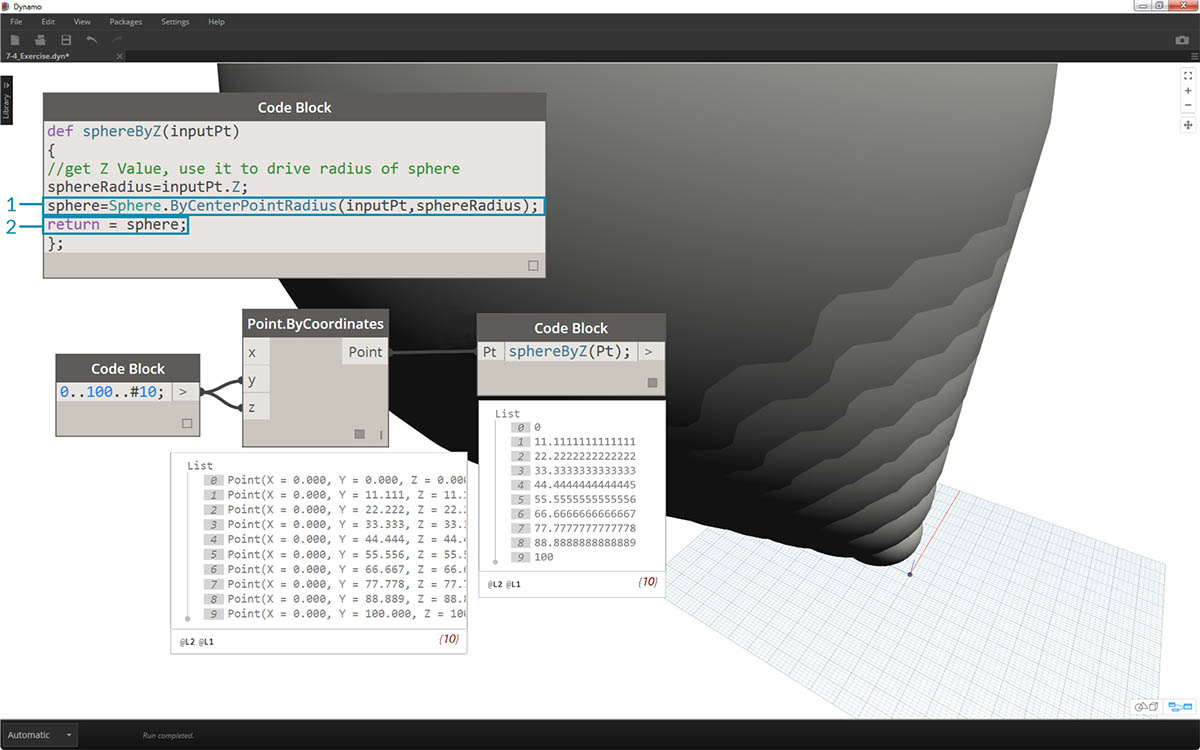
1. Nyní definujeme kouli řádkem kódu: sphere=Sphere.ByCenterPointRadius(inputPt,sphereRadius);
2. Dále změníme návratovou hodnotu na sphere místo sphereRadius: return = sphere;. Tak získáme obří koule v náhledu Dynamo.

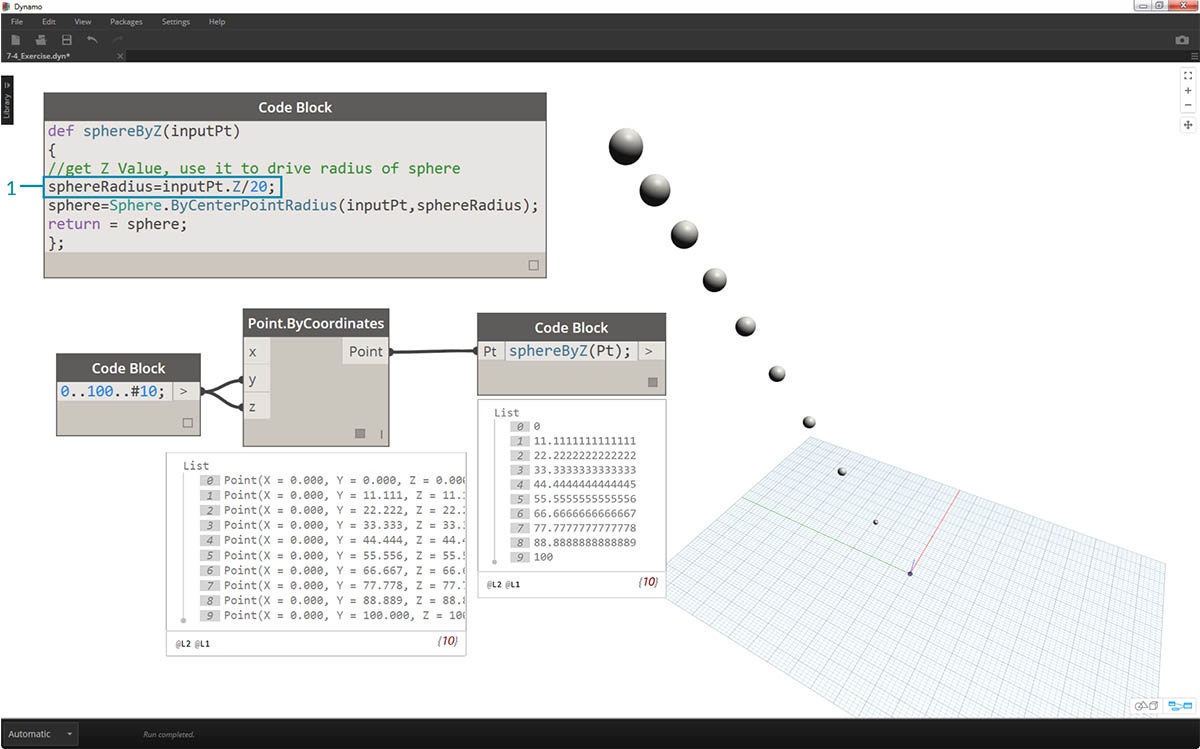
1. Chcete-li změnit velikost těchto koulí, aktualizujte hodnotu sphereRadius přidáním oddělovače: sphereRadius = inputPt.Z/20;. Nyní vidíme samostatné koule a začneme chápat vztah mezi poloměrem a hodnotou Z.

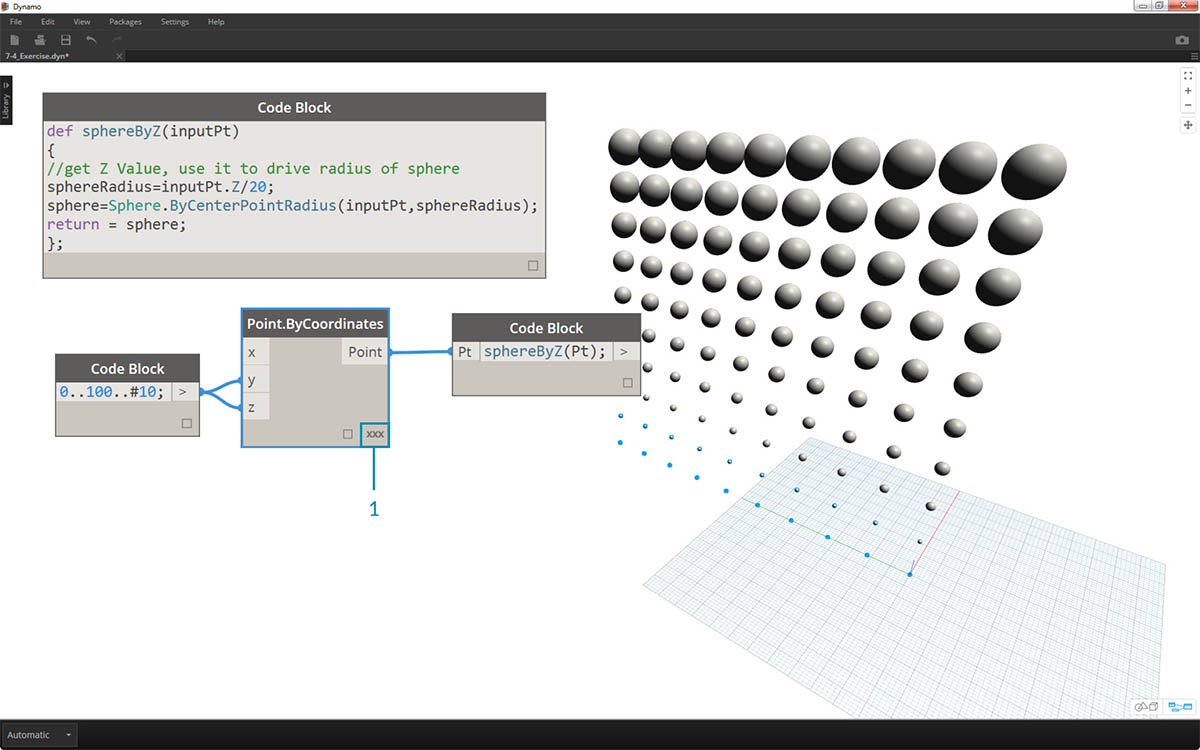
1. V uzlu Point.ByCoordinates změnou vázání z Nejkratší seznam na Kartézský součin vytvoříme rastr bodů. Funkce sphereByZ je stále plně funkční, takže všechny body vytvářejí koule s poloměry na základě hodnot Z.

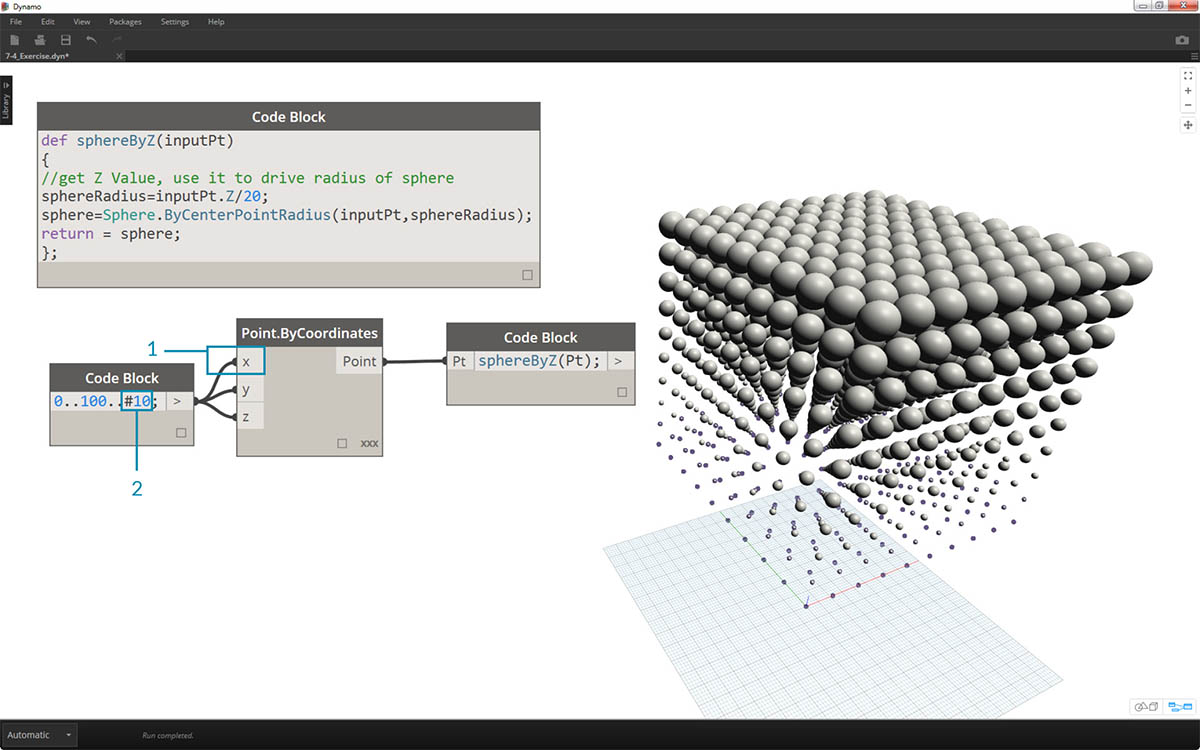
1. A jen tak na zkoušku připojíme původní seznam čísel do vstupu X uzlu Point.ByCoordinates. Teď máme krychli koulí.
2. Poznámka: Pokud výpočet trvá na vašem počítači dlouhou dobu, zkuste změnit číslo #10 na hodnotu #5.

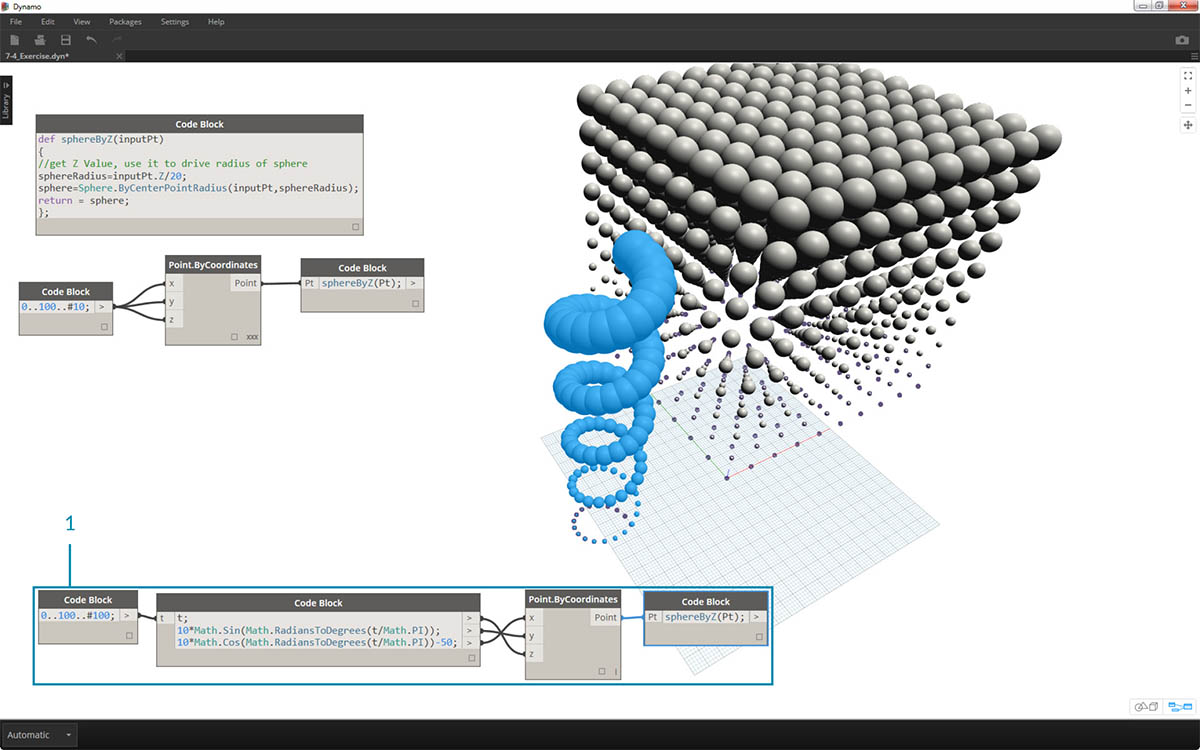
1. Pamatujte, že funkce sphereByZ, kterou jsme vytvořili, je obecná funkce, takže můžeme vyvolat šroubovici z předchozí lekce a použít na ni tuto funkci.

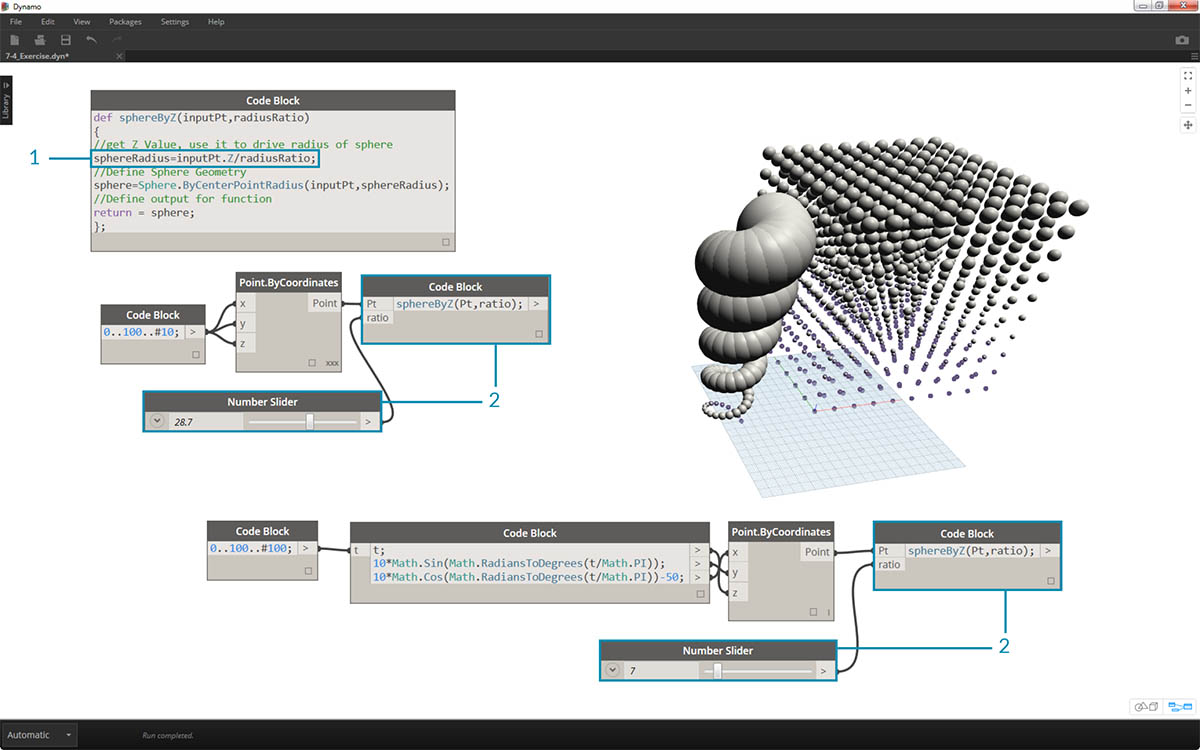
Jeden poslední krok: Pojďme řídit poměr poloměru s uživatelem definovaným parametrem. Chcete-li to udělat, je nutné vytvořit nový vstup pro funkci a také nahradit rozdělovač 20 parametrem.

1. Aktualizujte definici sphereByZ na:

   def sphereByZ(inputPt,radiusRatio)
   {
   //get Z Value, use it to drive radius of sphere
   sphereRadius=inputPt.Z/radiusRatio;
   //Define Sphere Geometry
   sphere=Sphere.ByCenterPointRadius(inputPt,sphereRadius);
   //Define output for function
   return sphere;
   };
   

1. Aktualizujte podřazené bloky kódu přidáním proměnné poměru ke vstupu: sphereByZ(Pt,ratio); Zapojte posuvník do nově vytvořeného vstupu bloku kódu a změňte velikost poloměrů podle poměru poloměrů.