Matematika
Pokud jsou nejjednodušší formou dat čísla, nejjednodušším způsobem, jak se tato čísla mohou odlišit, je použití funkce Mathematics. Od jednoduchých operátorů, jako je dělení, až k trigonometrickým funkcím, možnost Math je skvělým způsobem, jak začít zkoumat číselné vztahy a vzory.
Aritmetické operátory
Operátory jsou sada komponent, které používají algebraické funkce se dvěma číselnými vstupními hodnotami, které vrací jednu výstupní hodnotu (součet, rozdíl, násobení, dělení atd.). Najdete je pod položkou Operátory > Akce.
| Ikona | Název | Syntaxe | Vstupy | Výstupy |
|---|---|---|---|---|
| Součet | + | var[]...[], var[]...[] | var[]...[] | |
| Odčítání | - | var[]...[], var[]...[] | var[]...[] | |
| Násobení | * | var[]...[], var[]...[] | var[]...[] | |
| Dělení | / | var[]...[], var[]...[] | var[]...[] |
Parametrický vzorec
Stáhněte si vzorový soubor, který je přiložen k tomuto cvičení (klikněte pravým tlačítkem a vyberte příkaz Uložit odkaz jako...): Stavební bloky programů – Math.dyn. Úplný seznam vzorových souborů naleznete v dodatku.
Další logický krok spočívá v kombinování operátorů a proměnných, které vytvoří složitější vztah prostřednictvím vzorců. Vytvoříme vzorec, který lze ovládat vstupními parametry, jako jsou posuvníky.
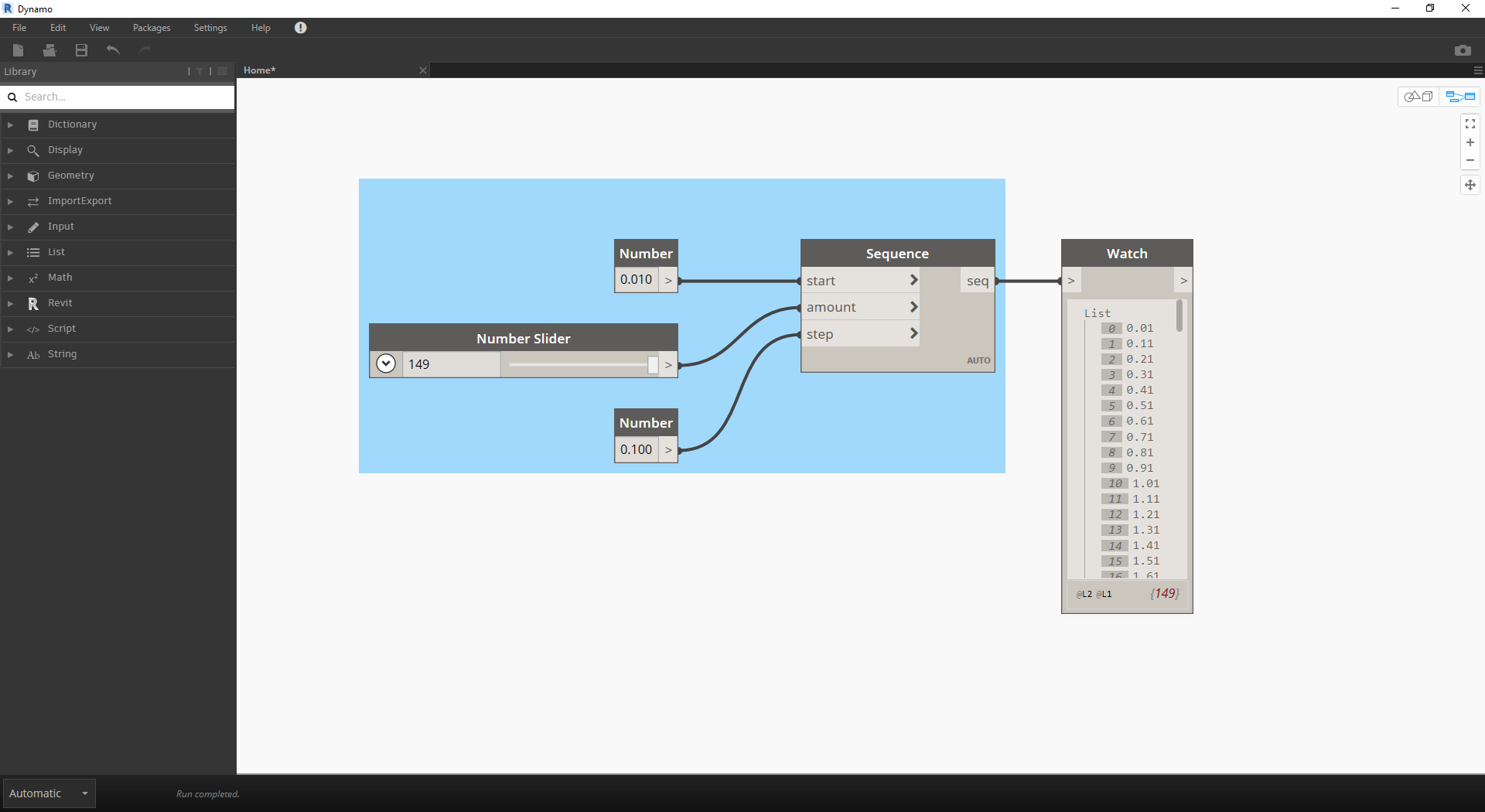
- Number Sequence: Definuje posloupnost čísel na základě tří vstupů: start, amount a step. Tato sekvence představuje „t“ v parametrické rovnici, takže chceme použít seznam, který je dostatečně velký k definici přechodnice.
Výše uvedený krok vytvořil seznam čísel definujících parametrickou doménu. Zlatá přechodnice je definována jako rovnice: 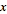 =
=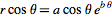 a
a 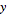 =
=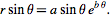 . Skupina uzlů níže představuje tuto rovnici ve vizuálním programovacím tvaru.
. Skupina uzlů níže představuje tuto rovnici ve vizuálním programovacím tvaru.
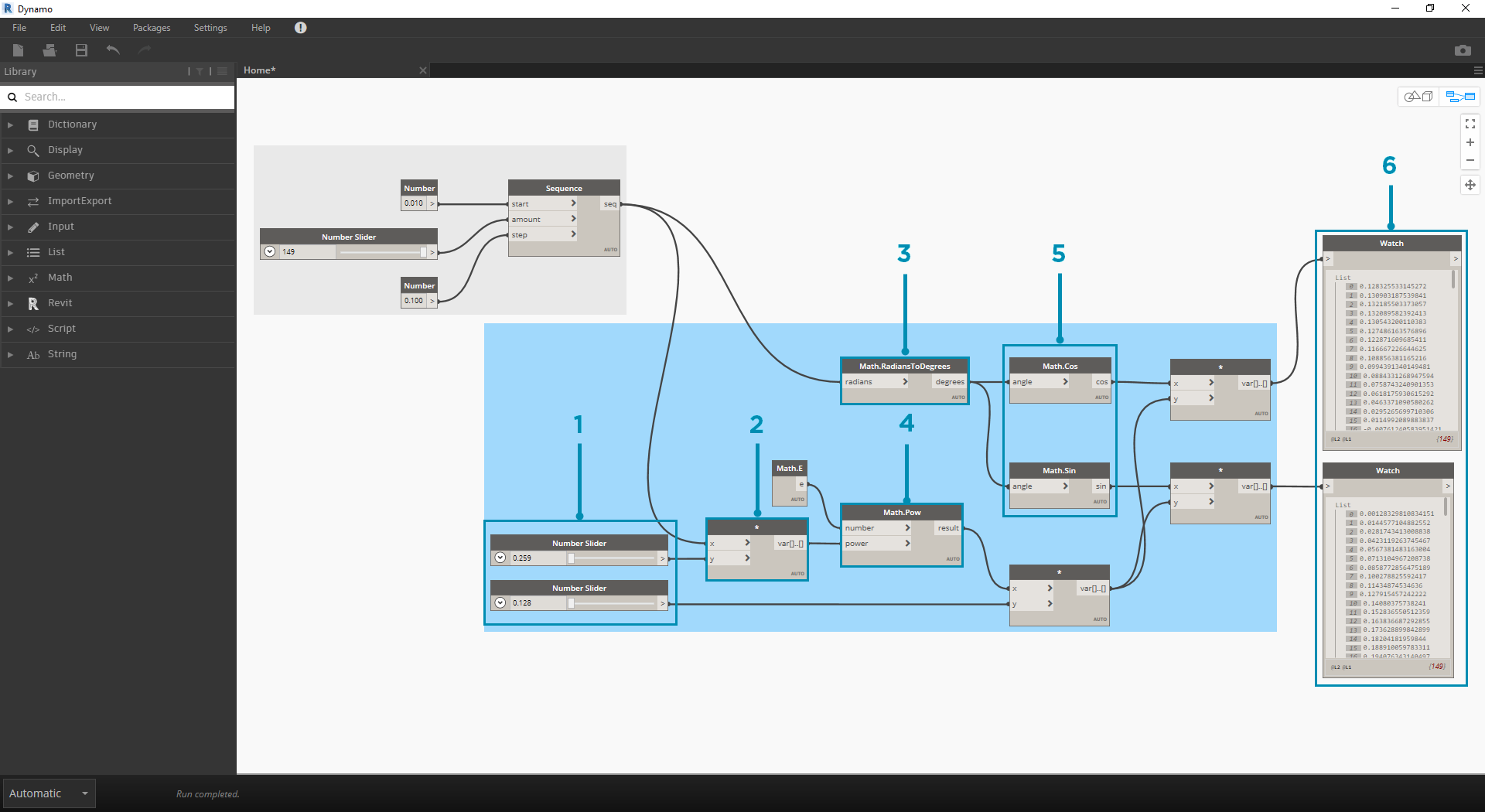
Při procházení skupiny uzlů se snažte věnovat pozornost souvislosti mezi vizuálním programem a psanou rovnicí.
- Number Slider: Přidejte na kreslicí plochu dva posuvníky. Tyto posuvníky budou představovat proměnné a a b parametrické rovnice. Představují konstantu, která je flexibilní, nebo parametry, které lze upravit podle požadovaného výsledku.
- * : uzel násobení je reprezentován hvězdičkou. Toto použijeme opakovaně k připojení násobných proměnných
- Math.RadiansToDegree: Hodnoty 't' je nutné převést na stupně pro jejich vyhodnocení v trigonometrických funkcích. Nezapomeňte, že aplikace Dynamo pro vyhodnocení těchto funkcí ve výchozím stavu používá stupně.
- Math.Pow: jako funkce 't' a čísla 'e' vytvoří sekvenci Fibonacci.
- Math.Cos a Math.Sin: Tyto dvě trigonometrické funkce odliší souřadnice X a souřadnice Y každého parametrického bodu.
- Watch: Nyní vidíte, že náš výstup jsou dva seznamy, které budou tvořit souřadnice x a y bodů použitých k vytvoření přechodnice.
Od vzorce ke geometrii
Nyní bude většina uzlů z předchozího kroku fungovat dobře, ale je to hodně práce. Chcete-li vytvořit efektivnější pracovní postup, podívejte se do části Bloky kódů (část 3.3.2.3) a definujte řetězec výrazů aplikace Dynamo do jednoho uzlu. V této další řadě kroků se podíváme na použití parametrické rovnice k nakreslení spirály Fibonacci. 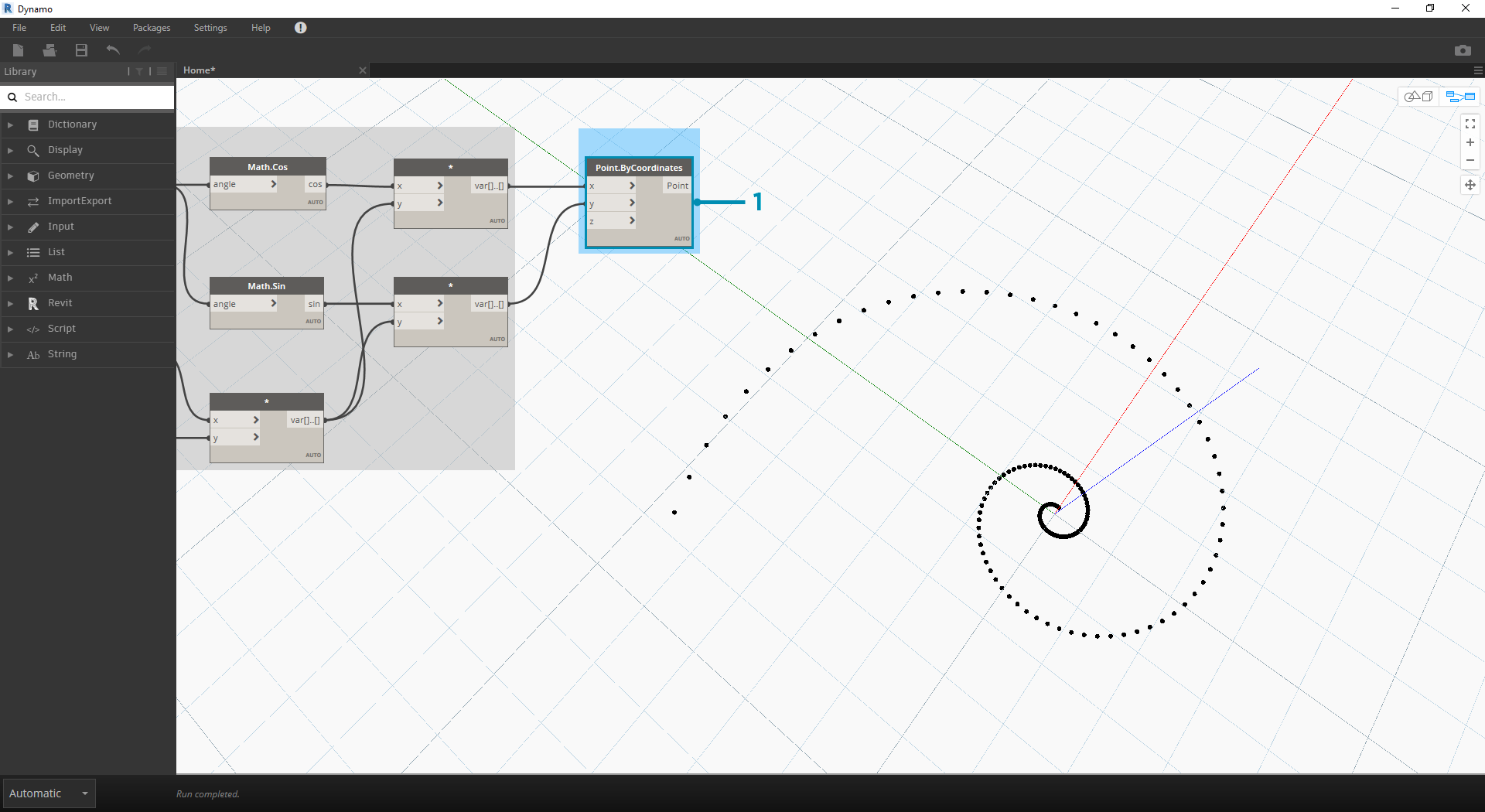
- Point.ByCoordinates: Spojte horní uzel násobení se vstupem x a dolní část se vstupem y. Nyní vidíte parametrickou spirálu bodů na obrazovce.
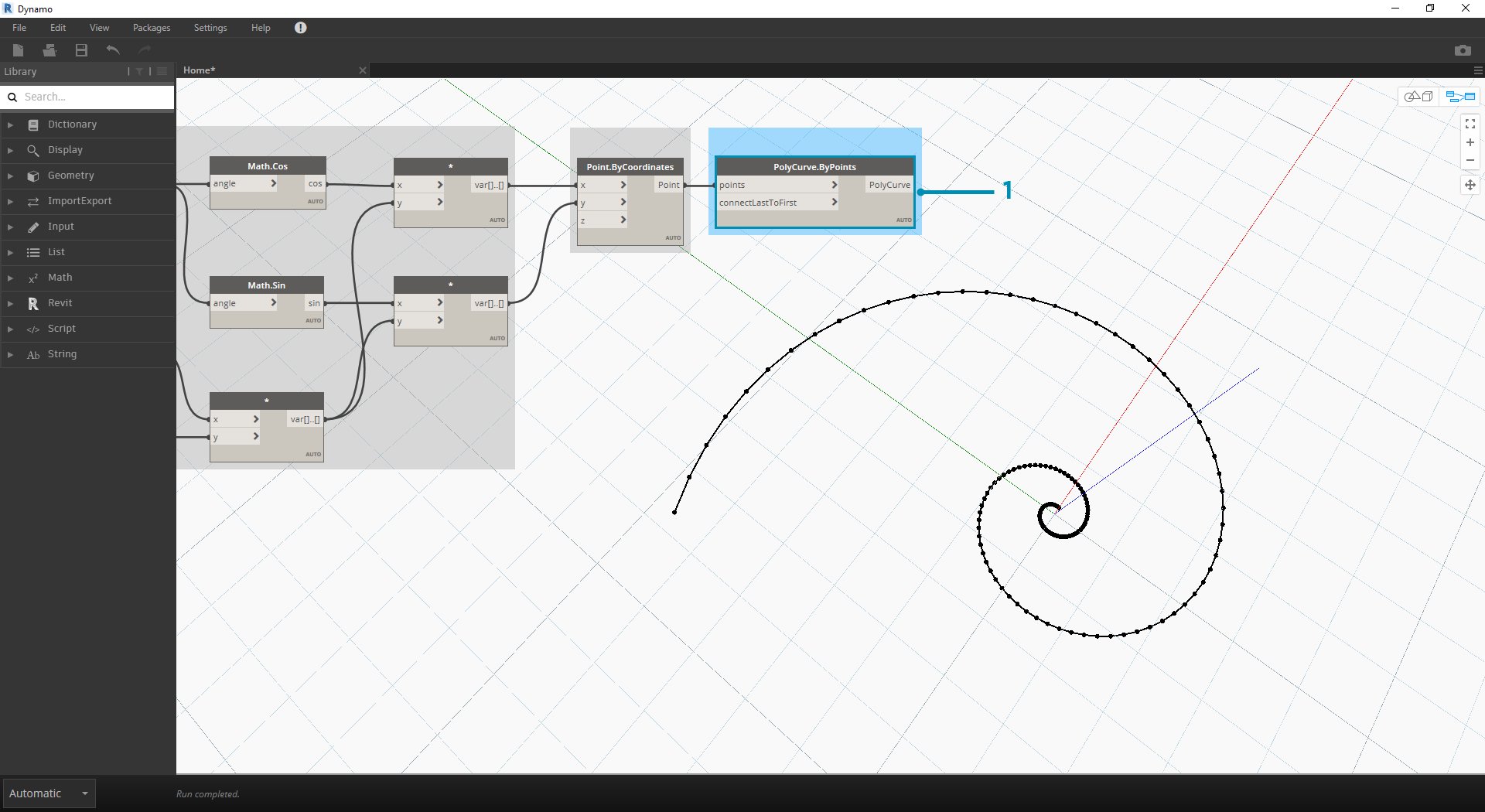
- Polycurve.ByPoints: Připojte soubor Point.ByCoordinates z předchozího kroku do bodů. Možnost connectLastToFirst můžeme nechat bez vstupu, protože neděláme uzavřený oblouk. Tím se vytvoří přechodnice, která prochází každým bodem definovaným v předchozím kroku.
Nyní jsme dokončili spirálu Fibonacci. Pojďme pokračovat ve dvou různých cvičeních, které pojmenujeme Nautilus a Sunflower. Jedná se o abstrakce přírodních systémů, ale dvě různá použití Fibonacciho spirály budou dobře zastoupena.
Od spirály k Nautilus

- Jako bod přesunu začneme stejným krokem z předchozího cvičení: Vytvoření spirálového pole bodů pomocí uzlu Point.ByCoordinates.
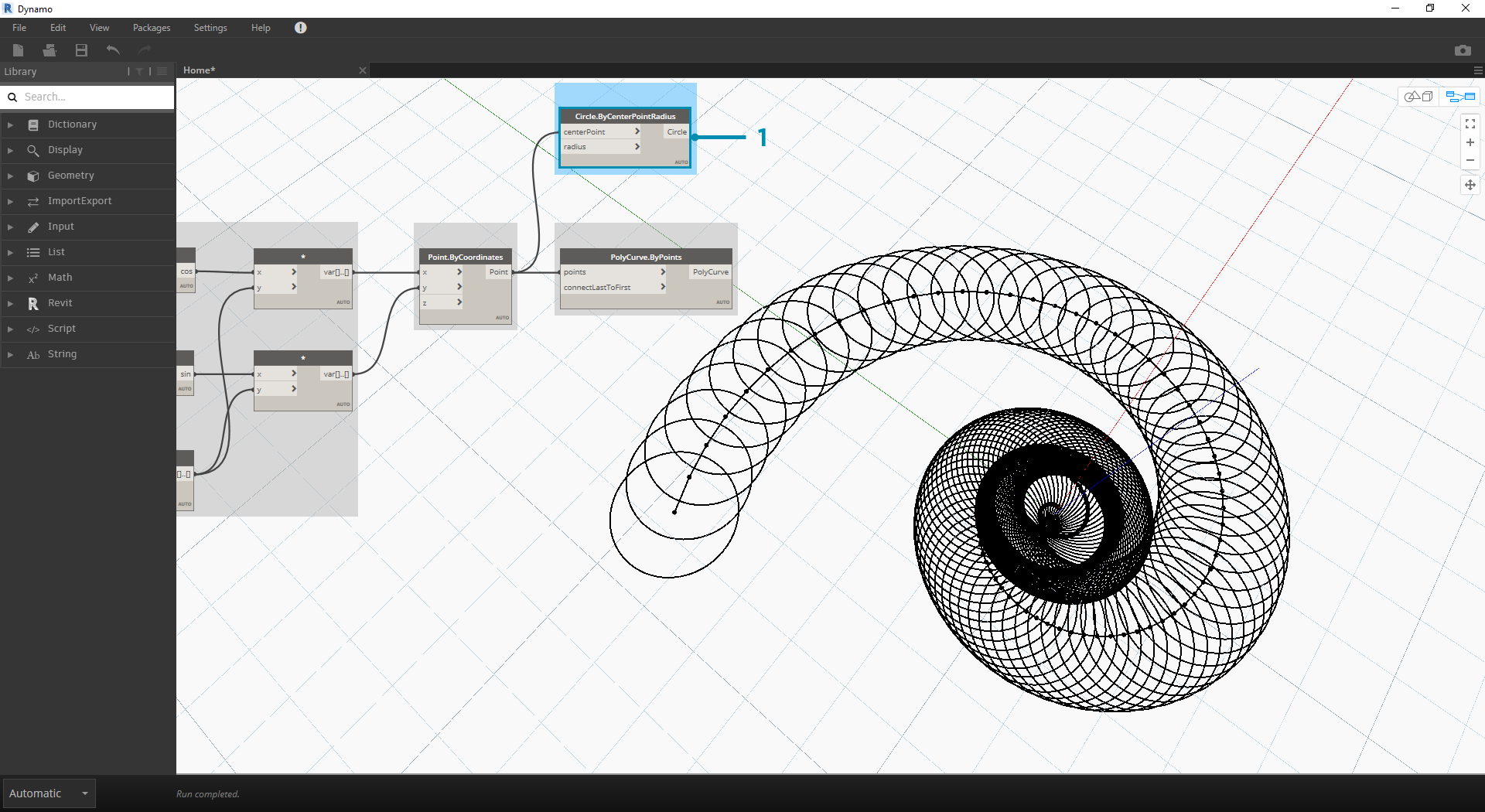
- Polycurve.ByPoints: Opět se jedná o uzel z předchozího cvičení, který použijeme jako referenci.
- Circle.ByCenterPointRadius: Zde použijeme kruhový uzel se stejnými vstupy jako v předchozím kroku. Výchozí hodnota poloměru je 1.0, takže je vidět okamžitý výstup kružnic. Je okamžitě čitelné, jak se body dále odchýlí od počátku.
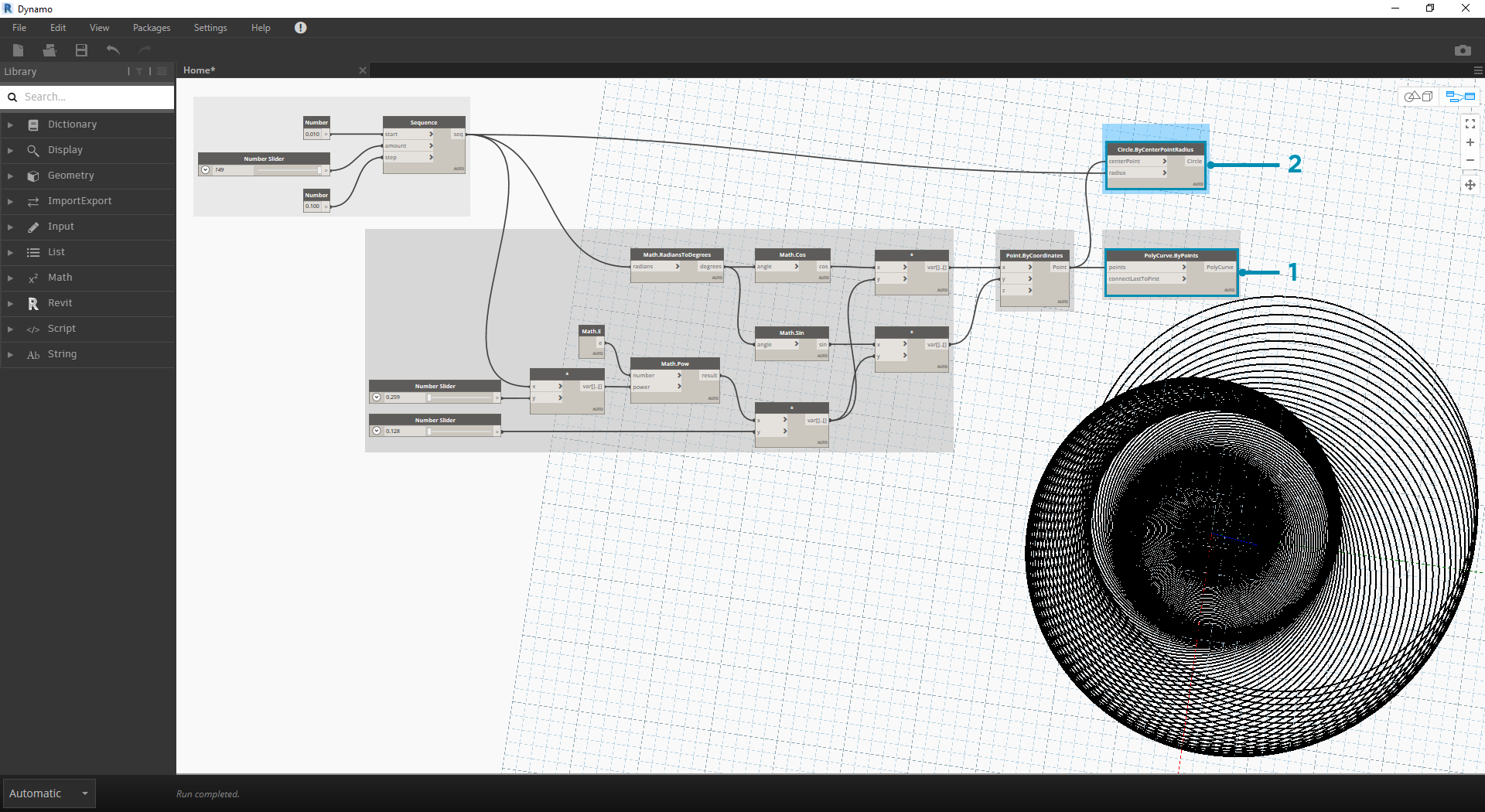
- Circle.ByCenterPointRadius: Pro vytvoření dynamičtějšího pole kružnic je nutné, aby původní číselná posloupnost (posloupnost 't') byla zadána do hodnoty poloměru.
- Number Sequence: Toto je původní pole 't'. Přidáním této hodnoty do poloměru se středy kružnic stále od počátku liší, ale poloměr kružnic se zvětšuje a vytváří Fibonacciho kruhový graf. Bonusové body, pokud to vytvoříte ve 3D.
Od Nautilus k Phyllotaxis Pattern
Teď, když jsme udělali kruhovou skořepinu Nautilus, pojďme skočit do parametrických rastrů. Použijeme základní otočení Fibonacciho spirály k vytvoření Fibonacciho rastru a výsledek bude modelován po růstu slunečnicových semen.

- Jako bod přesunu začneme znovu stejným krokem z předchozího cvičení: Vytvoření spirálového pole bodů pomocí uzlu Point.ByCoordinates.
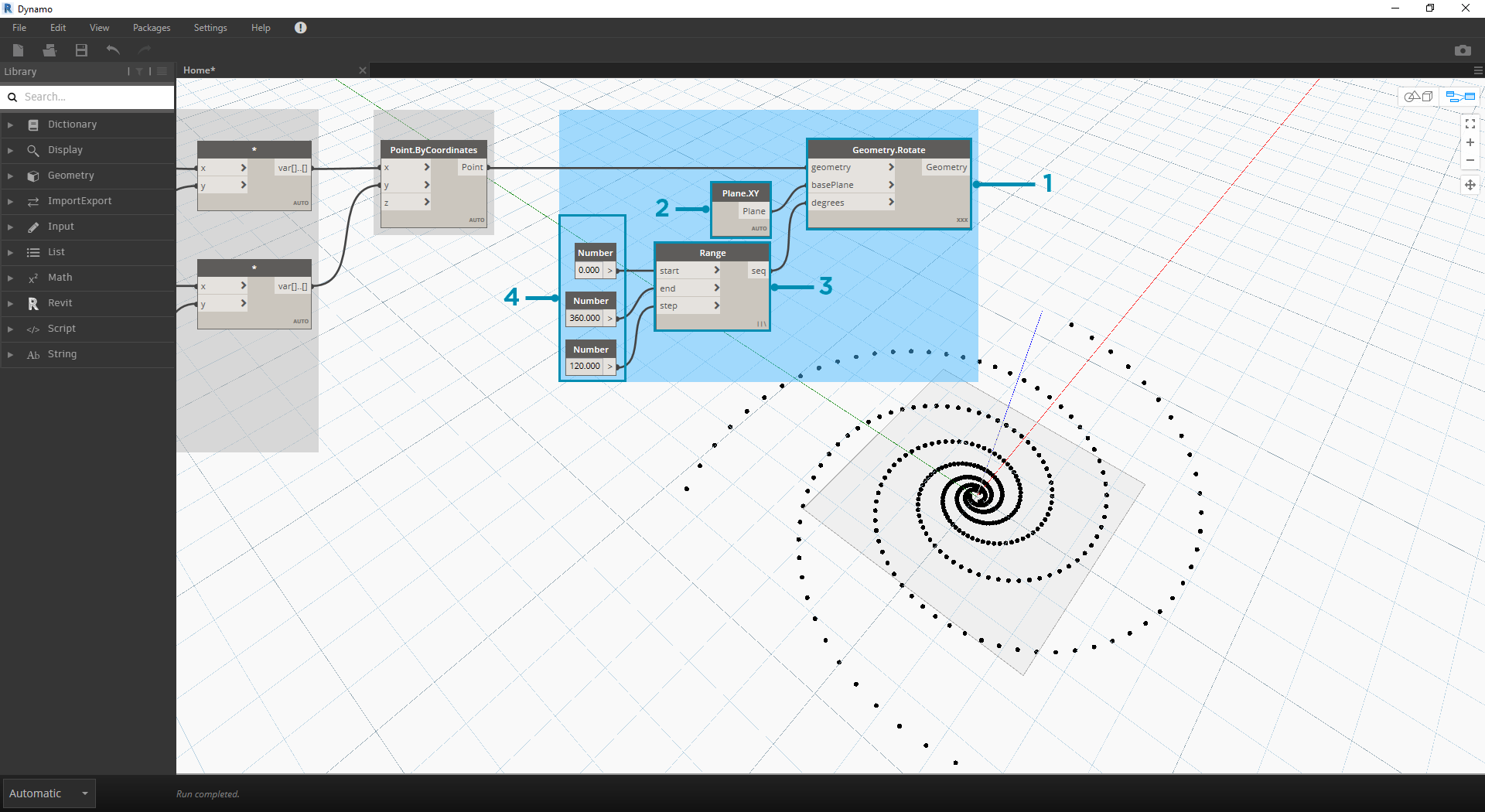
- Geometry.Rotate: Existuje několik možností Geometry.Rotate. Ujistěte se, že jste vybrali uzel se vstupy geometry,basePlane a degrees. Připojte položku Point.ByCoordinates ke vstupu geometrie.
- Plane.XY: Připojte se ke vstupu basePlane. Otočíme se kolem počátku, což je stejné umístění jako základna přechodnice.
- Number Range: Pro náš vstup stupně chceme vytvořit více otočení. To můžeme provést rychle pomocí komponenty Number Range. Připojte jej ke vstupu degrees.
- Number: A k definování rozsahu čísel přidejte na kreslicí plochu ve vertikálním pořadí tři uzly čísel. Shora dolů přiřaďte hodnoty 0.0,360.0 a 120.0 v uvedeném pořadí. Toto jsou řídicí otáčení přechodnice. Po připojení tří uzlů čísel k uzlu si všimněte výstupních výsledků z uzlu Number Range.
Náš výstup se začíná podobat víru. Upravíme některé parametry položky Number Range a podíváme se, jak se výsledky mění: 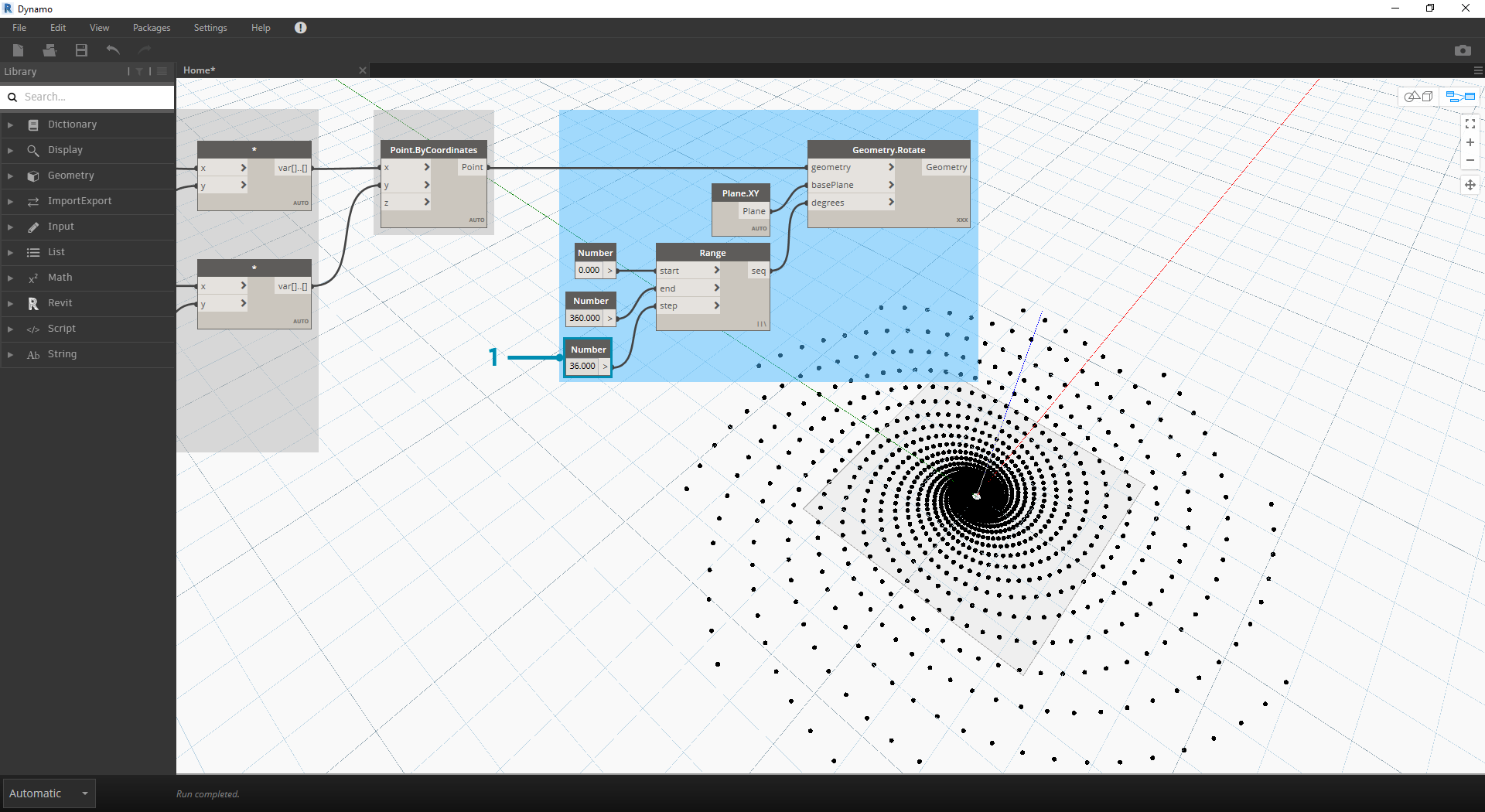
- Změňte velikost kroku uzlu Number Range z 120.0 na 36.0. Všimněte si, že tím vznikají další otáčení, a proto získáváme hustý rastr.
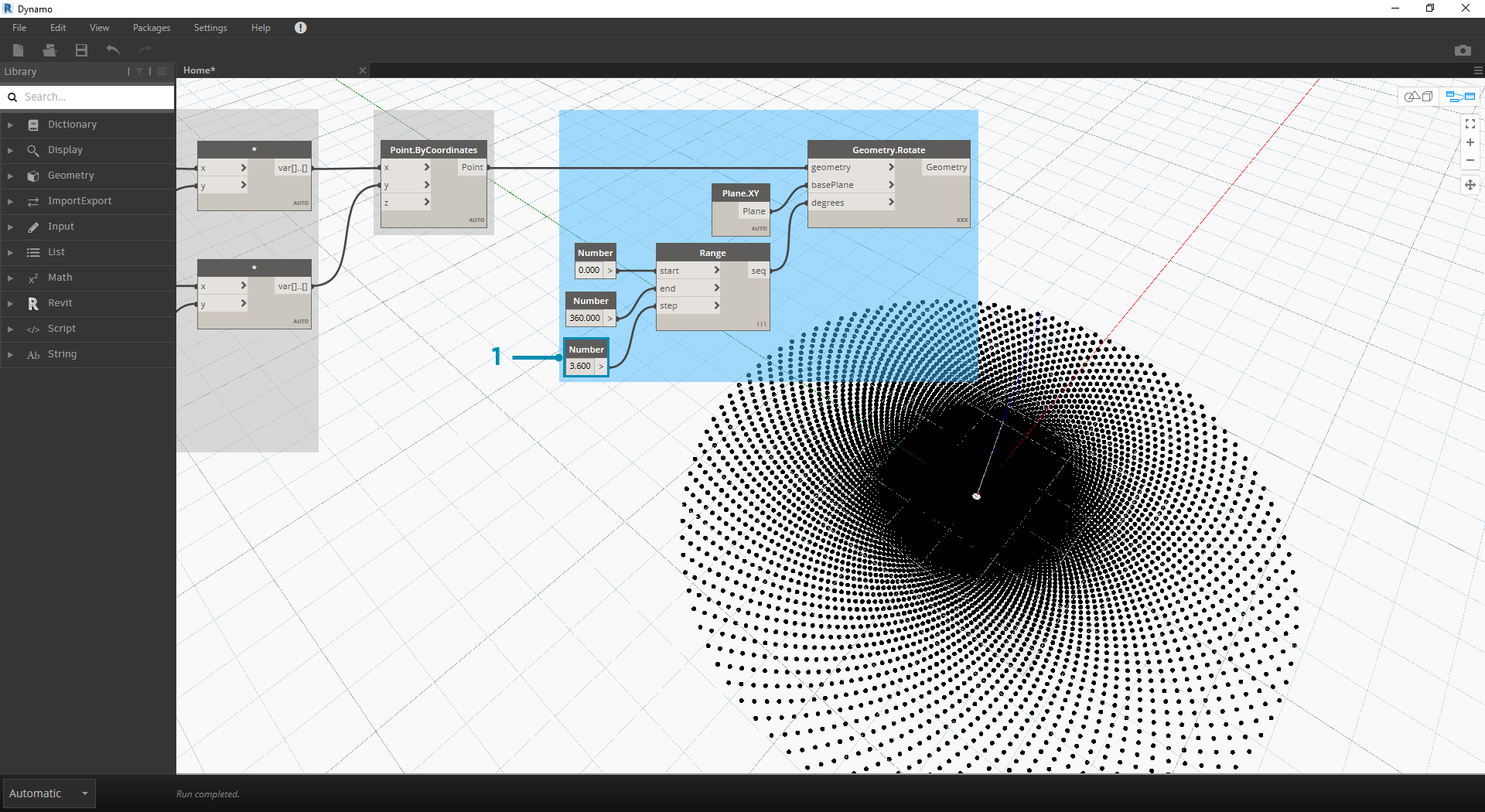
- Změňte velikost kroku uzlu Number Range z 36.0 na 3.6. To nám nyní dává mnohem hustější rastr a směr přechodnice není jasný. Dámy a pánové, vytvořili jsme slunečnici.