수학

가장 간단한 데이터 형식이 숫자인 경우 해당 숫자를 연결하는 가장 쉬운 방법은 수학을 사용하는 것입니다. 나누기와 같은 단순한 연산자부터 삼각 함수, 좀 더 복잡한 수식까지, 수학은 수치 관계 및 패턴을 탐색하기 위한 좋은 방법입니다.

산술 연산자

연산자는 두 개의 숫자 입력 값과 대수 함수를 사용하는 구성요소의 집합으로, 하나의 출력 값을 생성합니다(추가, 빼기, 곱하기, 나누기 등). 이러한 항목은 연산자>작업에서 찾을 수 있습니다.

아이콘	이름	구문	입력	출력
	추가	+	var[]...[], var[]...[]	var[]...[]
	빼기	-	var[]...[], var[]...[]	var[]...[]
	곱하기	*	var[]...[], var[]...[]	var[]...[]
	나누기	/	var[]...[], var[]...[]	var[]...[]

파라메트릭 수식

이 연습과 함께 제공되는 예시 파일(프로그램의 빌딩 블록 - Math.dyn)을 다운로드하십시오(마우스 오른쪽 버튼을 클릭하고 "다른 이름으로 링크 저장..." 선택). 전체 예시 파일 리스트는 부록에서 확인할 수 있습니다.

연산자에서 다음 논리적 단계는 연산자와 변수를 결합하여 수식을 통해 보다 복잡한 관계를 형성하는 것입니다. 슬라이더와 같이 입력 매개변수로 제어할 수 있는 수식을 만들어 보겠습니다.

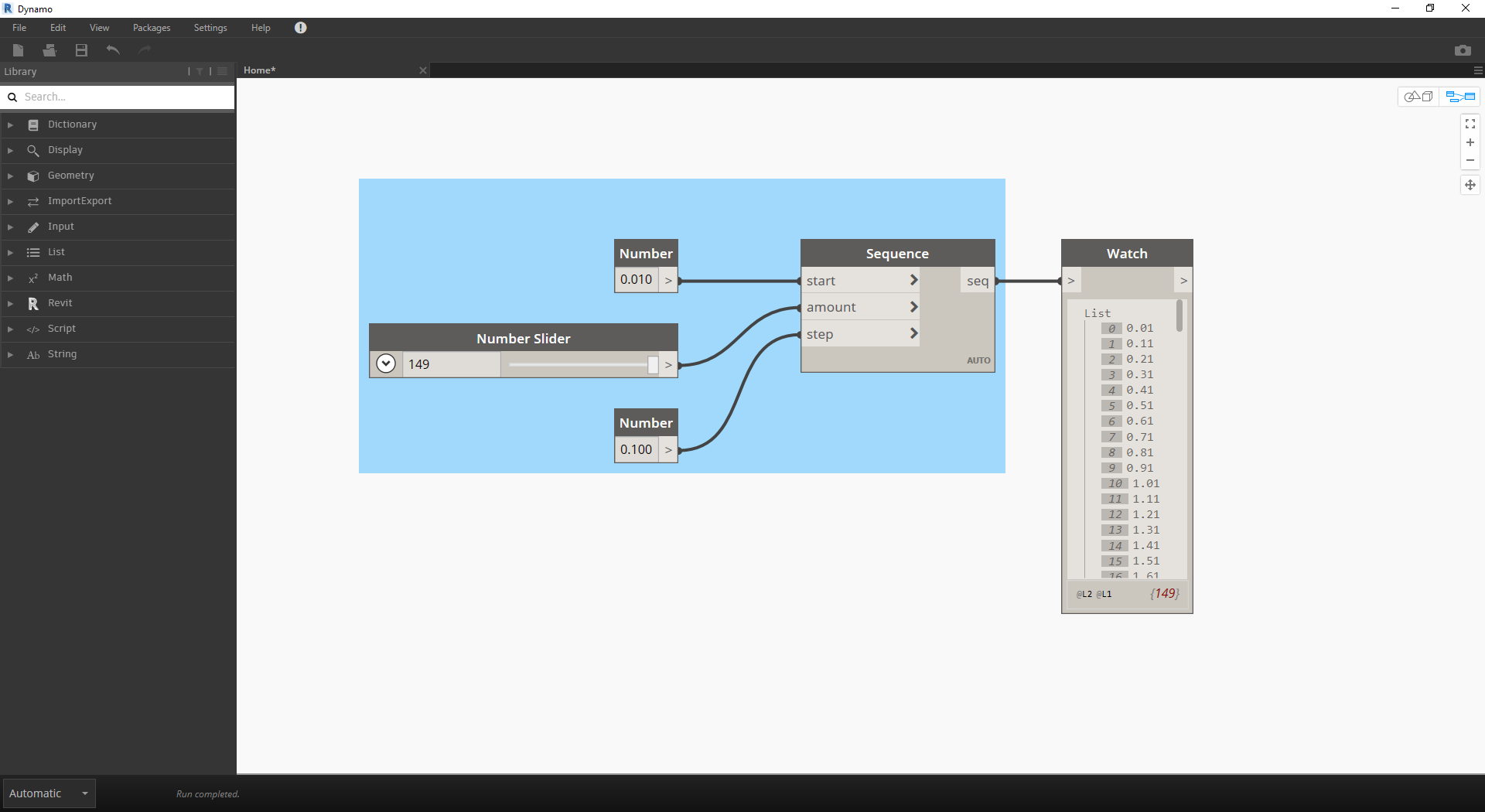
1. Number Sequence: start, amount 및 step의 세 가지 입력에 따라 숫자 시퀀스를 정의합니다. 이 시퀀스는 파라메트릭 방정식에서 't'를 나타내므로 나선을 정의할 수 있을 만큼 충분히 큰 리스트를 사용하려고 합니다.

위의 단계에서는 파라메트릭 도메인을 정의하는 숫자 리스트를 작성했습니다. 황금 나선은 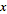= 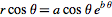및 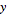= 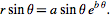방정식으로 정의됩니다. 아래의 노드 그룹은 이 방정식을 시각적 프로그래밍 양식으로 나타냅니다.

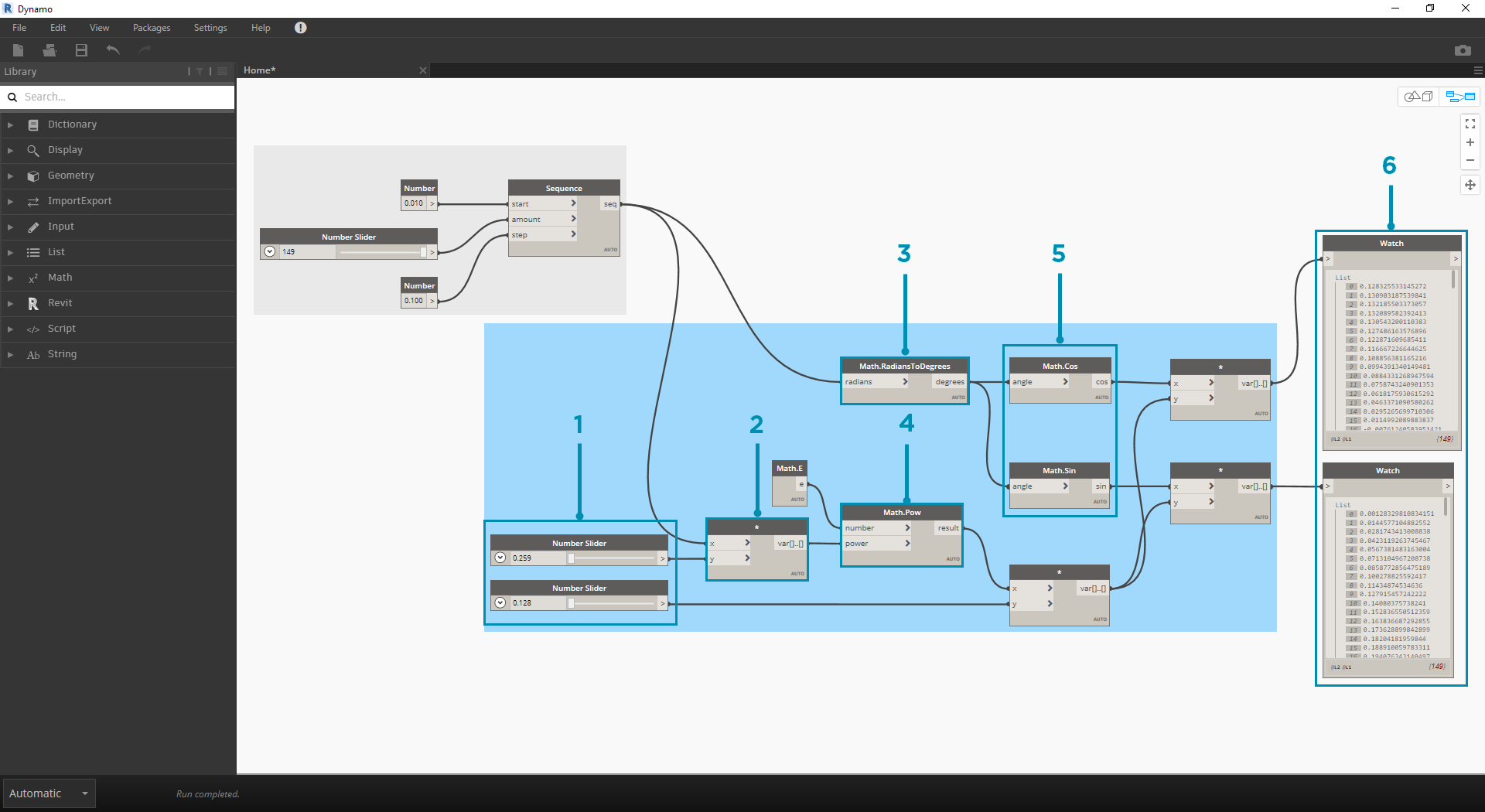
노드 그룹을 단계별로 진행하면서 시각적 프로그램과 작성된 방정식 간의 평행에 주의를 기울이십시오.

1. Number Slider: 캔버스에 2개의 숫자 슬라이더를 추가합니다. 이러한 슬라이더는 파라메트릭 방정식의 a 및 b 변수를 나타냅니다. 이러한 슬라이더는 유동적인 상수 또는 원하는 결과를 얻기 위해 조정할 수 있는 매개변수를 나타냅니다.
2. * : 곱하기 노드는 별표로 표시됩니다. 이를 반복적으로 사용하여 곱하기 변수를 연결하겠습니다.
3. Math.RadiansToDegrees: 삼각 함수에서 평가하기 위해 't' 값을 각도로 변환해야 합니다. Dynamo에서는 이러한 함수를 평가하기 위해 기본적으로 각도로 설정됩니다.
4. Math.Pow: 't' 및 숫자 'e'의 함수로, Fibonacci 시퀀스를 작성합니다.
5. Math.Cos 및 Math.Sin: 이러한 두 삼각 함수는 각 파라메트릭 점의 x 좌표와 y 좌표를 각각 구분합니다.
6. Watch: 이제 출력이 두 개의 리스트로 표시됩니다. 이러한 출력은 나선을 생성하는 데 사용되는 점의 x 및 y 좌표가 됩니다.

수식을 형상으로

이제 이전 단계의 대량 노드는 제대로 작동하지만 여기에는 상당히 많은 작업이 필요합니다. 보다 효율적인 워크플로우를 작성하려면 Code Block(섹션 3.3.2.3)을 살펴보고 Dynamo 표현식의 문자열을 하나의 노드로 정의하십시오. 이 다음 단계 시리즈에서는 파라메트릭 방정식을 사용하여 Fibonacci 나선을 그리는 방법을 살펴보겠습니다.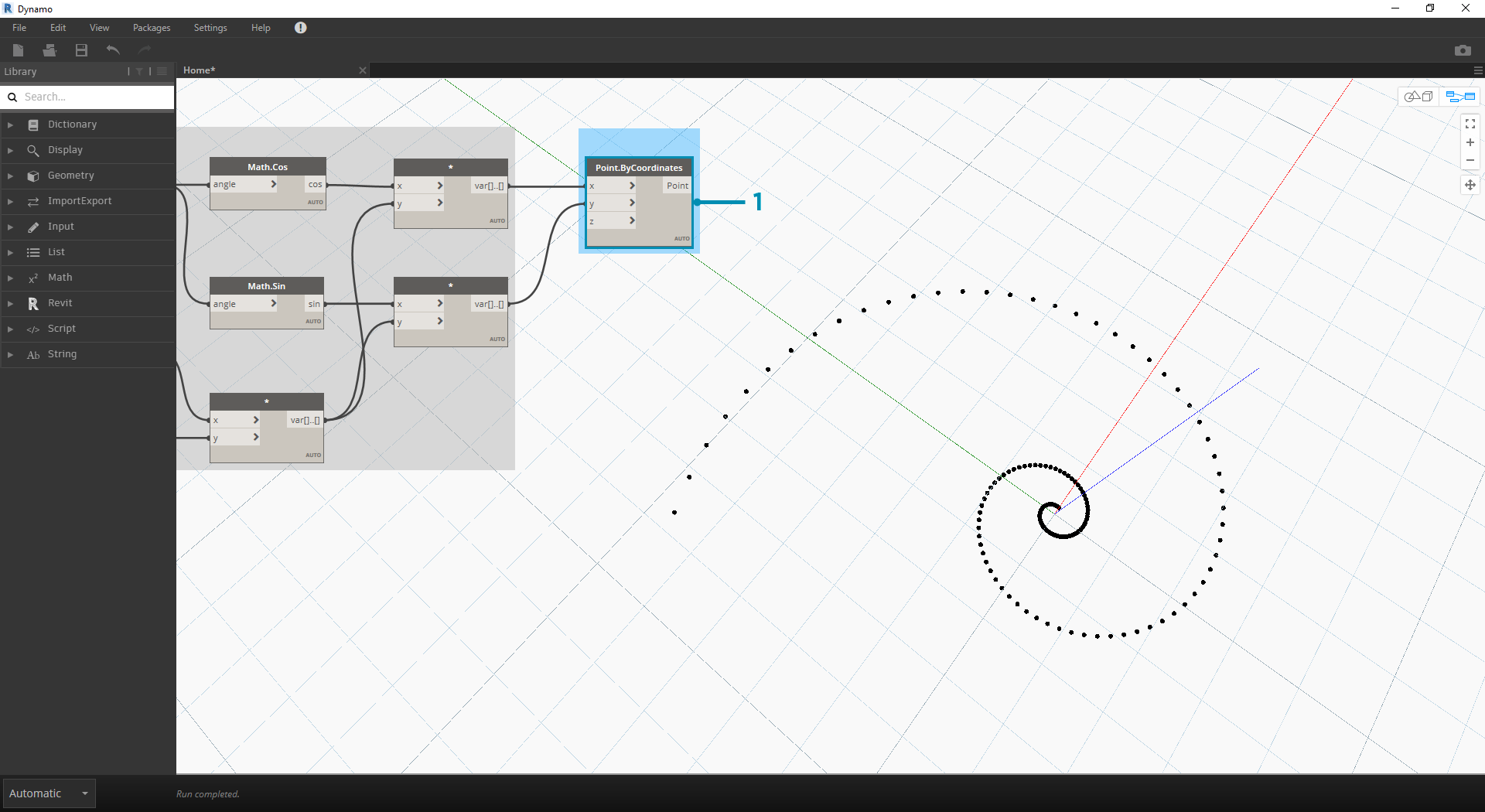

1. Point.ByCoordinates: 상단의 곱하기 노드를 'x' 입력에 연결하고 하단의 노드를 'y' 입력에 연결합니다. 이제 화면에 파라메트릭 나선형 점이 표시됩니다.

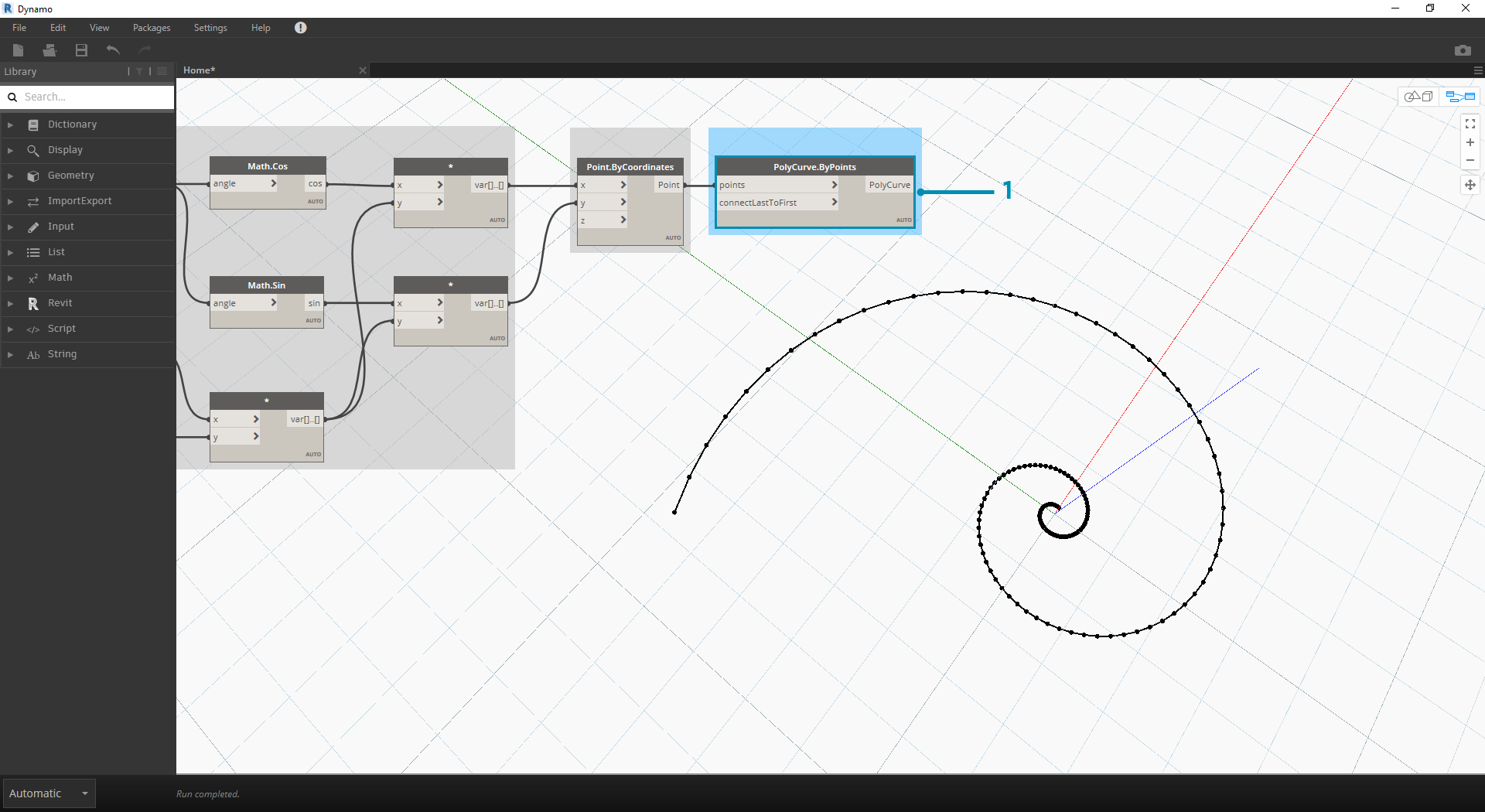
1. Polycurve.ByPoints: 이전 단계의 Point.ByCoordinates를 points에 연결합니다. 닫힌 곡선을 만드는 것이 아니므로 입력 없이 connectLastToFirst를 그대로 두면 됩니다. 그러면 이전 단계에서 정의한 각 점을 통과하는 나선이 작성됩니다.

이제 Fibonacci 나선을 완료했습니다. 여기에서 두 가지 개별 연습을 추가로 진행하여 Nautilus와 Sunflower를 호출해 보겠습니다. 이 둘은 자연 시스템을 추상적으로 나타낸 것이지만, Fibonacci 나선의 두 가지 다른 응용을 잘 보여 줍니다.

나선을 Nautilus로

1. 이전 연습의 동일한 단계인 Point.ByCoordinates 노드로 나선형 점 배열 작성하기부터 시작해 보겠습니다.

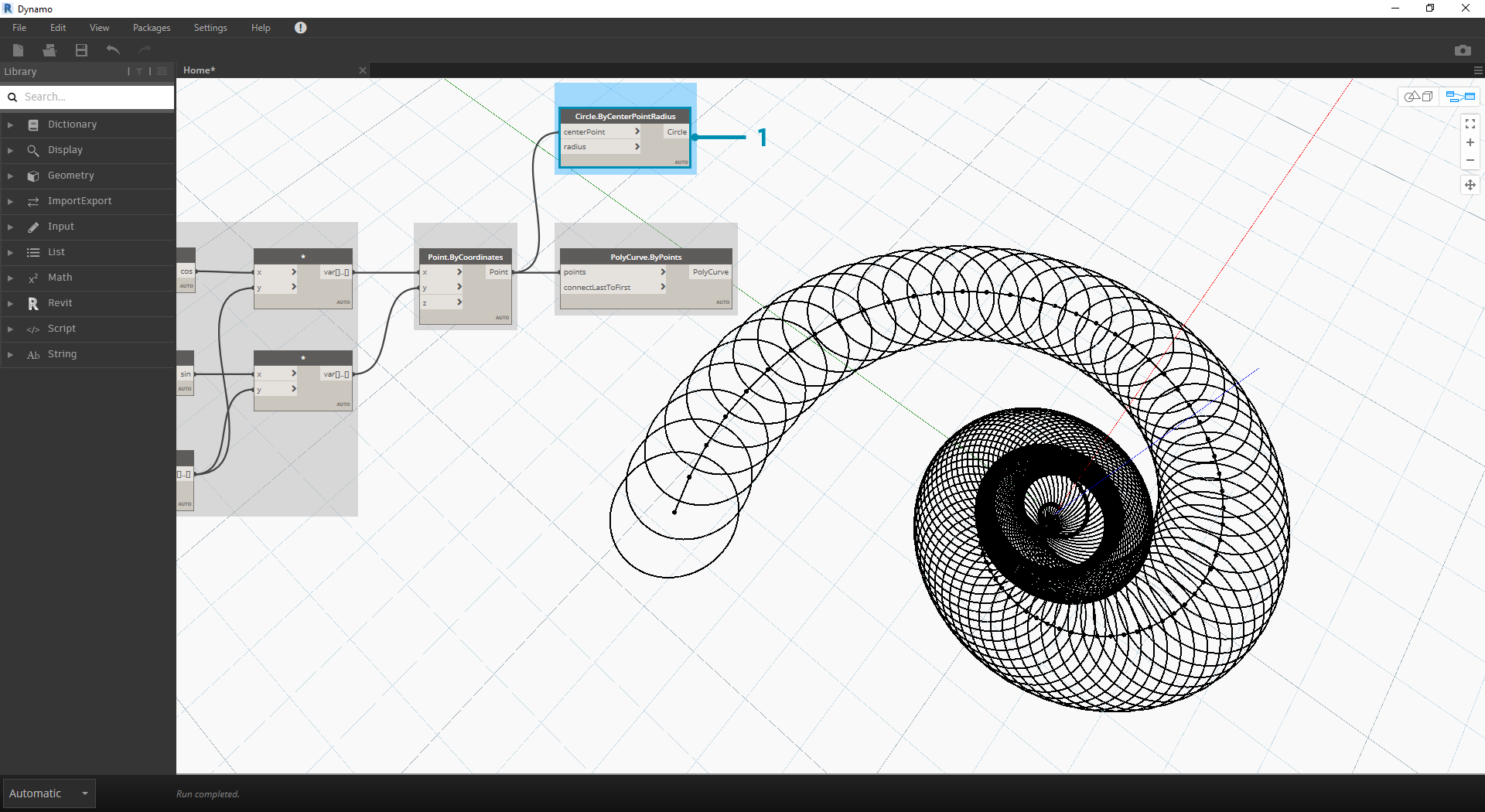
1. Polycurve.ByPoints: 다시 한번 말씀드리자면 이는 이전 연습에서 사용한 노드이며 참조로 사용할 것입니다.
2. Circle.ByCenterPointRadius: 여기서는 이전 단계와 동일한 입력으로 원 노드를 사용하겠습니다. 반지름 값의 기본값은 1.0이므로 원의 출력이 바로 표시됩니다. 따라서 점이 원점에서 얼마나 멀리 떨어져 있는지를 바로 확인할 수 있게 됩니다.

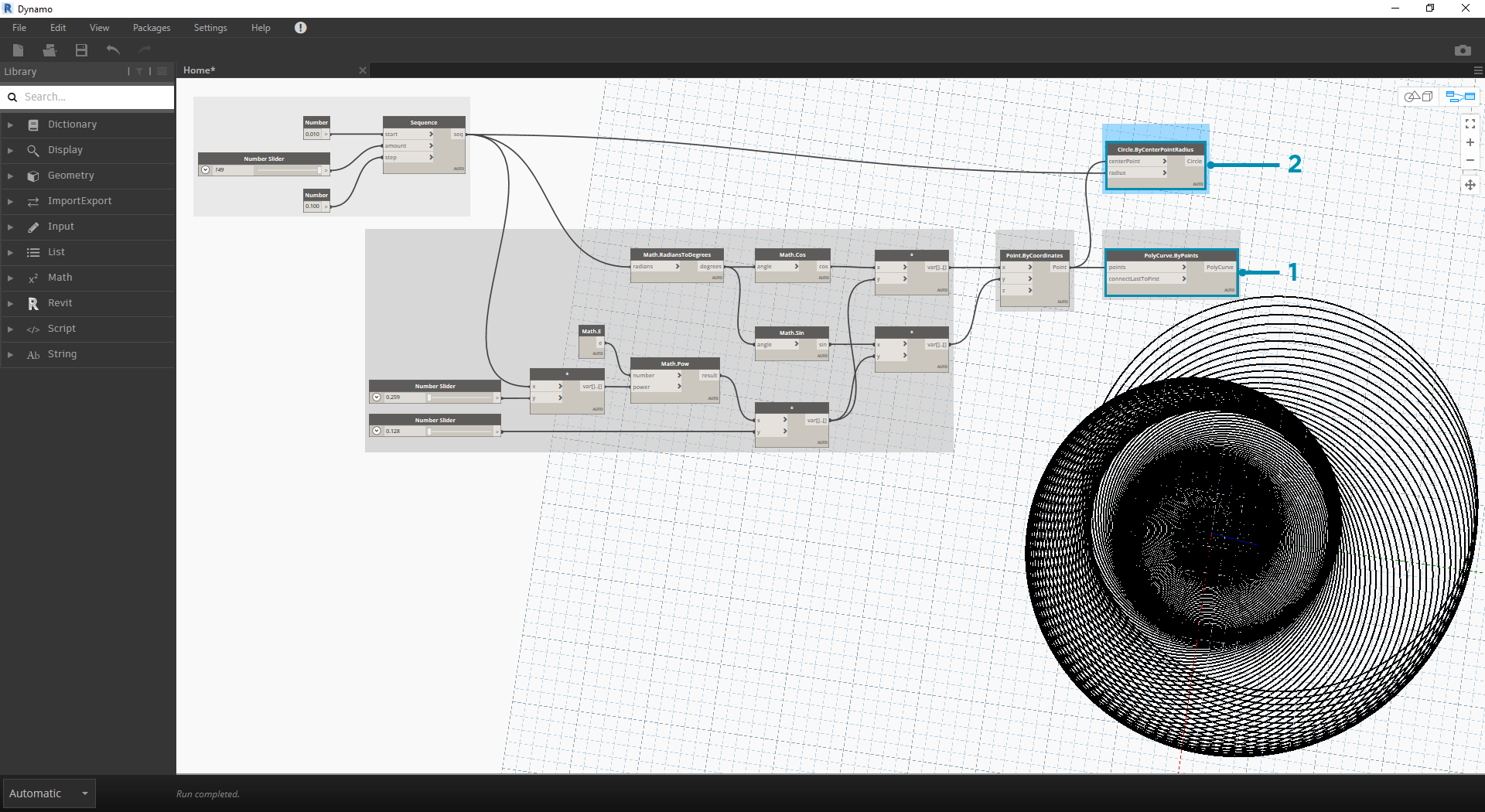
1. Circle.ByCenterPointRadius: 좀 더 동적인 원 배열을 작성하려면 원래 번호 시퀀스('t' 시퀀스)를 반지름 값에 연결합니다.
2. Number Sequence: 't'의 원래 배열입니다. 이를 반지름 값에 연결하면, 원 중심이 원점에서 계속 멀어지지만 원의 반지름은 증가하여 독특한 Fibonacci 원그래프가 작성됩니다. 이 그래프를 3D로 만들면 보너스 점수를 드리겠습니다.

Nautilus를 Phylorat 패턴으로

원형 Nautilus 쉘을 만들었으므로 파라메트릭 그리드로 건너뛰겠습니다. Fibonacci 나선에서 기본 회전을 사용하여 Fibonacci 그리드를 작성하면 해바라기 씨의 성장을 본뜬 결과가 모델링됩니다.

1. 다시 한번 이전 연습의 동일한 단계인 Point.ByCoordinates 노드로 나선형 점 배열 작성하기부터 시작해 보겠습니다.

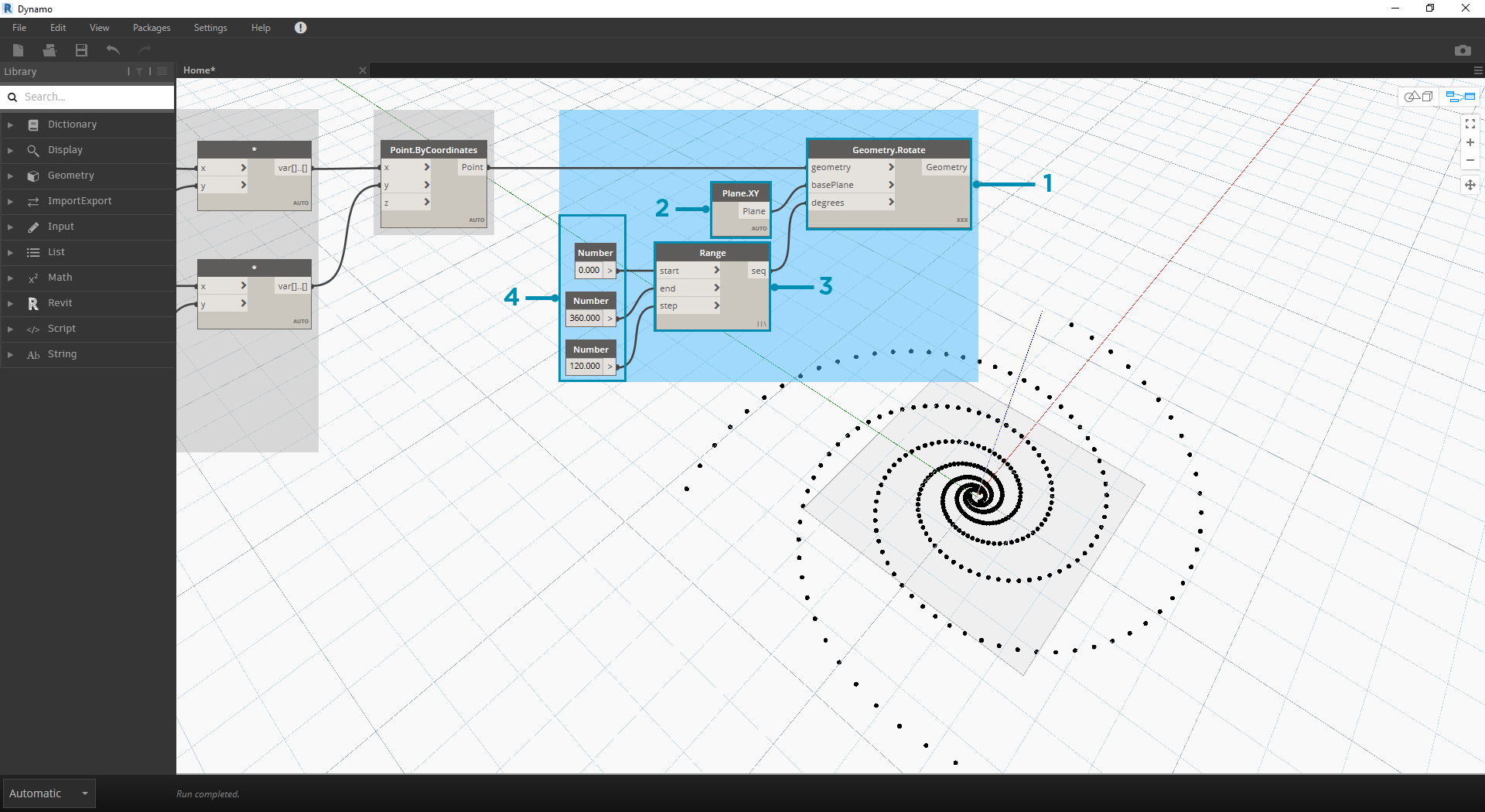
1. Geometry.Rotate: Geometry.Rotate 옵션에는 여러 가지가 있습니다. geometry,basePlane 및 degrees를 입력으로 사용하여 노드를 선택했는지 확인하십시오. Point.ByCoordinates를 형상 입력에 연결합니다.
2. Plane.XY: basePlane 입력에 연결합니다. 나선의 기준과 동일한 위치에 있는 원점을 중심으로 회전합니다.
3. Number Range: 각도 입력을 위해 여러 회전을 작성하려고 합니다. 이 작업은 숫자 범위 구성요소를 사용하여 빠르게 수행할 수 있습니다. 이 값을 degrees 입력에 연결합니다.
4. Number: 또한 숫자 범위를 정의하려면 캔버스에 세로로 세 개의 숫자 노드를 추가합니다. 위에서 아래로 0.0,360.0, 및 120.0 값을 각각 지정합니다. 그러면 나선이 회전하게 됩니다. 3개의 숫자 노드를 해당 노드에 연결한 후 Number Range 노드의 출력 결과를 확인합니다.

처음에는 출력이 소용돌이와 비슷합니다. Number Range 매개변수 중 일부를 조정하고 결과가 어떻게 달라지는지 확인해 보겠습니다.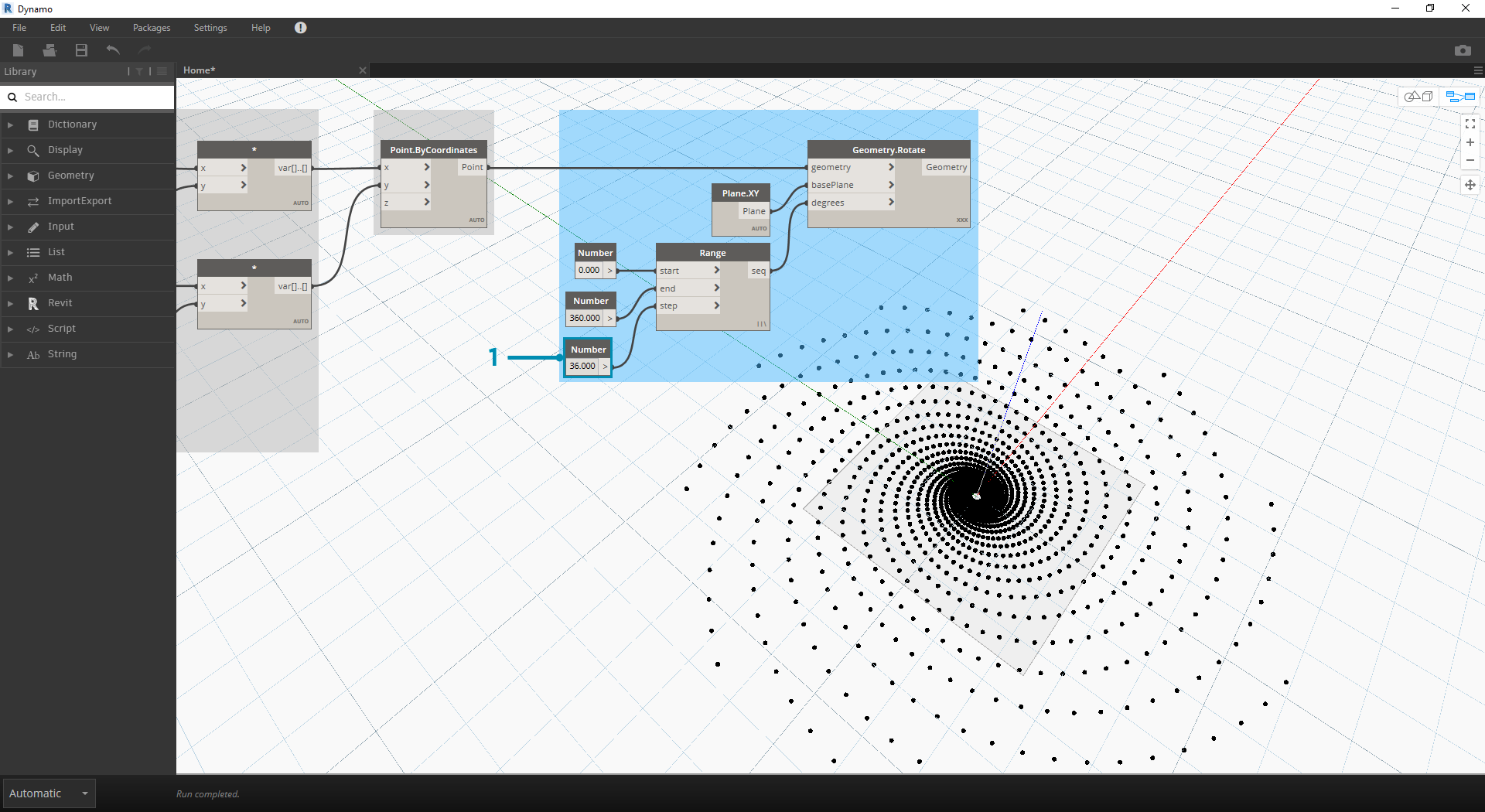

1. Number Range 노드의 단계 크기를 120.0에서 36.0으로 변경합니다. 이렇게 하면 더 많은 회전이 작성되므로 그리드가 더 조밀해집니다.

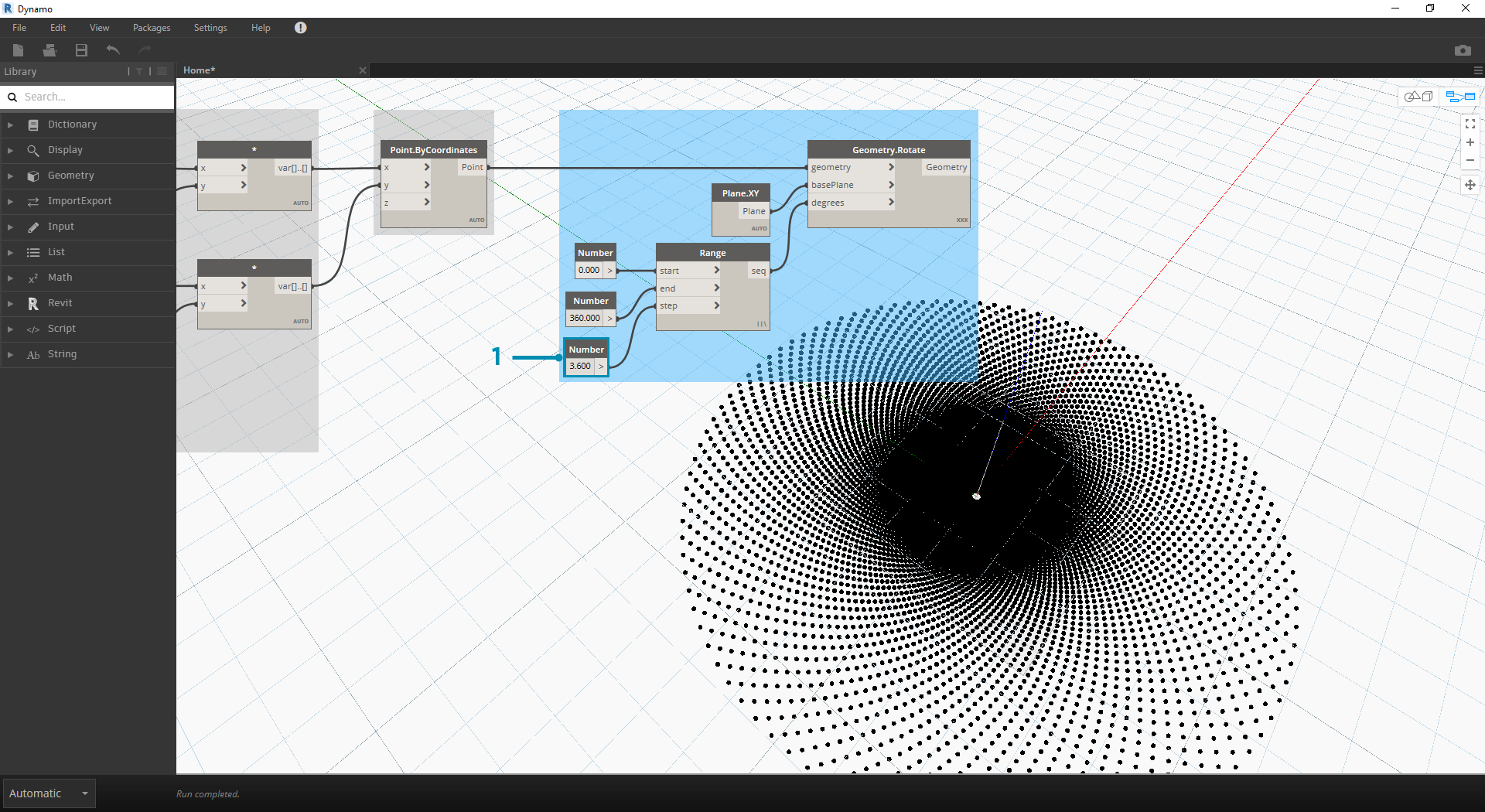
1. Number Range 노드의 단계 크기를 36.0에서 3.6으로 변경합니다. 그러면 훨씬 더 조밀한 그리드가 표시되고 나선의 방향은 불명확해집니다. 해바라기가 작성된 것입니다.