コード ブロック関数
関数は Code Block ノード内で作成することができ、Dynamo 定義の任意の場所から呼び出すことができます。これにより、パラメトリック ファイル内に新しいコントロール レイヤーが追加されます。Code Block ノードは、テキストベースのカスタム ノードとしてみなすことができます。この場合、「親」コード ブロックに簡単にアクセスすることができます。親コード ブロックは、グラフ上の任意の場所に配置することができます。ワイヤは必要ありません。
親
最初の行に、キーワードの「def」と関数名を続けて入力し、入力データの名前を括弧で囲んで記述します。関数の本文を定義する場合は、波括弧 {} を使用します。値を返す場合は、「return =」を指定します。関数を定義する Code Block ノードは他の Code Block ノードから呼び出されるため、入力ポートと出力ポートはありません。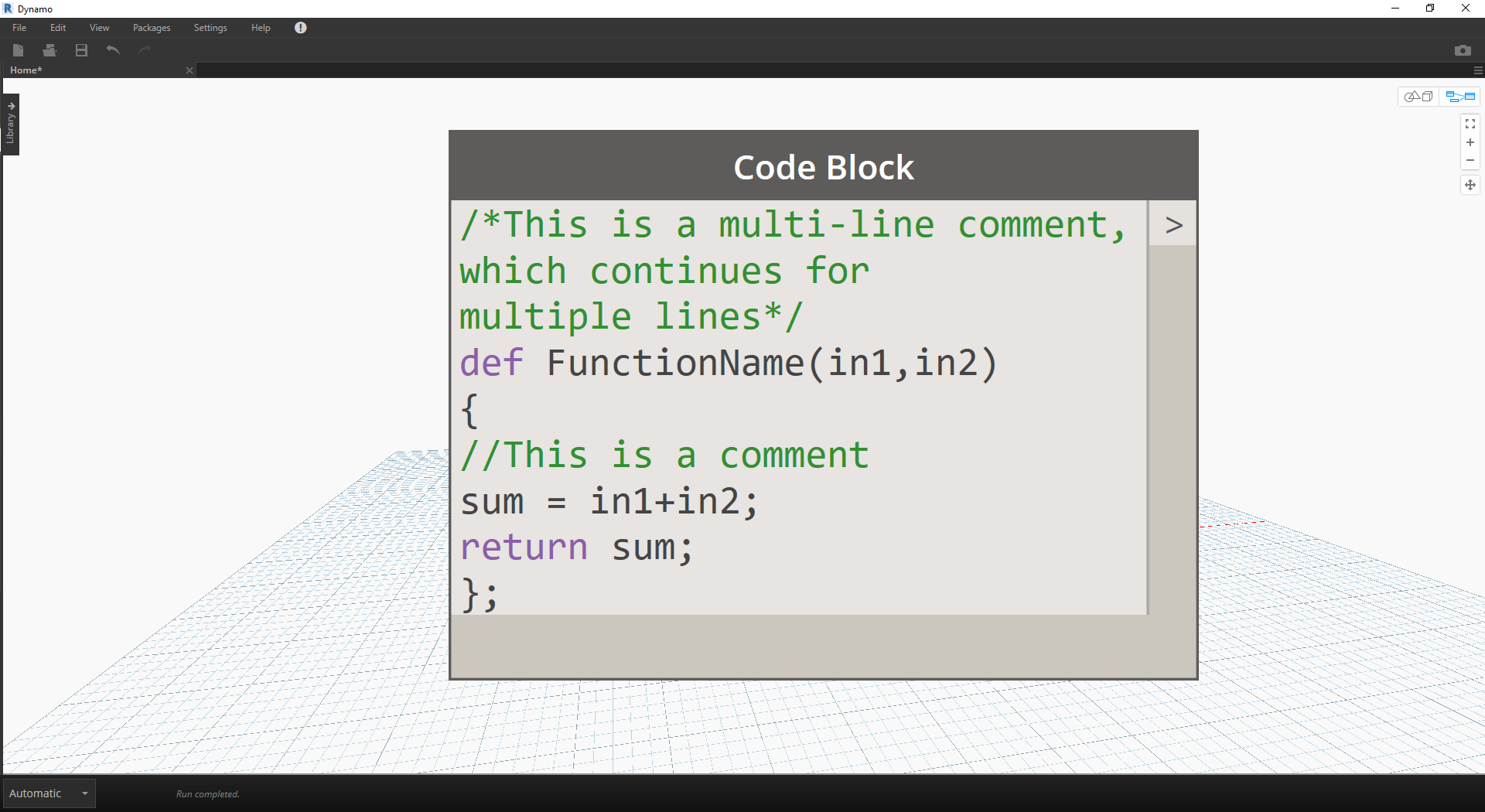
/*This is a multi-line comment,
which continues for
multiple lines*/
def FunctionName(in1,in2)
{
//This is a comment
sum = in1+in2;
return sum;
};
子
関数を呼び出すには、同じファイル内で別の Code Block ノードを使用して、呼び出す関数の名前と、親 Code Block ノードで定義されているものと同じ数の引数を指定します。これは、ライブラリ内に用意されているノードと同様に動作します。
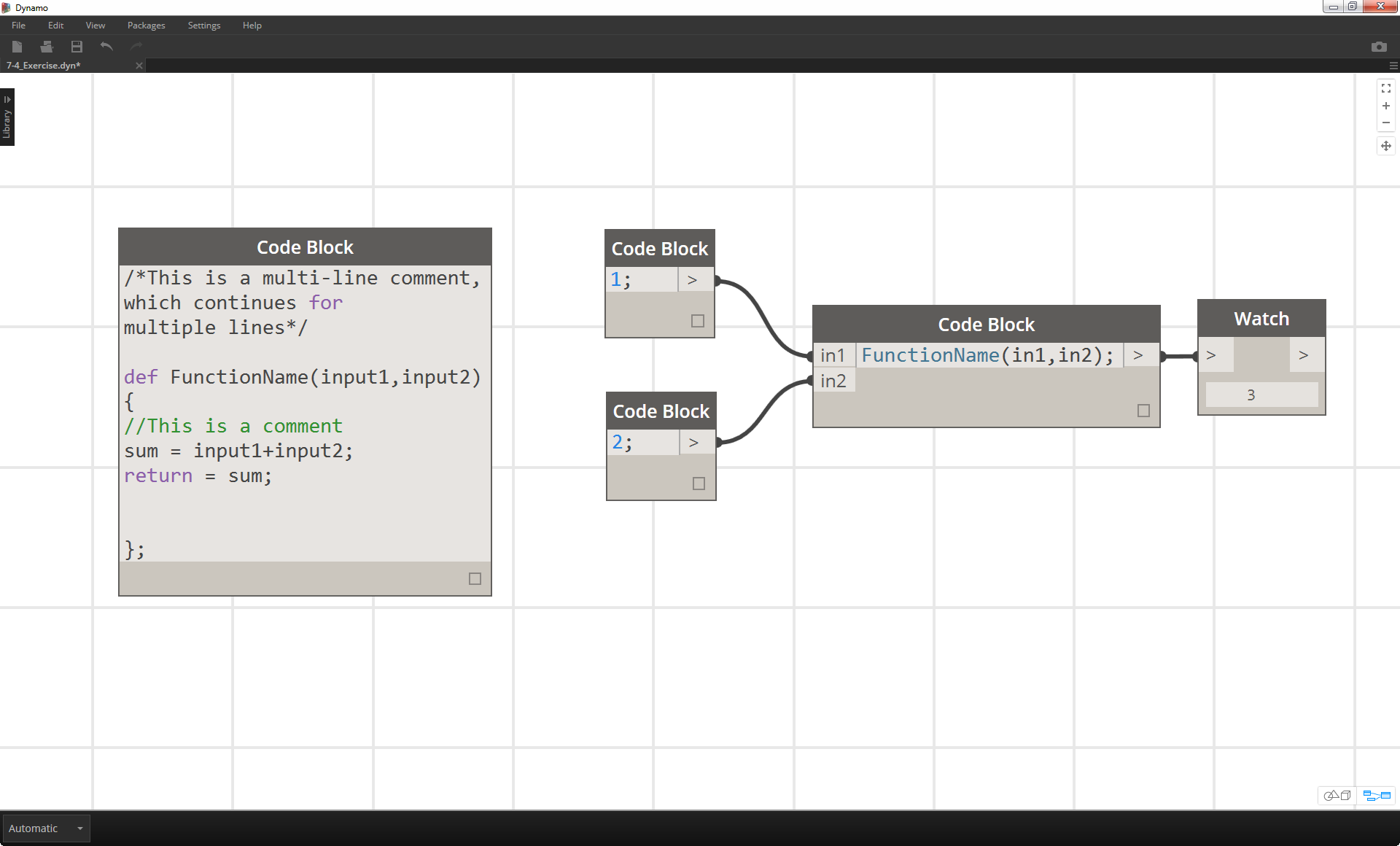
FunctionName(in1,in2);
演習
この演習に付属しているサンプル ファイルをダウンロードしてください(右クリックして[名前を付けてリンク先を保存]を選択)。すべてのサンプルファイルの一覧については、付録を参照してください。Functions_SphereByZ.dyn
この演習では、点の入力リストから球体を生成する一般的な定義を作成します。これらの球体の半径は、各点の Z プロパティによってコントロールされます。
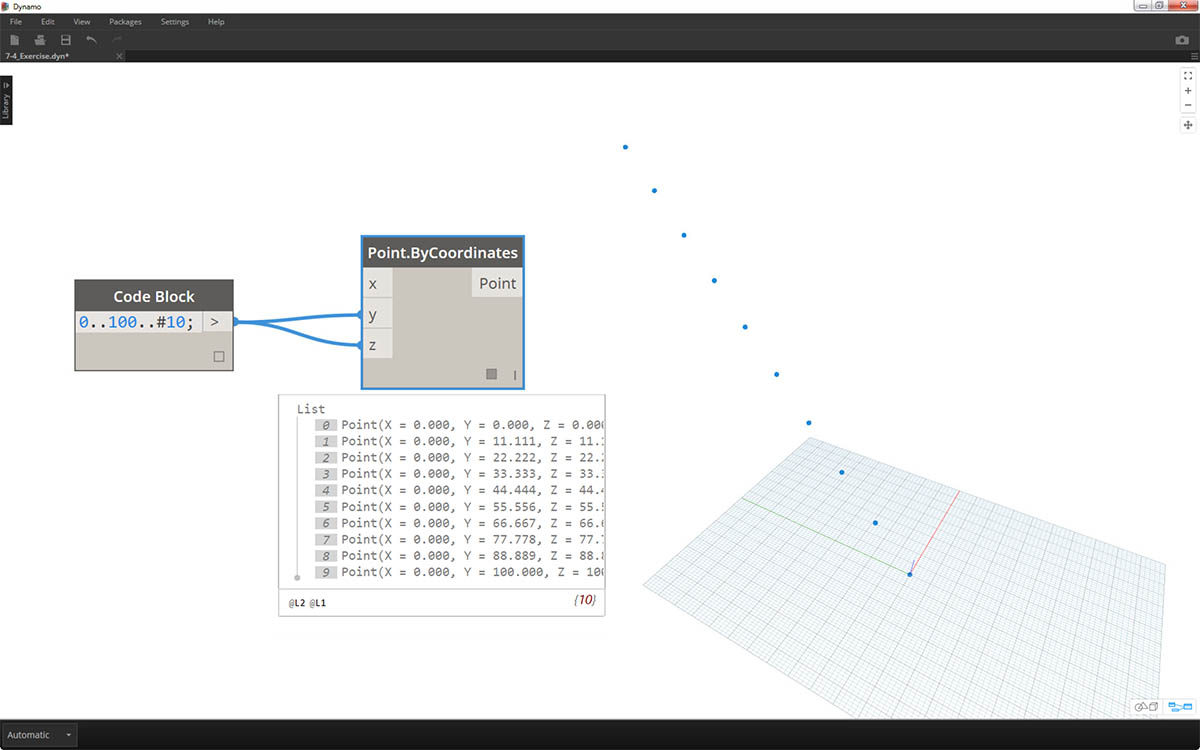
最初に、0 から 100 までの範囲内で 10 個の数値を作成しましょう。これらの数値を Point.ByCoordinates ノードに接続し、斜線を作成します。
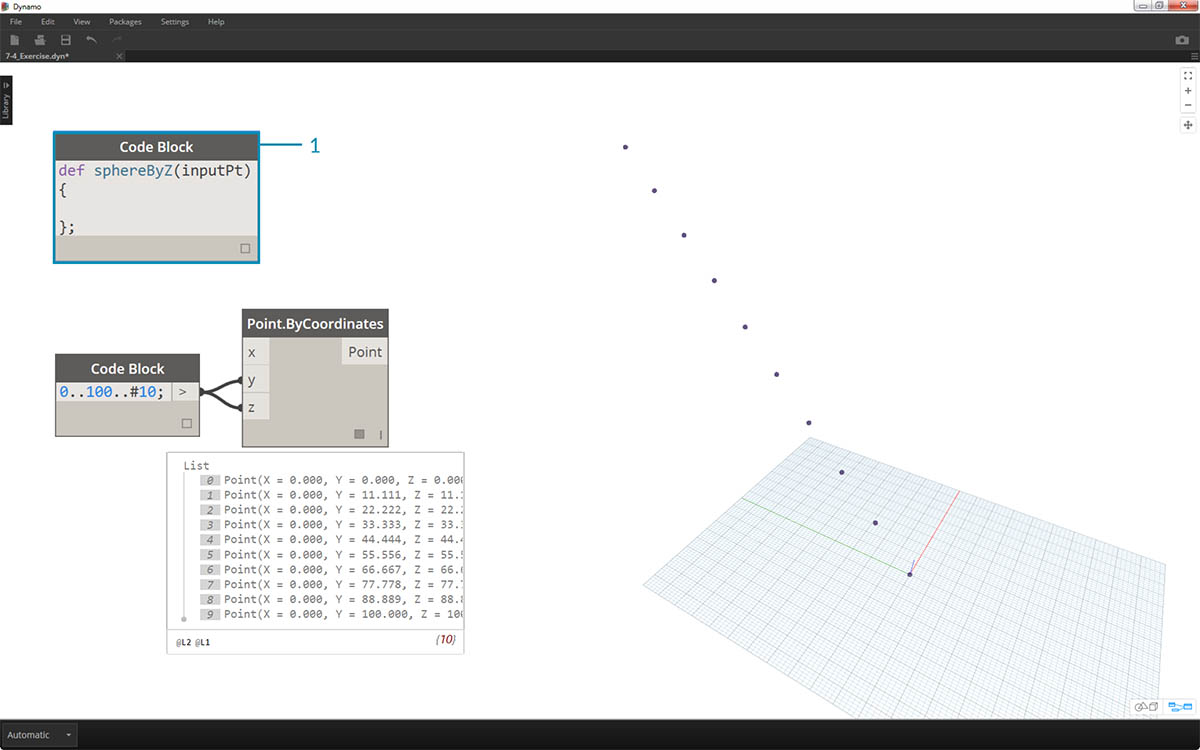
- Code Block ノードを作成し、コード行を使用して定義を開始します。
def sphereByZ(inputPt){ };
inputPt は、関数をコントロールする点を表す名前です。 この時点では、この関数はまだ機能しませんが、これ以降の手順でこの関数を設定していきます。
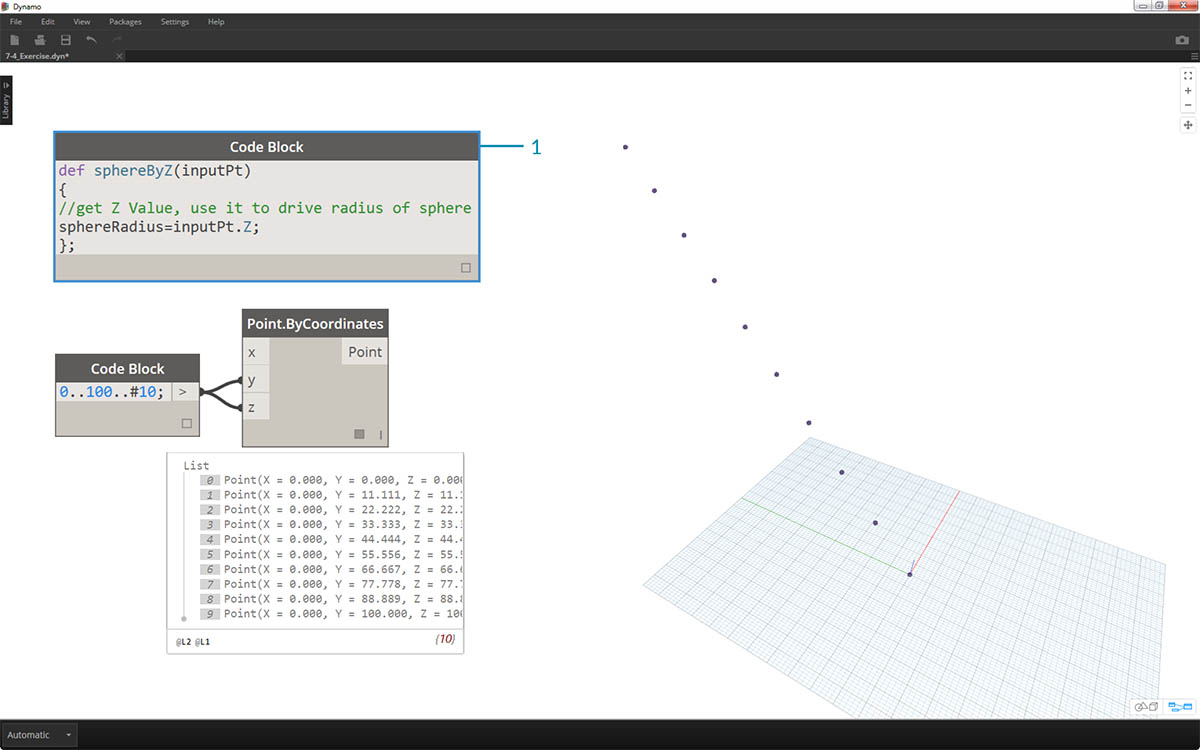
- Code Block ノードを使用して、この関数にコメントと sphereRadius 変数を入力します。この変数により、各点の Z 位置のクエリーが実行されます。 inputPt.Z はメソッドであるため、引数を指定するための括弧は必要ありません。 これは既存の要素のプロパティのクエリーであるため、入力は必要ありません。
def sphereByZ(inputPt,radiusRatio) { //get Z Value, use it to drive radius of sphere sphereRadius=inputPt.Z; };
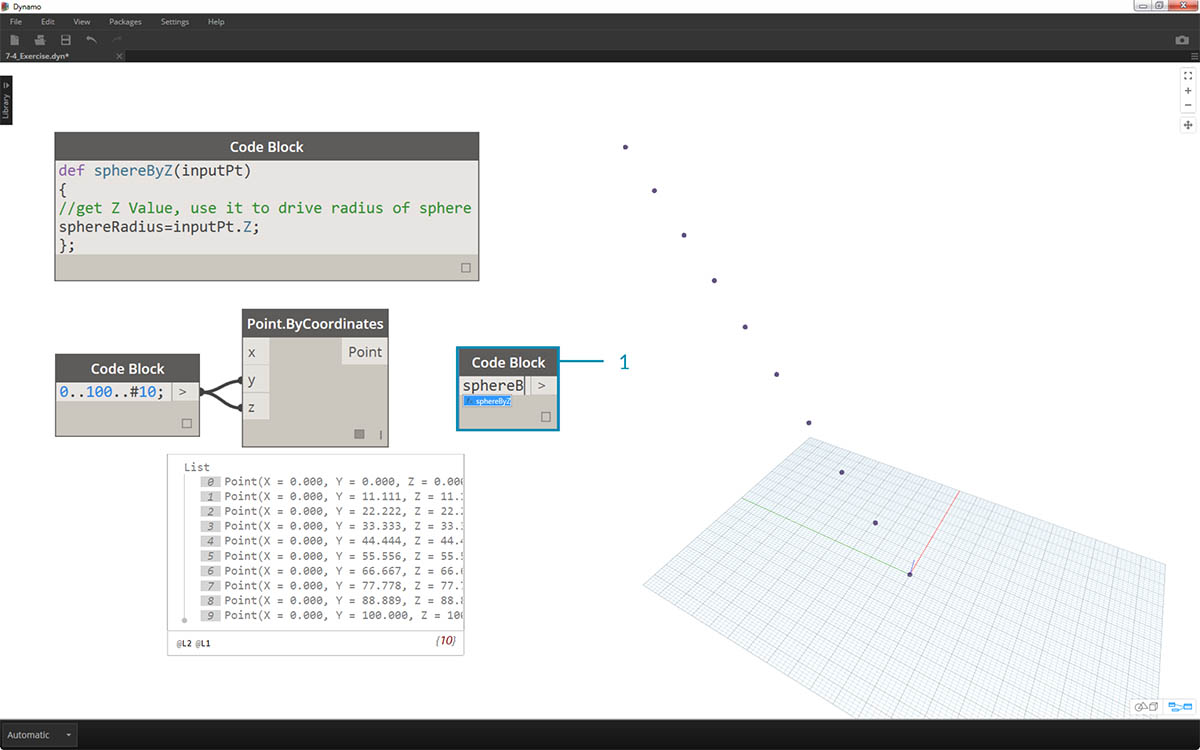
- ここで、別の Code Block ノードで作成した関数を呼び出してみましょう。 キャンバスをダブルクリックして新しい Code Block ノードを作成し、sphereB と入力すると、既に定義されている sphereByZ 関数が候補として表示されます。 これにより、前の手順で作成した関数が IntelliSense ライブラリに追加されていることがわかります。
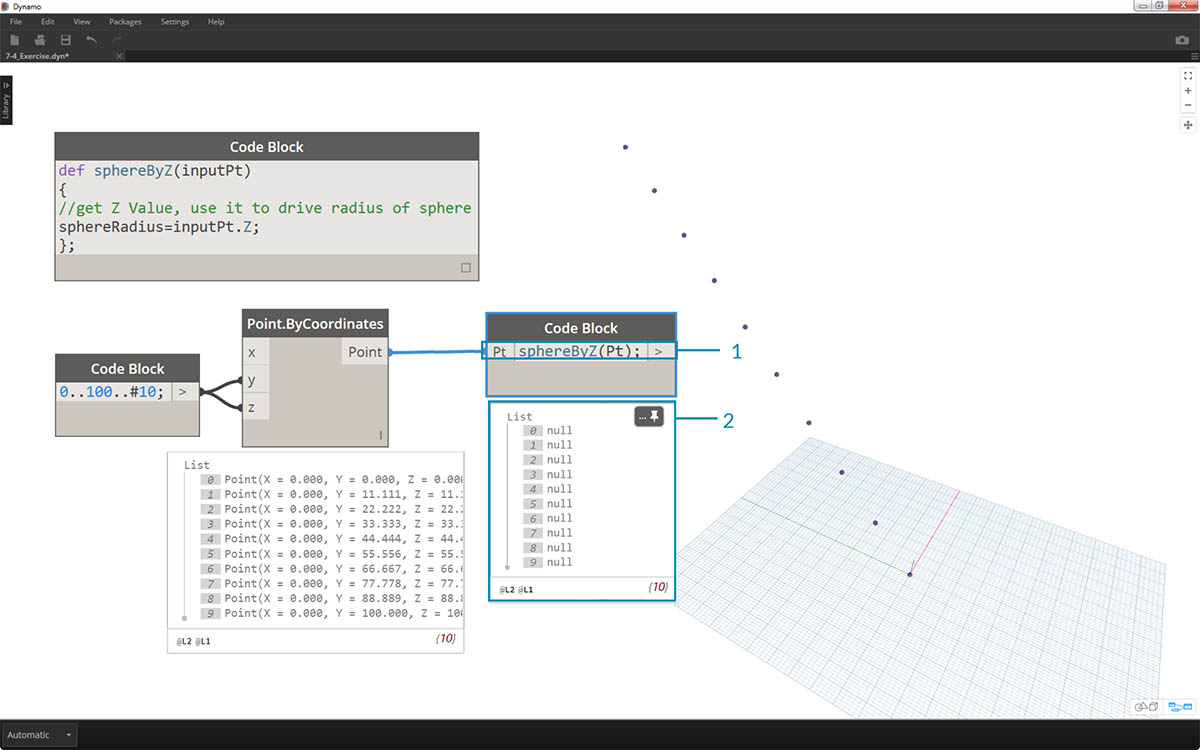
- 関数を呼び出して Pt という変数を作成して、前の手順で作成した点を接続します。
sphereByZ(Pt)
- 出力されたリストを確認すると、値がすべて NULL になっていることがわかります。なぜでしょうか。これは、この関数を定義するときに sphereRadius 変数は計算しましたが、この関数が何を出力として返すのかを定義しなかったためです。** これについては、次の手順で修正します。
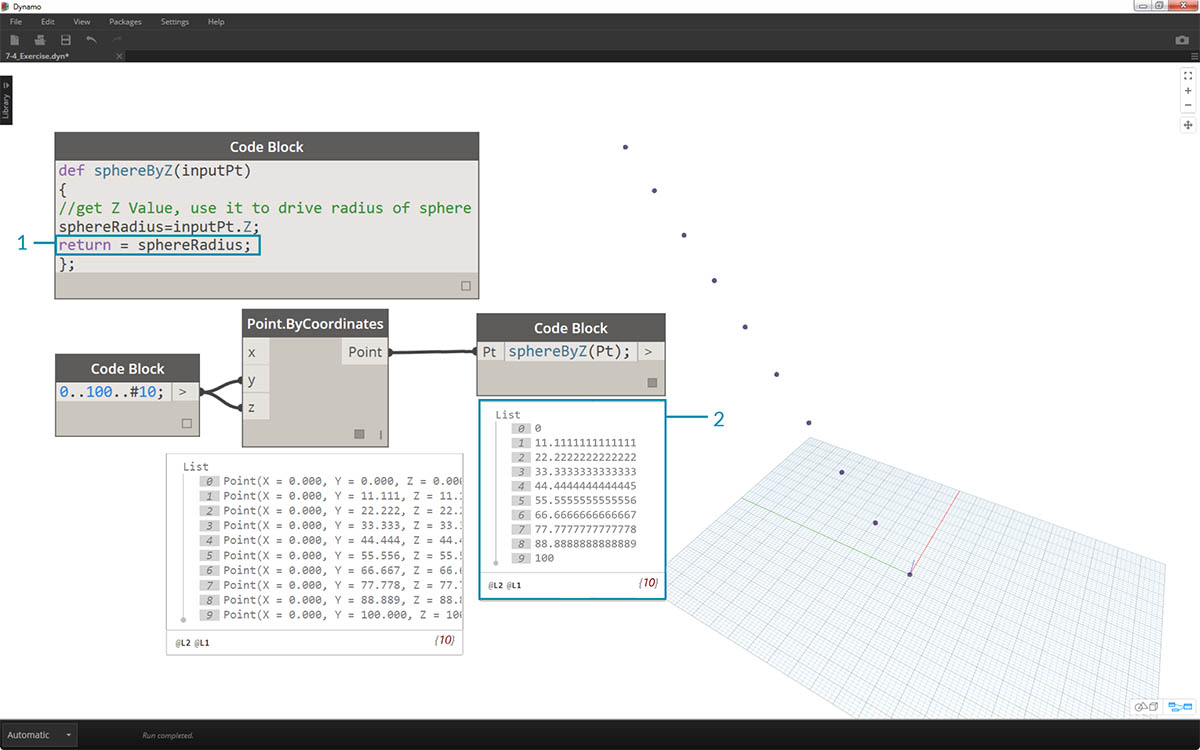
- sphereByZ 関数に
return = sphereRadiusというコード行を追加して、関数の出力を定義する必要があります。これは重要な手順です。- Code Block ノードの出力は、各点の Z 座標です。
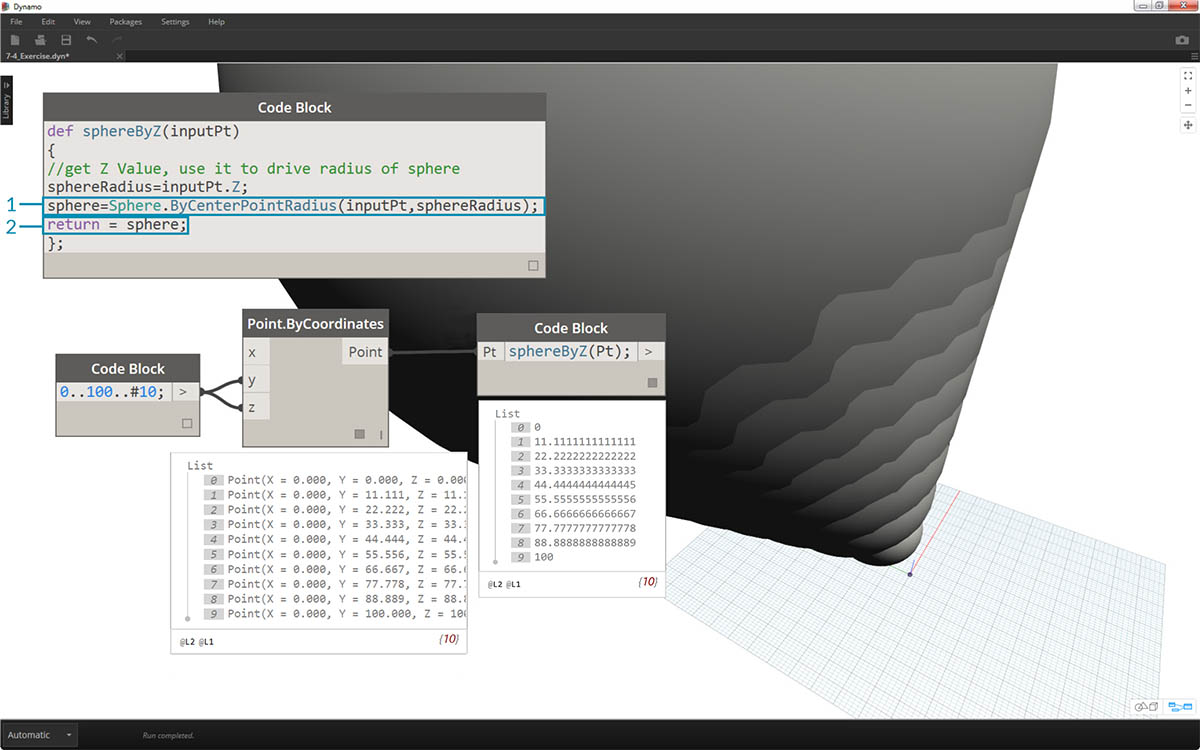
親関数を編集して、実際に球体を作成してみましょう。
- 最初に、
sphere=Sphere.ByCenterPointRadius(inputPt、sphereRadius);というコード行で球体を定義します。- 次に、戻り値が sphereRadius から sphere となるように、
return=sphere;と記述します。 これで、Dynamo プレビューに非常に大きな球体が表示されます。
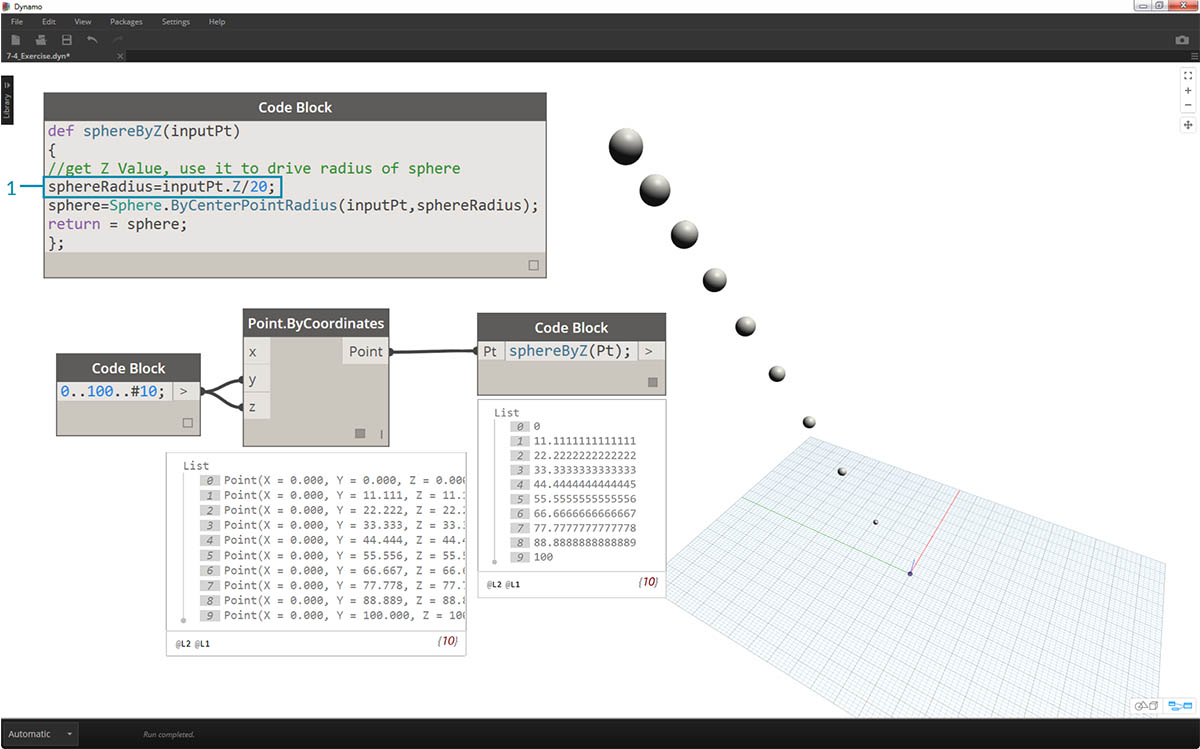
sphereRadius=inputPt.Z/20;という除数を追加して sphereRadius の値を更新し、球体のサイズを調整します。 これで、各球体が離れて表示され、半径と Z 値との関係がわかるようになります。
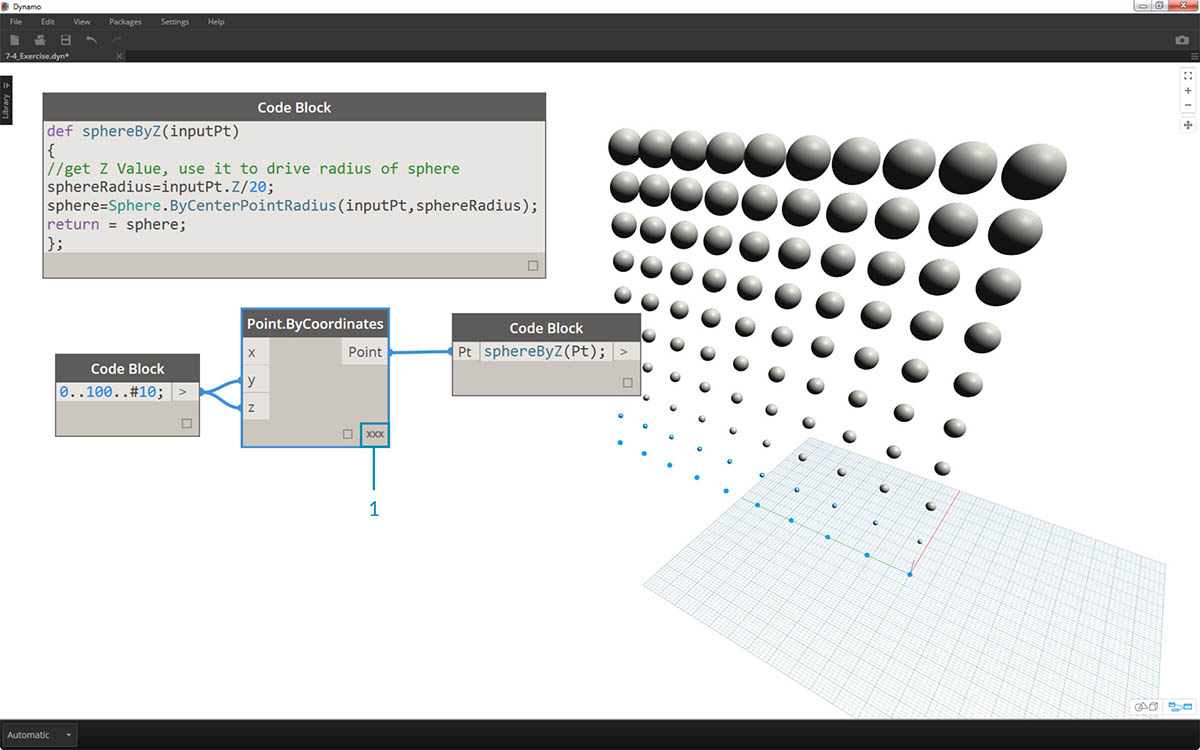
- Point.ByCoordinates ノードでレーシングを[最短リスト]から[直積]に変更して、点のグリッドを作成します。 sphereByZ 関数により、すべての点で Z 値に基づいた半径の円が作成されます。
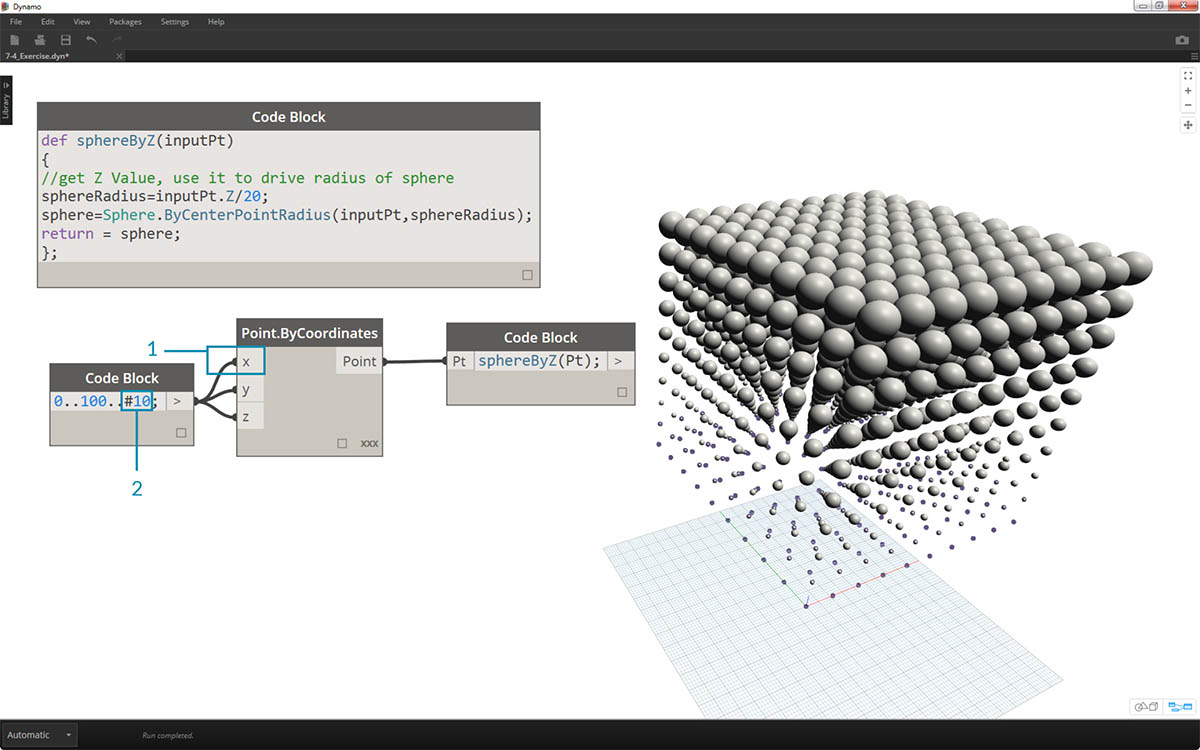
- 次に、Point.ByCoordinates ノードの X 入力に元の数値のリストを接続してみます。 この操作により、球体によって構成される立方体が作成されます。
- 注: この処理に時間がかかる場合は、#10 を #5 などの値に変更してください。
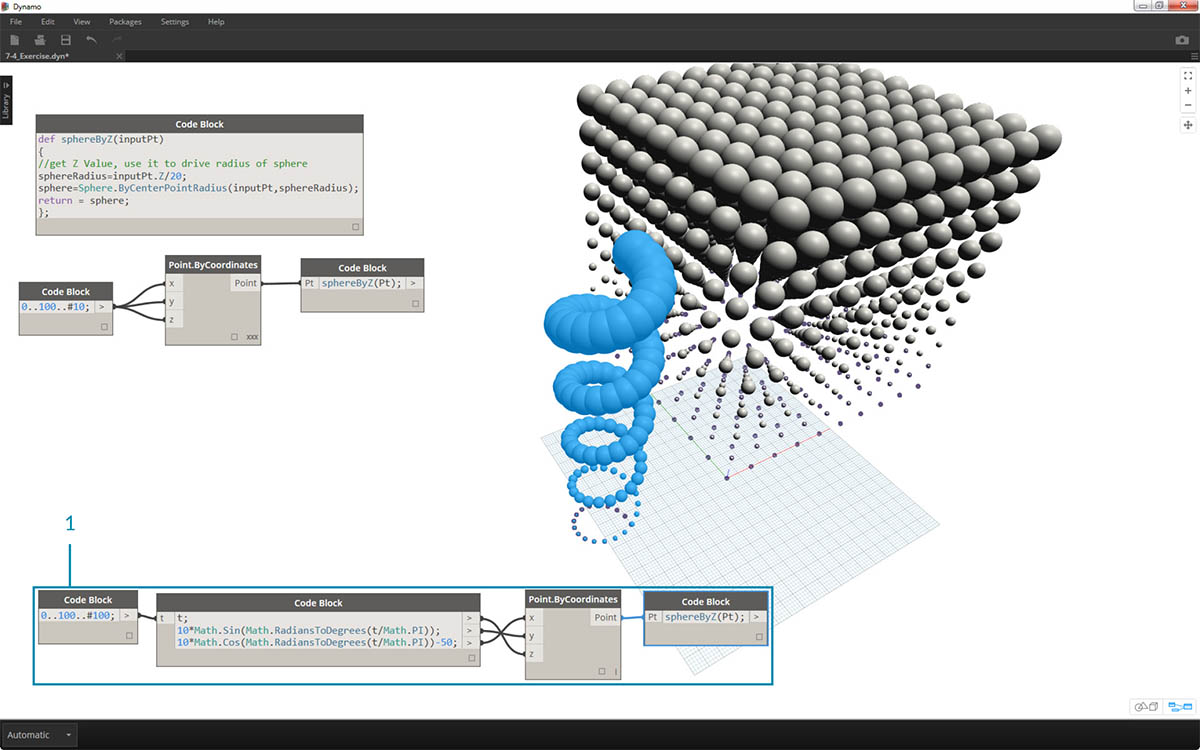
- ここで作成した sphereByZ 関数は汎用的な関数であるため、前の演習で作成したらせん構造を呼び出して、この関数を適用することができます。
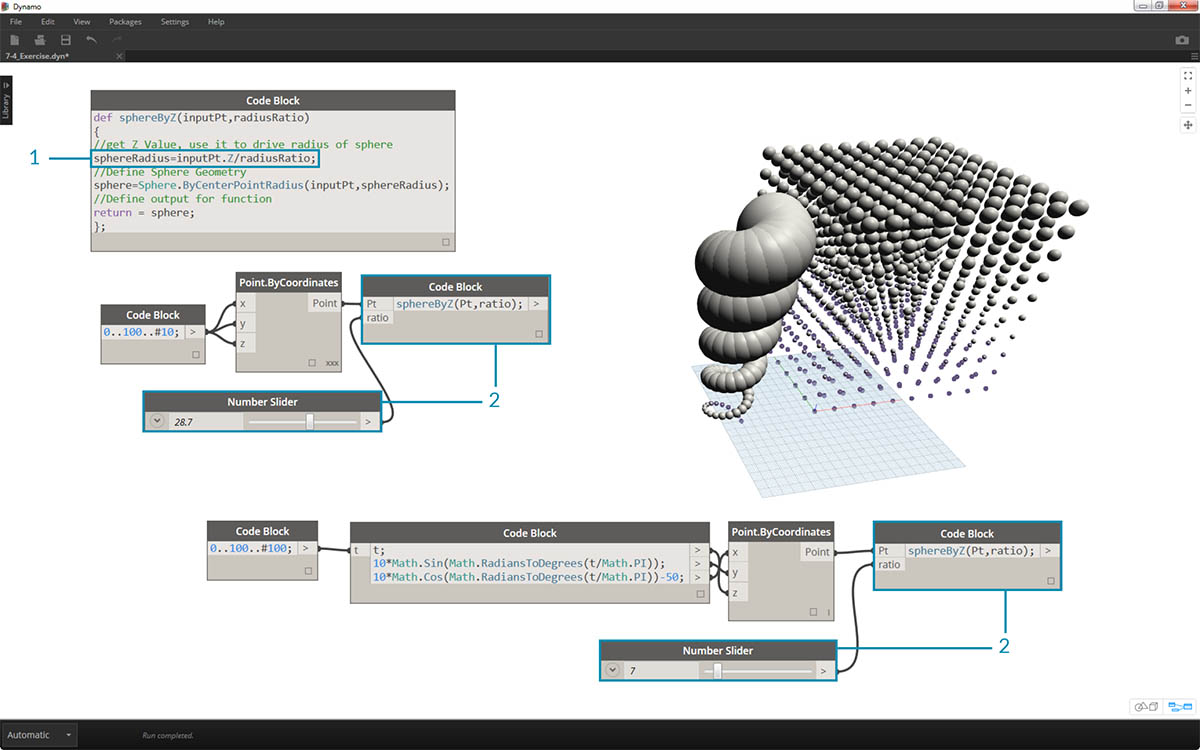
最後に、半径の比をユーザ設定のパラメータでコントロールしてみましょう。これを行うには、関数に対して新しい入力を作成し、除数の 20 をパラメータで置き換える必要があります。
- sphereByZ 関数の定義を、次のように更新します。
def sphereByZ(inputPt,radiusRatio) { //get Z Value, use it to drive radius of sphere sphereRadius=inputPt.Z/radiusRatio; //Define Sphere Geometry sphere=Sphere.ByCenterPointRadius(inputPt,sphereRadius); //Define output for function return sphere; };
sphereByZ(Pt,ratio);のように、子の Code Block ノードの入力に ratio 変数を追加して更新します。次に、新しく作成した Code Block ノードの入力に Number Slider ノードを接続し、半径の比に基づいて半径のサイズを変更します。